Как измеряется площадь: Ошибка 403 — доступ запрещён

Единицы измерения площадей. Свойства площадей / Геометрия / Справочник по математике 5-9 класс

1. Главная
2. Справочники
3. Справочник по математике 5-9 класс
4. Геометрия
5. Единицы измерения площадей. Свойства площадей

Измерение площадей

Для измерения площадей используют такие единицы измерения:

квадратный сантиметр, квадратный дециметр, квадратный метр, квадратный километр

Вспомните, что квадрат — это прямоугольник, у которого все стороны равны

---

Квадратный сантиметр – это площадь квадрата со стороной в 1 см    

---

Квадратный дециметр – это площадь квадрата со стороной в 1 дм

 

---

Квадратный метр – это площадь квадрата со стороной в 1 м

---

Для измерения больших площадей используют квадратный километр – это площадь квадрата, сторона которого равна 1 км

Слова «квадратный километр» сокращенно при числе записывают так – 1 км², 2 км², 130 км².

В квадратных километрах измеряют, например, площади городов (площадь Москвы 1091 км²)

Обозначают площадь заглавной буквой латинского алфавита S

---

Площади полей измеряют в гектарах (га).

Гектар — это площадь квадрата со стороной 100 м.

Значит, 1 га равен 100 ∙ 100 квадратных метров, то    есть 1 га = 10 000 м².

Площади небольших участков земли измеряют в арах (а).

Ар (сотка) — площадь квадрата со стороной 10 м.

Значит, 1 а  =  100 м².

---

Так как 1 дм = 10 см, то в 1 дм² содержится 10 · 10 квадратных сантиметров, то есть 1 дм² = 100 см².

Так же устанавливаем, что 1 м² = 100 дм².

Так как 1 м = 100 см, то в 1 м² содержится 100 ∙  100 квадратных сантиметров, то есть 1 м² = 10 000 см².

Измерить площадь — значит подсчитать, сколько единичных квадратов в ней помещается.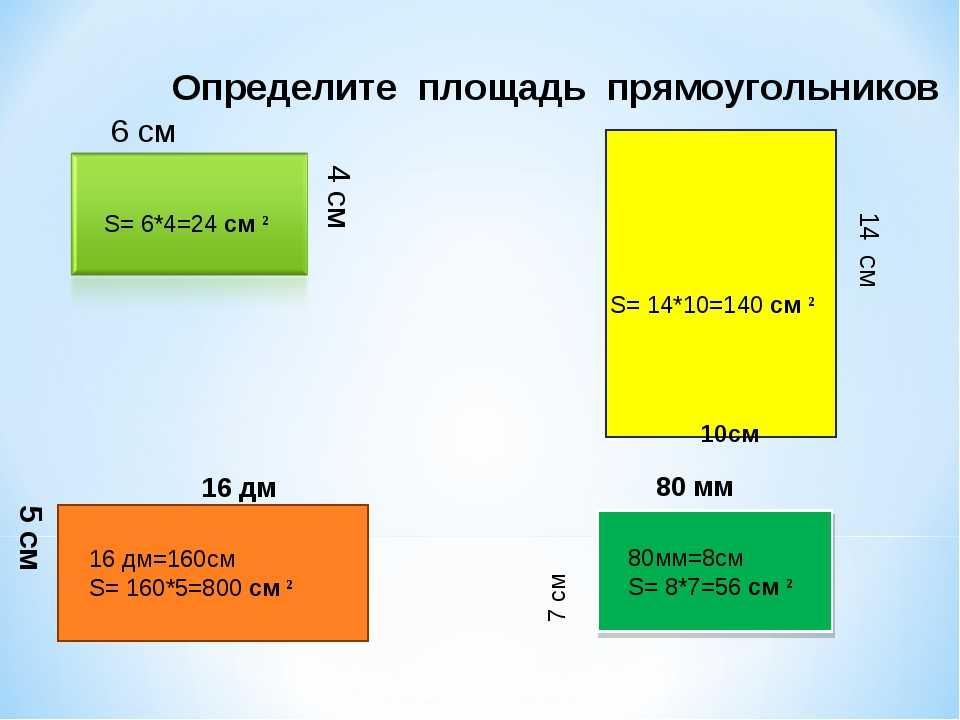

Соотношения между единицами измерения площадей 

---

Если длина и ширина прямоугольника выражены, например, в метрах, то его площадь выражается в квадратных метрах.

Если длина и ширина прямоугольника измерены в разных единицах, то их надо выразить в одних единицах.

---

Свойства площадей

1. Равные фигуры имеют равные площади (равные фигуры при наложении совпадут).
2. Площадь фигуры равна сумме площадей фигур, из которых она состоит.

Советуем посмотреть:

Отрезок

Ломаная

Четырехугольники

Прямоугольник, его периметр и площадь. Ось симметрии фигуры

Квадрат. Периметр и площадь квадрата.

Многоугольники. Правильные многоугольники. Равенство фигур.

Плоскость

Прямая

Луч

Шкалы и координаты

Прямоугольный параллелепипед. Пирамида.

Объем прямоугольного параллелепипеда

Куб. Площадь поверхности куба

Куб. Объем куба

Угол. Обозначение углов

Прямой и развернутый угол

Чертежный треугольник

Измерение углов. Транспортир. Виды углов

Треугольник и его виды

Окружность, круг, шар

Цилиндр, конус

Отрезок-xx

Геометрия

Правило встречается в следующих упражнениях:

5 класс

Задание 710, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 749, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 755, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 756, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 758, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 759, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 780, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 4, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1

Номер 581, Мерзляк, Полонский, Якир, Учебник

Номер 7, Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 578, Мерзляк, Полонский, Якир, Учебник

Номер 595, Мерзляк, Полонский, Якир, Учебник

Задание 138, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 465, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 768, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 800, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 833, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 857, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1586, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 3, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1

7 класс

Номер 181, Мерзляк, Полонский, Якир, Учебник

---

Периметр и площадь геометрических фигур

• Периметр
• Площадь
• Таблица перевода квадратных единиц

Существует много плоских геометрических фигур: точка, линия (прямая или кривая), отрезок, угол, ломаная и т. д.:

Если внимательно посмотреть на все эти фигуры, то можно выделить две из них, которые образованы замкнутыми линиями (окружность и треугольник). Эти фигуры имеют своего рода границу, отделяющую то что находится внутри, от того что находится снаружи. То есть граница делит плоскость на две части: внутреннюю и внешнюю область относительно фигуры, к которой она относится:

Периметр

Периметр – это замкнутая граница плоской геометрической фигуры, отделяющая её внутреннюю область от внешней.

Периметр есть у любой замкнутой геометрической фигуры:

На рисунке периметры выделены красной линией. Обратите внимание, что периметр окружности часто называют длиной.

Периметр измеряется в единицах измерения длины:  мм,  см,  дм,  м,  км.

У всех многоугольников нахождение периметра сводится к сложению длин всех сторон, то есть периметр многоугольника всегда равен сумме длин его сторон. При вычислении периметр часто обозначают большой латинской буквой P:

Площадь

Площадь – это часть плоскости, занимаемая замкнутой плоской геометрической фигурой.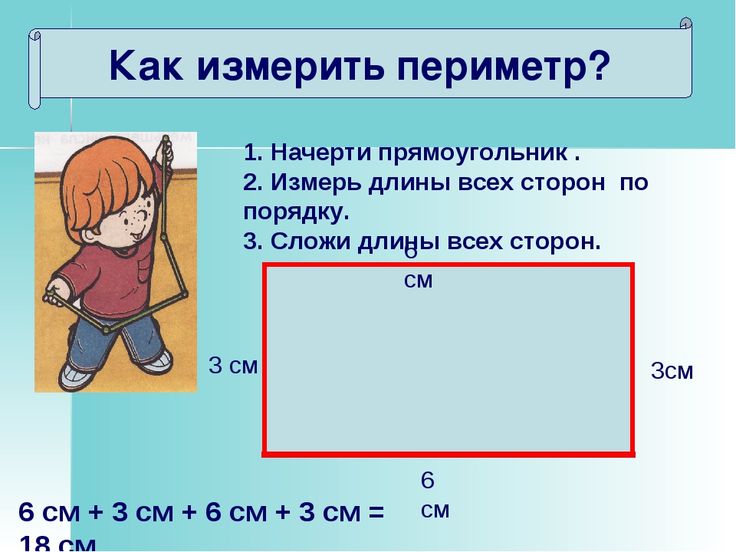

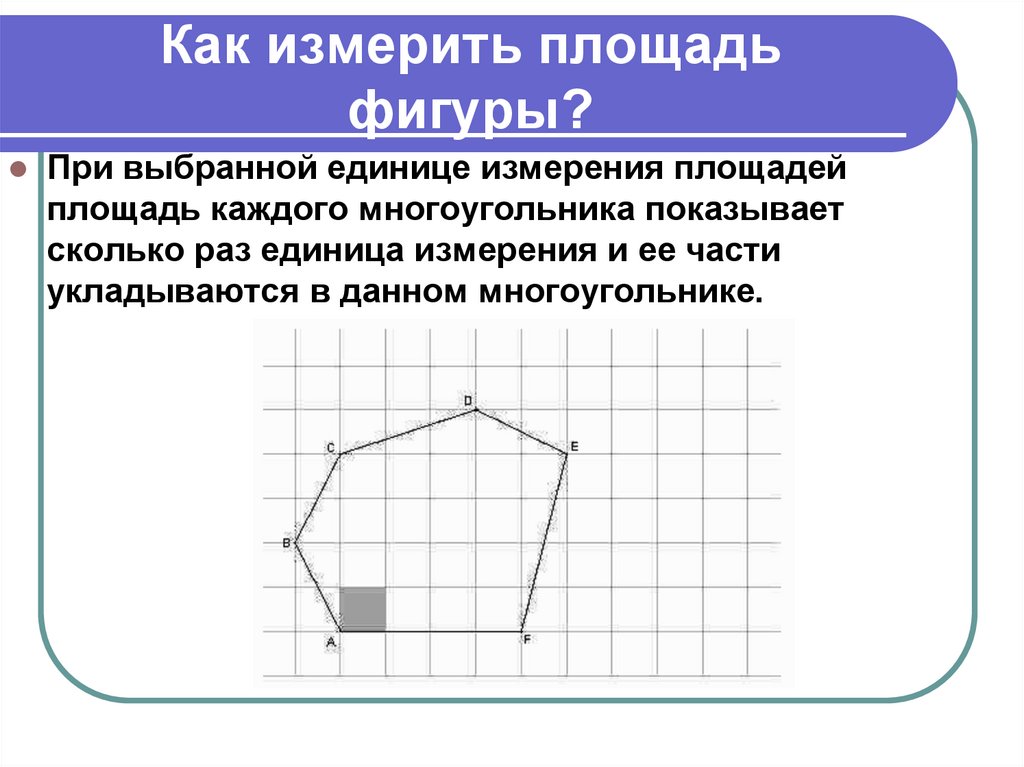
Любая плоская замкнутая геометрическая фигура имеет определённую площадь. На чертежах площадью геометрических фигур является внутренняя область, то есть та часть плоскости, которая находится внутри периметра.

Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Обычно за единицу измерения площади принимается квадрат, у которого сторона равна единице измерения длины: миллиметру, сантиметру, метру и т. д.

На рисунке изображён квадратный сантиметр. Квадратный сантиметр — квадрат, у которого каждая сторона имеет длину 1 см:

Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся:  мм²,  см²,  м²,  км²  и т. д.

Таблица перевода квадратных единиц

	мм2	см2	дм2	м2	ар (сотка)	гектар (га)	км2
мм2	1 мм2	0,01 см2	10-4 дм2	10-6 м2	10-8 ар	10-10 га	10-12 км2
см2	100 мм2	1 см2	0,01 дм2	10-4 м2	10-6 ар	10-8 га	10-10 км2
дм2	104 мм2	100 см2	1 дм2	0,01 м2	10-4 ар	10-6 га	10 -8 км2
м2	106 мм2	104 см2	100 дм2	1 м2	0,01 ар	10-4 га	10-6 км2
ар	108 мм2	106 см2	104 дм2	100 м2	1 ар	0,01 га	10-4 км2
га	1010 мм2	108 см2	106 дм2	104 м2	100 ар	1 га	0,01 км2
км2	1012 мм2	1010 см2	108 дм2	106 м2	104 ар	100 га	1 км2

104 = 10 000	10-4 = 0,000 1
106 = 1 000 000	10-6 = 0,000 001
108 = 100 000 000	10-8 = 0,000 000 01
1010 = 10 000 000 000	10-10 = 0,000 000 000 1
1012 = 1 000 000 000 000	10-12 = 0,000 000 000 001

Что такое площадь? Определение, площадь фигур Формула

Площадь – это площадь, занимаемая двухмерной фигурой. Другими словами, это величина, измеряющая количество единичных квадратов, покрывающих поверхность замкнутой фигуры. Стандартной единицей площади являются квадратные единицы, которые обычно представляются как квадратные дюймы, квадратные футы и т. д. Давайте научимся вычислять площадь различных геометрических фигур с помощью примеров и практических вопросов.

1.	Что такое площадь?
2.	Как рассчитать площадь?
3.	Площадь геометрических фигур — Формула
4.	Часто задаваемые вопросы по Зоне

Что такое площадь?

Слово «площадь» означает свободную поверхность. Площадь фигуры вычисляется с помощью ее длины и ширины. Длина одномерна и измеряется в таких единицах, как футы (футы), ярды (ярды), дюймы (дюймы) и т. д. Однако площадь формы является двумерной величиной.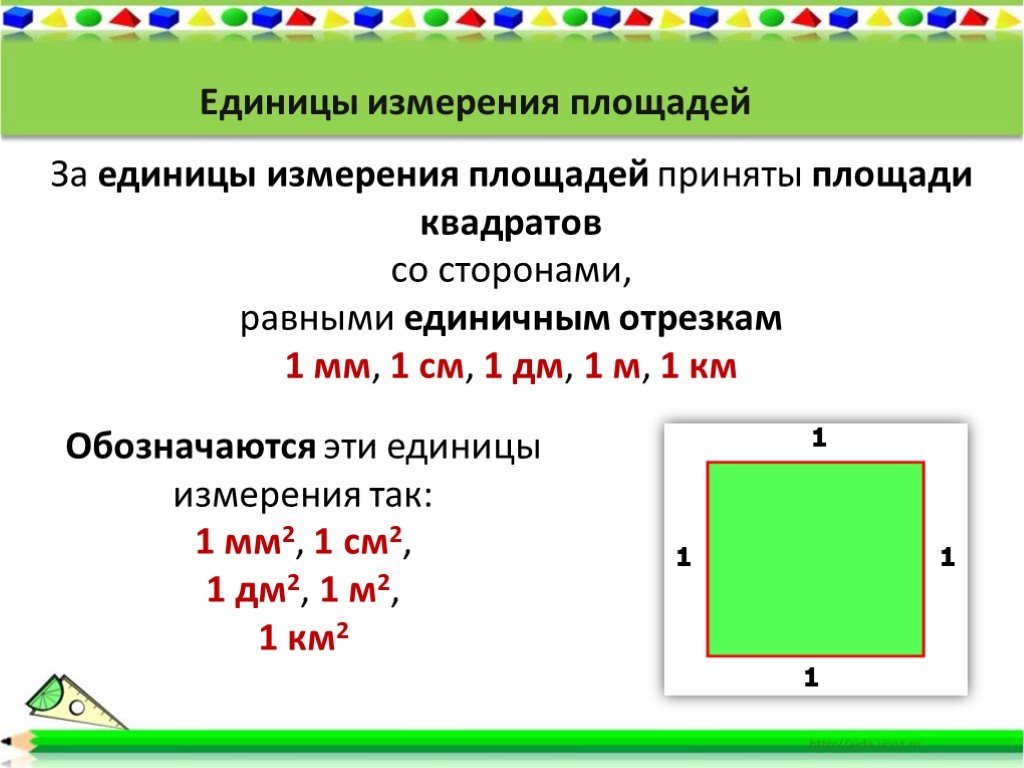

Следовательно, он измеряется в квадратных единицах, таких как квадратные дюймы или (в ² ), квадратных футов или (ft ² ), квадратных ярдов или (yd ² ) и т. д. Большинство объектов или форм имеют края и углы. Длина и ширина этих ребер учитываются при расчете площади конкретной формы.

Как рассчитать площадь?

Давайте посмотрим, как вычислить площадь фигуры с помощью сетки. Площадь любой фигуры — это количество единичных квадратов, которые могут в нее поместиться. Сетка состоит из множества квадратов со сторонами 1 на 1 единицу. Площадь каждого из этих квадратов равна 1 квадратной единице. Следовательно, каждый квадрат известен как единичный квадрат. Посмотрите на рисунок, показанный ниже. Найдем площадь фигуры, начерченной на сетке.

Площадь этой фигуры равна количеству заштрихованных единичных квадратов.

Таким образом, площадь фигуры = 9 квадратных единиц. Теперь давайте посмотрим на другой пример.

Когда фигура не занимает полного единичного квадрата, мы можем аппроксимировать и найти ее значение. Если он занимает примерно 1/2 единичного квадрата, мы можем объединить две такие половины, чтобы образовать площадь в 1 квадратную единицу. Обратите внимание на приведенный ниже рисунок.

Здесь площадь, занимаемая фигурой, равна 4 полным квадратам и 8 полуквадратам. Вместе это образует площадь 8 квадратных единиц. Если заштрихованная область меньше 1/2, мы можем опустить эти части. Для правильных фигур у нас есть определенные формулы для вычисления их площади. Обратите внимание, что это только приблизительное значение.

Площадь прямоугольника

Площадь прямоугольника — это площадь, занимаемая им. Рассмотрим желтый прямоугольник в сетке. Он занял 6 единиц.

В приведенном выше примере длина прямоугольника составляет 3 единицы, а ширина — 2 единицы. Площадь прямоугольника получается путем умножения его длины и ширины, что равносильно подсчету единиц квадратов. Таким образом, формула площади прямоугольника: : Площадь прямоугольника = длина × ширина. В данном случае это будет 2 × 3 = 6 квадратных единиц.

Площадь квадрата

Площадь квадрата – это занимаемая им площадь. Посмотрите на цветной квадрат, показанный в сетке ниже. Он занимает 25 квадратов.

Из рисунка видно, что длина каждой стороны цветного квадрата равна 5 единицам. Следовательно, площадь квадрата – это произведение его сторон, которое можно представить по формуле: Площадь квадрата = сторона × сторона. Итак, площадь этого квадрата = 5 × 5 = 25 квадратных единиц.

Площадь круга

Круг представляет собой изогнутую форму. Площадь круга – это количество пространства, заключенного в границах круга. Узнайте больше о π и радиусе, прежде чем мы перейдем к формуле площади круга.

Площадь круга рассчитывается по формуле: π r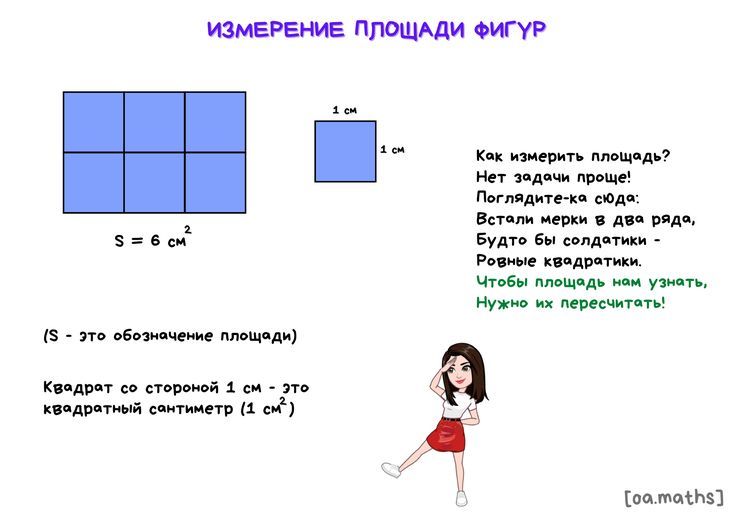

2 , где π – математическая константа, значение которой округляется до 3,14 или 22/7 и r — это радиус окружности.

Площадь геометрических фигур — Формула

Каждая форма имеет разные размеры и формулы. В следующей таблице показан список формул для площади различных форм.

Форма	Площадь фигур — Формула
Квадрат	Площадь квадрата = x 2 квадратных единиц
Прямоугольник	Площадь прямоугольника = длина × ширина = l × w квадратных единиц
Круг	Площадь круга = π r 2 квадратных единиц
Треугольник	Площадь треугольника = \(\dfrac{1}{2}\times b \times h\) квадратных единиц
Параллелограмм	Площадь параллелограмма = основание × высота = b × h квадратных единиц
Равнобедренная трапеция	Площадь равнобедренной трапеции = \(\dfrac{1}{2}(a+b) h\) квадратных единиц
Ромб	Площадь ромба = \(\dfrac{1}{2}\times (d1) \times (d2)\) квадратных единиц
Воздушный змей	Площадь воздушного змея = \(\dfrac{1}{2}\times (d1) \times (d2)\) квадратных единиц

☛ Связанные темы по площади

Ознакомьтесь со следующими темами, касающимися областей различной формы, и узнайте больше о формулах площади.

• Формула геометрической площади
• Площадь треугольника

Советы и подсказки

• Мы часто запоминаем формулы для вычисления площади фигур. Более простым методом было бы использование линий сетки, чтобы понять, как была получена формула.
• Мы часто путаем площадь и периметр фигуры. Полное понимание может быть построено путем отслеживания поверхности любой формы и наблюдения за тем, что область — это, по сути, пространство или область, покрытая формой.

 

Примеры на участке

1. Пример 1: Найдите площадь квадрата со стороной 7 см.

   Решение :

   Площадь квадрата = сторона × сторона. Здесь сторона = 7 см

   Подставляя значения, 7 × 7 = 49.

   Следовательно, площадь квадрата = 49 квадратных см.

2. Пример 2: Размеры прямоугольника 15 см и 8 см. Найдите его площадь.

   Решение :

   Площадь прямоугольника равна произведению его длины на ширину, что можно представить по формуле: Площадь = l × w.
   Подставляя данные значения, получаем площадь прямоугольника = 15 × 8 = 120 см ²

3. Пример 3: Можете ли вы найти площадь круга с радиусом 14 см?

   Раствор :

   Радиус круга = 14 см

   Площадь круга рассчитывается по формуле π r ²

   Подставляя значения в формулу, площадь = \(\dfrac{22}{7}\) × 14 × 14 = 616 квадратных см.

4. Пример 4. Вычислите площадь заданной формы путем подсчета квадратов.

    

   Решение: Давайте посчитаем полные квадраты и половинки квадратов.

   Есть 24 единичных квадрата и 5 полуквадратов.
   Следовательно, площадь фигуры = 24 + (5 × ½) = 24 + 2,5 26,5 квадратных единиц

перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду

Как ваш ребенок может освоить математические понятия?

Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу Cuemath.

Записаться на бесплатный пробный урок

Практические вопросы по области

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по Зоне

Что такое площадь?

Площадь фигуры представляет собой двумерную величину, которая измеряется в квадратных единицах, таких как квадратные дюймы или (в ² ), квадратные футы или (футы ² ), квадратные ярды или (ярды ² ), и т.д.

Как найти площадь неправильной формы?

Площадь неправильной формы можно найти, разделив фигуру на единичные квадраты. Когда фигура не занимает весь единичный квадрат, мы можем аппроксимировать и найти ее значение.

Как доказать площадь круга?

Если окружность сложить в треугольник, радиус станет высотой треугольника, а периметр станет его основанием, равным 2 × π × r. Мы знаем, что площадь треугольника находится путем умножения его основания и высоты, а затем деления на 2, что составляет: ½ × 2 × π × r × r. Следовательно, площадь круга равна π r ² .

Что такое периметр и площадь треугольника?

Общая длина границы замкнутой формы называется ее периметром. Другими словами, периметр — это сумма сторон двумерной фигуры. Периметр треугольника равен сумме трех сторон треугольника, а площадь треугольника равна

Какие формулы площади и периметра квадрата и прямоугольника?

Формулы площади и периметра квадрата и прямоугольника следующие. Площадь квадрата = сторона × сторона. Периметр квадрата = 4 × сторона. Площадь прямоугольника = длина × ширина. Периметр прямоугольника = 2 × (длина + ширина)

Почему площадь выражается в квадратных единицах?

Площадь фигуры — это количество единичных квадратов, необходимое для ее полного покрытия. Поэтому он измеряется и выражается в квадратных единицах.

Единицы СИ – Площадь | НИСТ

Кредит: Pixabay, Вид с воздуха на сельхозугодья

Площадь — это площадь поверхности, которую может покрыть двумерная фигура, измеряемая в квадратных единицах.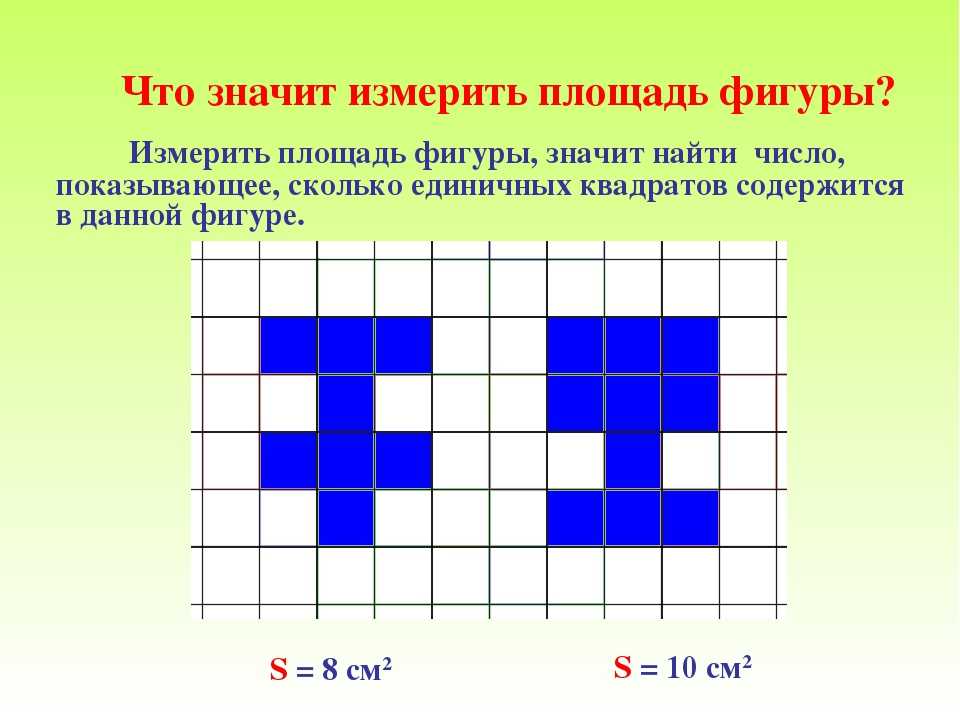 Единицей площади в СИ является квадратный метр (м ² ), который является производной единицей.

Общие единицы площади
100 квадратных миллиметров (мм 2 )	= 1 квадратный сантиметр (см 2 )
100 см 2	= 1 квадратный дециметр (дм 2 )
100 дм 2	= 1 квадратный метр (м 2 )
100 м 2	= 1 квадратный декаметр (плотина 2 ) = 1 ар
100 дамба 2	= 1 квадратный гектометр (hm 2 ) = 1 гектар (га)
100 мм 2	= 1 квадратный километр ( км 2 )

Кредит: Почтовая служба США, марка с флагом США навсегда (2019 г. ))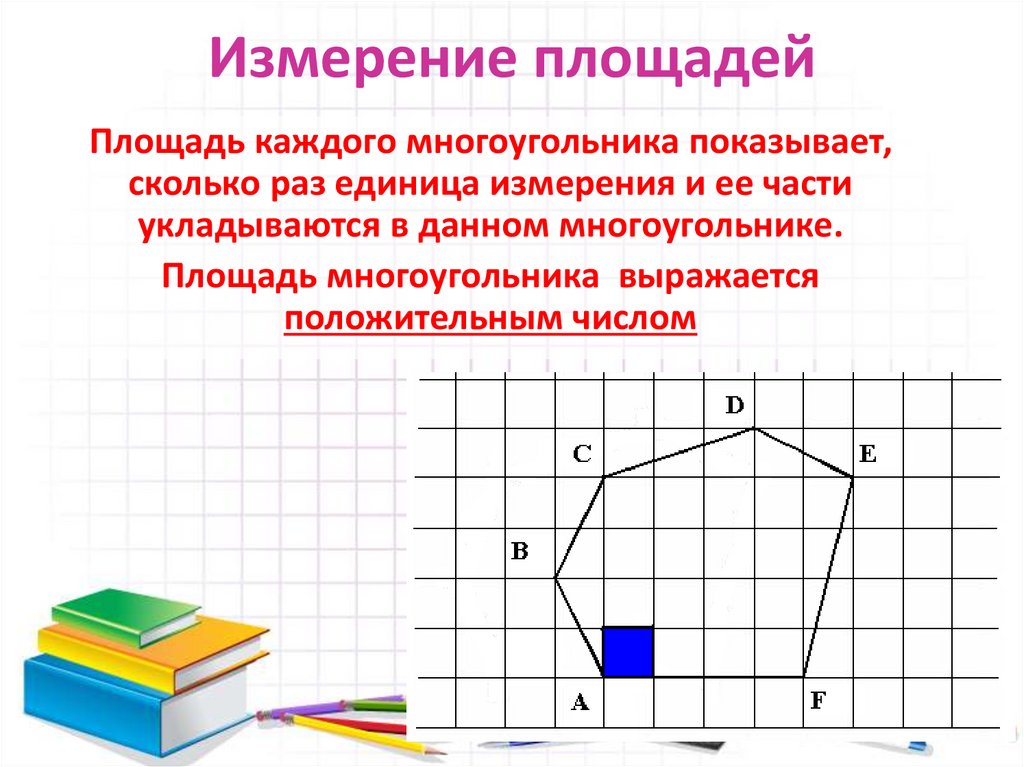

• Квадратный миллиметр (мм ² ) можно представить в виде квадрата со стороной 1 мм (или 1 мм x 1 мм).
• Квадратный сантиметр (см ² ) можно представить как квадрат со стороной 1 см (или 1 см х 1 см).
• Квадратный метр (м ² ) можно представить как квадрат со стороной 1 м (или 1 м x 1 м). Квадратные метры используются в промежуточных целях, например, для расчета площади комнаты для покупки нужного количества ковра.
• гектар — это специальное название для 10 000 квадратных метров (м ² ), которые можно представить в виде квадрата со стороной 100 м (или 100 м x 100 м). Большие площади в черте города или размер фермы могут измеряться в гектарах (га).
Квадратный километр
• (км ² ) можно представить в виде квадрата со стороной 1 км (или 1 км х 1 км). Квадратные километры обычно измеряют очень большие площади.

 

Повседневные зоны
550 мм 2 (25 мм x 22 мм)	Почтовая марка США первого класса
616 см 2 (22 см x 28 см)	Офисная бумага
1,8 м 2 (2 м x 0,9 м)	Наружная дверь жилого помещения
162 м 2 (9 м x 18 м)	Волейбольная площадка NCAA
7,77 га (0,0777 км 2 )	Ландшафт Мемориального парка Джефферсона, Вашингтон, округ Колумбия
7 га (0,07 км 2 )	Мемориальный парк Линдона Бейнса Джонсона, Вашингтон, округ Колумбия

Ресурсы:

• Метрический расчет количества осадков и интенсивность осадков (Геологическая служба США).
  Как измеряется площадь: Ошибка 403 — доступ запрещён