Как посчитать квадраты: Как посчитать квадратуру комнаты, стен, потолка, пола

Как посчитать квадратуру комнаты, стен, потолка, пола

Временами требуется узнать площадь или объем комнаты, чтобы произвести расчеты на приобретение различных материалов для строительства или ремонта помещения. В процессе ремонта приходится измерять площадь стен, чтобы определиться с количеством обоев или других отделочных материалов. Как правило, расчеты начинаются с замеров. Замеры осуществляются с помощью рулетки или другими способами.

Содержание

• 1 Как посчитать площадь комнаты?
• 2 Прямоугольные помещения
• 3 Комната неправильной формы
• 4 Как подсчитать площадь стен
• 5 Как определить объем комнаты
• 6 Заключение

Как посчитать площадь комнаты?

Это не сложный процесс, поскольку существуют определенные формулы. В данном случае, достаточно определиться с размерами. Для этого необходимо:

• приобрести рулетку, самую обычную, желательно на 5 метров;
• взять бумагу, карандаш или ручку;
• иметь калькулятор, хотя не сложно посчитать и на бумаге.

С помощью этого, минимального набора приспособлений и осуществляются все необходимые расчеты. Лучше конечно, иметь помощника, но, в крайнем случае, можно все делать самому. Габариты комнаты измеряются вдоль стен, если они не заставлены мебелью. Если нужны точные размеры, то лучше мебель отставить и освободить стены. Лишь после этого рекомендуется производить все измерения. При этом, следует учитывать тот фактор, что правильных комнат, с прямыми углами практически не существует, если дело касается помещений, сооруженных еще в советские времена. В связи с этим, необходимо весьма серьезно отнестись к процессу измерения.

Прямоугольные помещения

Если комната имеет правильную (относительно) прямоугольную форму, без всевозможных выступов или ниш, то площадь ее вычисляется довольно просто. Для начала, нужно измерить длину и ширину комнаты, после чего результаты записать на бумажке, чтобы не забыть. Измерения можно производить как в метрах, так и в сантиметрах. Если замеры осуществляются в метрах, то после целых значений метров ставится запятая, а потом пишутся сантиметры. Например, 4 метра, 35 сантиметров следует записать: 4,35 м.

Измерив длину, например, 2,35 м и ширину 1,4 м, данные перемножаются. Например: 2,35 м х 1,4 м. В результате получается 3,290 м2 или 3,29 м². Как правило, после запятой всегда оставляется две цифры. Если их больше, то значение округляется по правилам, которые излагались еще в начальных классах школы. При этом, можно округлять или до метров, или до сантиметров, в зависимости от требуемой точности. В основном, достаточно измерять с точностью до метров и лишь изредка требуется точность до сантиметров.

Комната неправильной формы

Не все комнаты имеют правильную форму. Довольно часто встречаются помещения с наличиями выступов различной формы. В таких случаях, помещения делятся на отдельные квадраты, прямоугольники или треугольники, в зависимости от конфигурации выступов. Затем измеряются все выступы, после чего рассчитывают их площадь и все полученные результаты суммируют.

На фото выше представлен пример, где в комнате имеется выступ прямоугольной формы.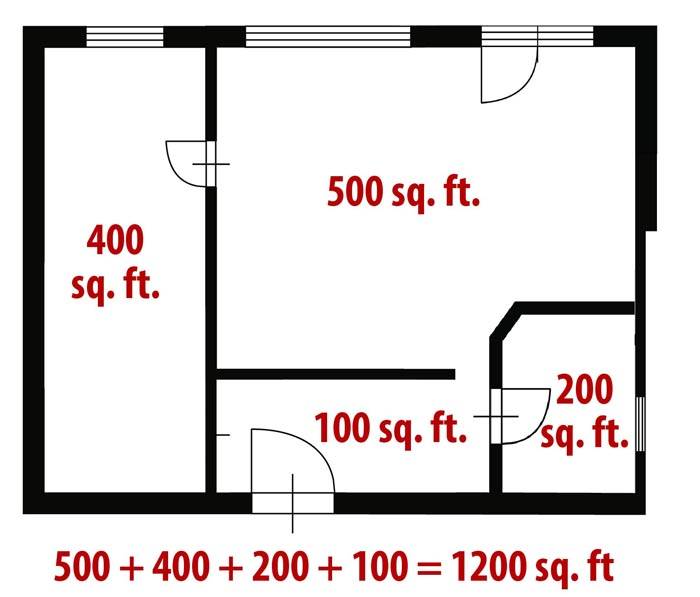 В таком случае, площадь комнаты вычисляется следующим образом:

1. Подсчитывается общая площадь без выступа: 3,6м х 8,5м = 30,6м².
2. Вычисляется площадь выступа: 3,25м х 0,8м = 2,6м².
3. Полученные результаты складываются: 30,6м² + 2,6м² = 33,2м².

Встречаются комнаты со скошенными стенами. Поступают следующим образом: стена разбивается так, что получается прямоугольник и треугольник (см. рисунок ниже). В результате для расчетов, необходимо иметь пять размеров. Впоследствии, вычисляют отдельно площади фигур, а потом все результаты либо складывают, либо вычитаются, в зависимости от характера выступа.

Квадратуру обсчитывают в таком порядке:

1. Подсчитывается основная прямоугольная часть: 6,5 м х 1,4 м = 8,96м². Округляя получаем 9,0 м².
2. Вычисляется площадь малого прямоугольника: 2,7м х 1,9м = 5,13м². При округлении получаем 5,0 м².
3. Подсчитывается площадь треугольника, имеющего прямой угол (1,3м х 1,9м) / 2 = 1,235м². Округлив получится 1 м².
4. В заключение, полученные результаты складываются: 9+5+1 = 15 м².

Подобная точность вычислений абсолютно приемлема. Как правило, планировка помещений бывает разнообразной, но правило подсчетов абсолютно одинаковы: все делится на отдельные, независимые фигуры, подсчитывается площадь отдельных фигур, а потом все складывается, а может и вычитается, в зависимости от конфигурации выступов. Особенно это актуально при определении площади пола или потолка.

Как подсчитать площадь стен

Квадратуру стен необходимо знать, когда планируется закупка отделочных материалов, таких как обои, шпаклевка, краска и другие. Если это глухая стена, то здесь все просто – измеряется высота и длина стены, после чего результаты перемножаются. Если в стене расположен оконный или дверной проем, то нужно определить, какую площадь они занимают и отнять от общей площади стены. Поэтому:

• измеряют высоту стен и их ширину;
• узнают высоту и ширину дверных проемов;
• измеряют высоту и ширину оконных проемов.

Глухая стена

• 2,5 м х 6,0м = 15 м² – площадь глухой стены.

Стена с дверным проемом:

1. Общая площадь стены: 2,5м х 6,0м = 15м².
2. Площадь дверного проема: 2,1м х 1,0м = 2,1м².
3. Площадь стены без дверей: 15м² – 2,1м² = 12,9м².

Стена с оконным проемом:

• Общая площадь стены: 2,5м х 4м = 10м².
• Площадь оконного проема: 1,3м х 1,5м = 1,95м².
• Площадь стены без окна: 10 м² – 1,95 м² = 8,05м².

Как правило, вычисляют общую площадь всех стен. Для этого берут и складывают полученные результаты площадей каждой стены. Например: 15м² + 12,9м² + 10м² + 8,05м² = 45,95м².

Как определить объем комнаты

Иногда, для некоторых расчетов необходимо знать, какой объем занимает комната. Для подобных расчетов нужно знать еще одну цифру: не только длину и ширину, но и высоту комнаты. В результате расчетов получается кубатура (объем) комнаты, которая обозначается в метрах кубических. Например:

• длина помещения – 6 м;
• ширина помещения – 4 м;
• высота помещения – 2,5 м.

Теперь нужно все показатели перемножить: 6м х 4м х 2,5м = 60м³. Итак, получается, что объем помещения составляет 60 м³.

Заключение

Подобная точность расчетов на конечный результат особо не влияет, поскольку мало кто приобретает облицовочные материалы исходя из подобных расчетов. Как правило, приобретают любые облицовочные материалы с некоторым запасом. Если, например, считают количество керамической плитки, то расчеты производят по количеству штук, исходя из схемы укладки. Даже в этом случае, ее берут с некоторым избытком. Это связано еще и с тем, что возможны нештатные ситуации, связанные с порчей облицовочного материала. Особенно это актуально, когда работы выполняются самостоятельно, без привлечения профессионалов.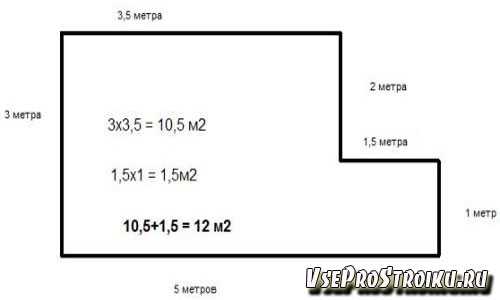

Это относится и к таким материалам, как обои, линолеум, ламинат, различная вагонка, сайдинг и т.д. Нужно всегда помнить, что при работах появляются отходы и, причем, их может быть немало, если размеры произвольные, без учета применения тех или иных материалов.

Подобный подход особенно актуален при укладке линолеума, который имеет стандартные размеры по ширине. Что касается его длины, то тут нужно очень точно все измерить и всегда сантиметров 10, но добавить. Если просчитаться, то это может дорого обойтись.

Математика 4 класс. 11 октября. Площадь и метр квадратный

Watch this video on YouTube

Как посчитать площадь комнаты, стены, пола, потолка

Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты.  О том, как посчитать площадь комнаты и стен, объем помещения и пойдет речь дальше.  

Часто требуется посчитать кубатуру комнаты, ее объем

Содержание статьи

• 1 Площадь комнаты в квадратных метрах
  • 1.1 Прямоугольная комната
  • 1.2 Помещение неправильной формы
• 2 Как рассчитать квадратуру стен
• 3 Объем комнаты

Площадь комнаты в квадратных метрах

Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:

• Рулетка. Лучше — с фиксатором, но подойдет и обычная.
• Бумага и карандаш или ручка.
• Калькулятор (или считайте в столбик или в уме).

Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.

Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине.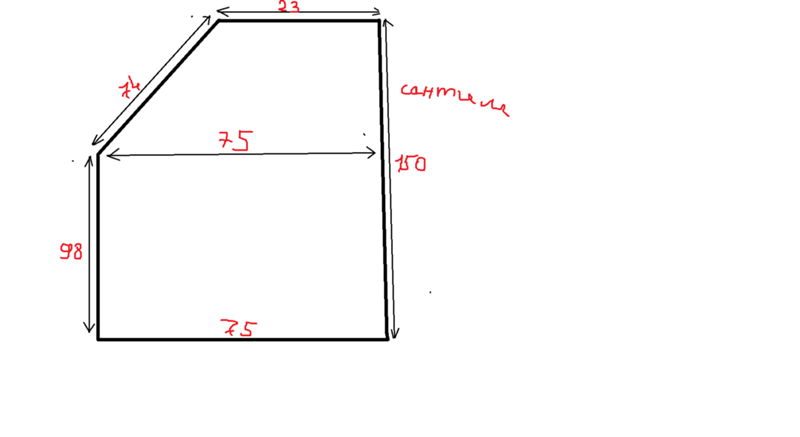 Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.

Прямоугольная комната

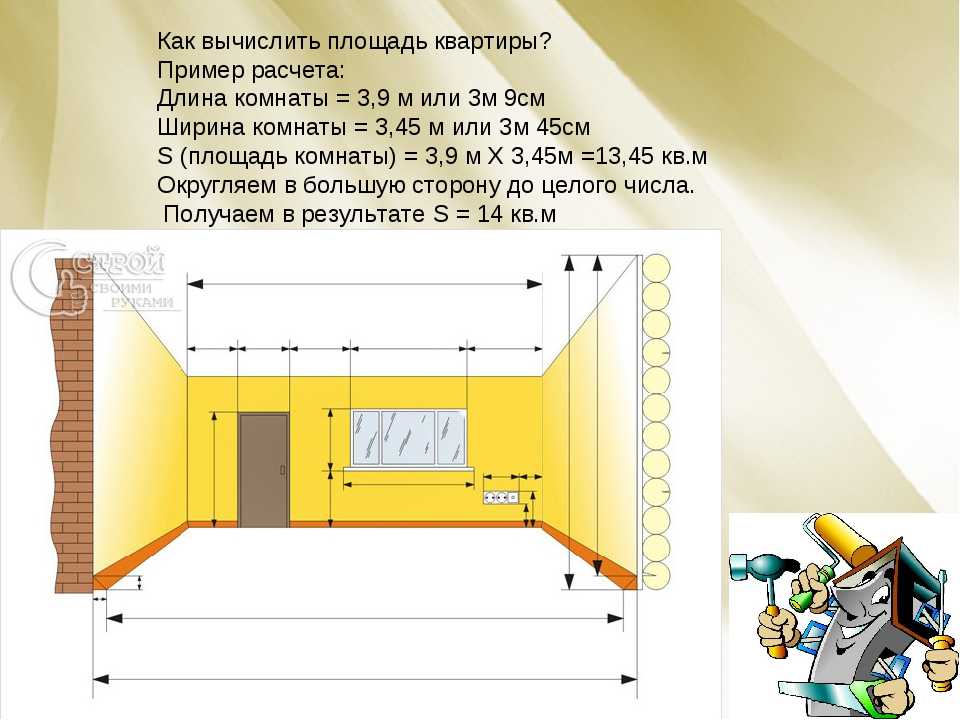
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).

Как высчитать площадь комнаты

Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м.  В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.

Помещение неправильной формы

Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).

Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.

Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.

Площадь комнаты сложной формы

Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):

1. Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
2. Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
3. Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.

Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту.

Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.

Как посчитать площадь комнаты неправильной формы

В этом случае порядок вычислений такой:

1. Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
2. Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
3. Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
4. Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.

Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.

Формулы расчета площади и периметра простых геометрических фигур

Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.

Как рассчитать квадратуру стен

Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:

• высота потолков;
• высота и ширина дверных проемов;
• высота и ширина оконных проемов.

Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.

Удобнее всего размеры наносить на план

Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.

1. Стена с дверью:
   • 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
   • сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв. м.
   • стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
2. Стена с окном:
   1. квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
   2. сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,85 кв.м.
   3. стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.

Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.

Объем комнаты

Формула расчета объема комнаты

Для некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:

• длинна — 5,6 м;
• ширина — 3,2 м;
• высота — 2,5 м.

Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м³. Итак, объем помещения 44,8 куба.

 

Сколько квадратов и прямоугольников на этой картинке

В этой статье обсуждались формулы для нахождения

числа квадратов и прямоугольников в данной фигуре из ‘ n’ количество строк и ‘m’ число столбцов

Содержание

• 1 Подсчет количества квадратов и прямоугольников в заданной сетке N x M | Как считать квадрат в рассуждениях
  • 1.1 Сколько квадратов в данной фигуре
  • 1.2 Сколько прямоугольников на данной фигуре

 Подсчитать количество квадратов и количество прямоугольников в заданной сетке N x M | Как считать квадраты в рассуждениях

Сколько квадратов в данной фигуре

Сколько квадратов в фигуре одинакового количества строк и столбцов

(т.е. количество квадратов в квадратной сетке)

Пример – 1 :

  Сколько квадратов в сетке 4 x 4

Решение : На приведенном выше рисунке 4 строки и 4 столбца.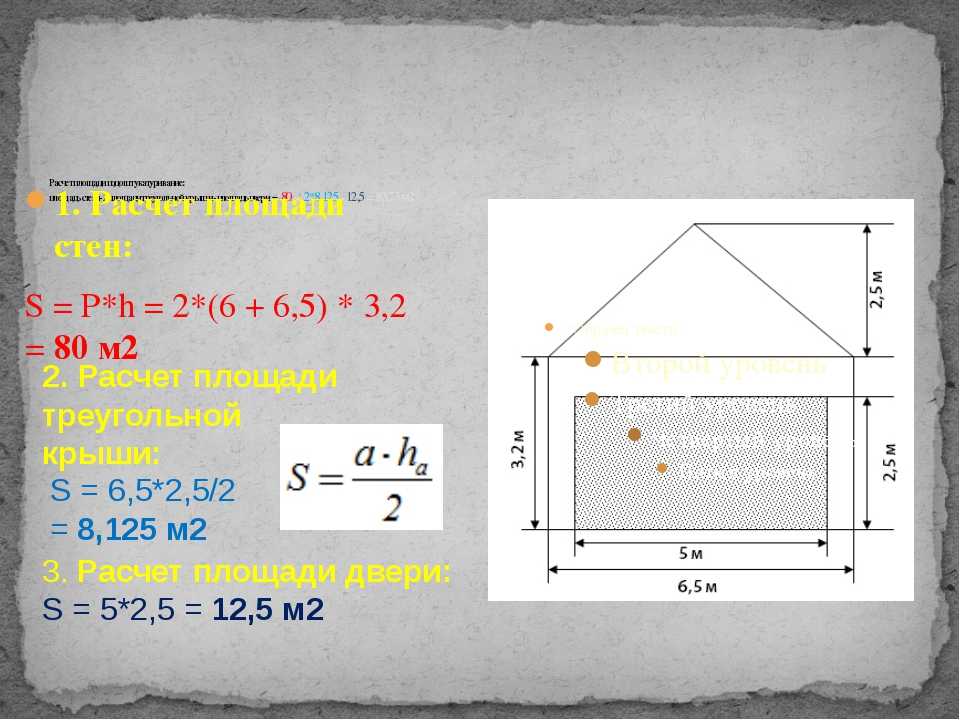 Итак, пусть n = 4

. Здесь мы используем два типа формул для нахождения количества квадратов в сетке n x n следующим образом:

-2) ² + – – – – – + (n – n) ²

Теперь подставим n = 4 в вышеприведенную формулу

= 4 ² + ( 4-1) ²   + (4- 2 ) ² + (4 – 3) ²   + (4 – 4) ²

= 16 + 9 + 4 + 1 + 0 = 30

Формула – 2

900 = 4 в приведенной выше формуле

= 4 x 5 x 9 / 6 = 30

Таким образом, количество квадратов в сетке 4 x 4 равно 30

Пример -2
Сколько квадратов в сетке 5 x 5

Решение . На приведенном выше рисунке 5 строк и 5 столбцов. Следовательно, n=5

Формула

n ² + (n -1 ) ² + (n — 2) ² + – – – – – + (n – n)
2 Итак по 0 выше заменить n = 5

= 5 ² + ( 5-1) ² + (5- 2 ) ² + (5 – 3) ² + (5 – 4) ² + ( 5 – 5) ²

= 25 + 16 + 9 + 4 + 1 + 0 = 55

Количество квадратов в сетке 5 х 5 равно 55

Сколько квадратов на рисунке n ‘ количество строк и ‘m’ количество столбцов

(то есть количество квадратов в прямоугольной сетке)

Пример – 3 Сколько квадратов в сетке 3 x 4

Решение : На приведенном выше рисунке 4 строки и 5 столбцов.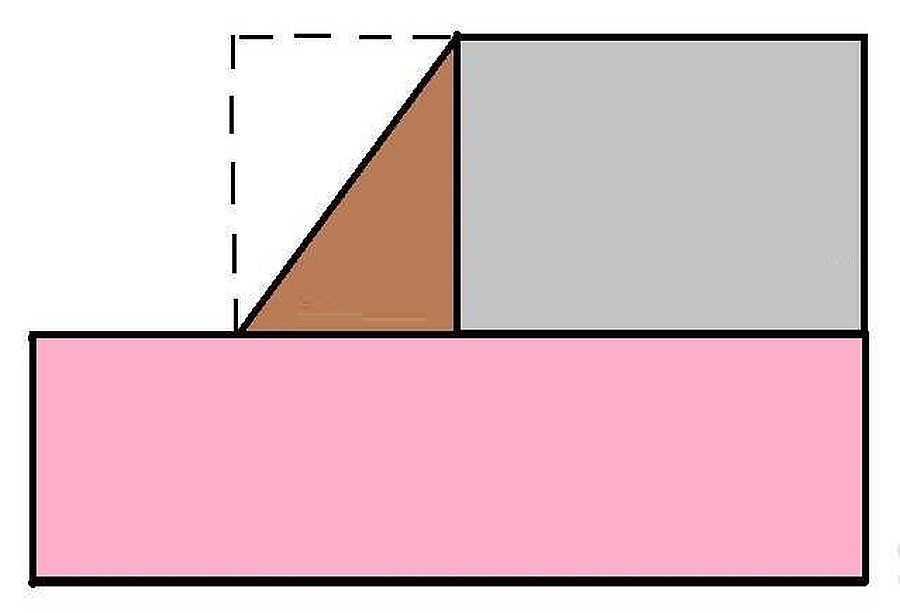

Пусть количество строк (n)= 4 и количество столбцов (m) = 5

Здесь мы используем следующие простые формулы

Формула- 1 1)  + (n-2) ( m- 2)  + – – – – – + (n – n ) или (m – m)

Теперь подставьте n = 5 и m = 4

= (4 x 5) + (4 – 1) (5 – 1) + (4 – 2) (5 – 2) + (4 – 3) (5 – 3) + (4 – 4) (5 – 4)

= 20 + 12 + 6 + 2 +0 = 40

Формула- 2

n = 5 и m = 4. Теперь подставьте эти значения в формулы выше в данной цифре = 40

Сколько прямоугольников на данной фигуре

Подсчитать количество прямоугольников на фигуре с одинаковым количеством строк и столбцов сетки

(т.е. Подсчет прямоугольников внутри квадрата)

– Пример Сколько прямоугольников в сетке 5 x 5

Решение . На приведенном выше рисунке 5 строк и 5 столбцов.

Пусть количество строк или столбцов ( n)=5

Здесь для нахождения прямоугольников есть два метода

Формула – 1

[n + ( n -1 ) + ( n -2 ) + ( n -3 ) + – – – – –  + ( n -n )] ²

Теперь замените значения’ n ‘в приведенной выше формуле

= [ 5 + (5 – 1 ) + (5 – 2 ) + (5 – 3 ) + (5 – 4 ) + (5 – 5) ] ²

= [ 5 + 4 + 3+ 2 + 1 +0 ] ²

= 15 x 15 = 2250009

Теперь подставьте значения n в приведенную выше формулу = 225

Общее количество прямоугольников на данном рисунке = 225

Подсчет количества прямоугольников на рисунке ‘n’ количество строк и ‘m’ количество столбцов

(т.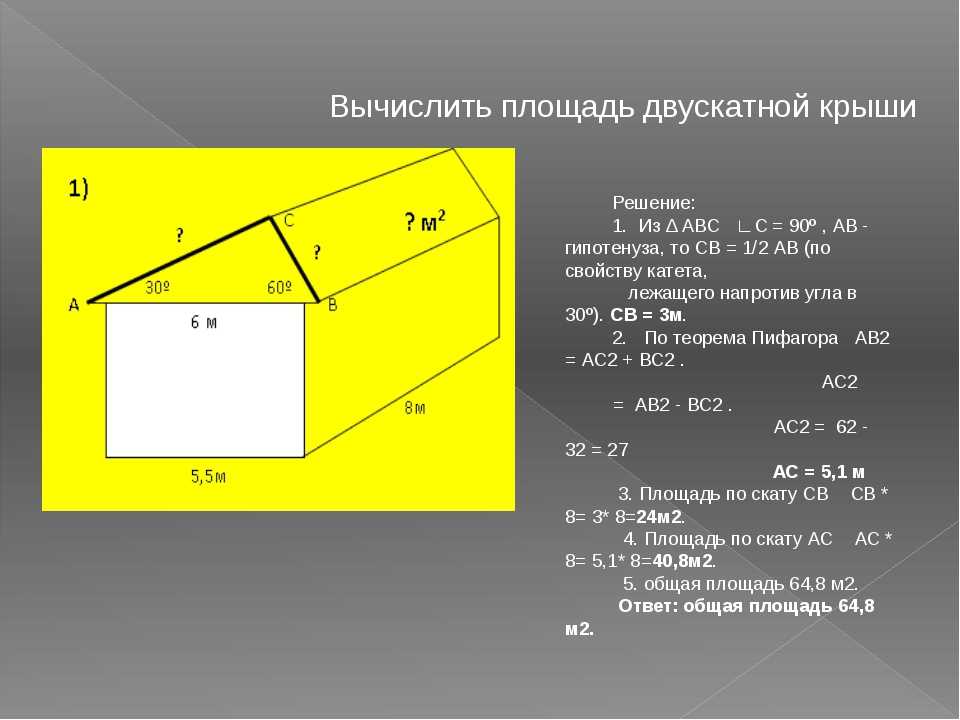 е. подсчетов внутри прямоугольников прямоугольник )

Пример – 5  Сколько прямоугольников в сетке 4 x 5

Решение: На приведенном выше рисунке 4 строки и 5 столбцов.

Пусть количество строк ( n)=4 и количество столбцов (m) = 5

Здесь для нахождения прямоугольников есть два метода

Формула – 1 ( Формула для нахождения количества прямоугольников в фигуре ‘n ‘ количество строк и ‘m’ — количество столбцов)

[n + ( n -1 ) + ( n -2 ) + ( n -3 ) + – – – – –  + ( n -n )] x [м + (м -1 ) + (м -2 ) + (м -3 ) + – – – – – + (м -м )]

Теперь подставьте значения « n » и « m » в приведенную выше формулу

= [ 4 + (4 – 1 ) + (4 – 2 ) + (4 – 3 ) + (4 – 4) )] x [ ​​5 + (5 – 1 ) + (5 – 2 ) + (5 – 3 ) + (5 – 4 ) + (5 – 5) ]

= [ 4 +3 +2 +1 +0 ] x [ 5 + 4 + 3+ 2 + 1 +0 ]

= 10  x 15 = 150

Формула – 2   

 

Теперь подставьте значения ‘ n 3 ‘0

0 и приведенная выше формула

= 4 х 5 х 5 х 6 / 4 = 150

Общее количество прямоугольников на данном рисунке =  150

Статьи по теме

Подсчитайте количество треугольников | Найдите количество треугольников на данной фигуре Как найти цифру единицы степени числа

Система счисления » вики полезно Как легко найти общее количество множителей для больших чисел

Основные понятия системы счисления в математике

Комбинаторика — Подсчет количества латинских квадратов

Спросил 6 лет, 5 месяцев назад

Изменено 6 лет, 5 месяцев назад

Просмотрено 4k раз

$\begingroup$

Подсчет количества латинских квадратов — сложная задача. Я понимаю, что обычно используется формула $n!(n-1)!$ (число или уменьшенные латинские квадраты). Как видно здесь и на многих других страницах, вы можете погуглить.

Но мне интересно, может ли кто-нибудь объяснить, как это работает? Есть ли формула или метод для расчета количества сокращенных латинских квадратов? Также как появляются числа $n!(n-1)!$? Это потому, что в первой строке и первом столбце может быть так много различных комбинаций чисел?

• комбинаторика
• латинский квадрат

$\endgroup$

3

$\begingroup$

Если $L_n$ — количество латинских квадратов порядка $n$, а $R_n$ — количество приведенных латинских квадратов порядка $n$, то $$L_n = n!(n-1)! R_n.$$ Фактор $n! (n-1)!$ получается путем подсчета:

• Для любого латинского квадрата порядка $n$ существует уникальных перестановок столбцов, так что первая строка находится в порядке ($1,2,\ ldots,n$), после чего идет

  уникальная перестановка строк, которая фиксирует первую строку так, чтобы первый столбец был в порядке.

• В обратном направлении, если задан редуцированный латинский квадрат порядка $n$, если мы переставим строки, кроме первой, и переставим столбцы, мы получим $n! (n-1)!$ различных латинских квадратов порядка $n$.

Итак, каждому сокращенному латинскому квадрату соответствует $n! (n-1)!$ (не обязательно редуцированные) латинские квадраты, и каждый (не обязательно редуцированный) латинский квадрат дает ровно один редуцированный латинский квадрат.

Таким образом, вычисление $L_n$ фактически совпадает с вычислением $R_n$. Хотя существует множество формул для вычисления числа латинских квадратов, в вычислительном отношении они эффективны только до $n=11$. При использовании наилучшей в настоящее время методики подсчета (метод Сада) по мере совершенствования аппаратного обеспечения мы можем увидеть $L_{12}$ в течение нашей жизни.

• Насколько я знаю, метод Сада — единственный метод, который применялся для $n \geq 10$.

• Для заказов $n \leq 9$ можно генерировать представителей основного класса для каждого основного класса, вычисляя размер их основного класса с помощью nauty, сумма которых равна $L_n$ (непростая задача для $n=9$ [Я не уверен, что кто-то действительно делал это таким образом]; представителей можно загрузить с веб-сайта Брендана Маккея за $n \leq 8$).

  Как посчитать квадраты: Как посчитать квадратуру комнаты, стен, потолка, пола