Как посчитать площадь если все стороны разные: Как найти площадь фигуры, формула

Онлайн калькулятор: Площадь многоугольника

УчебаМатематикаГеометрия

Расчет площади многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники

Пример многоугольника

Данный калькулятор обсчитывает площадь многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники.

Смотрим на картинку — площадь многоугольника ABCDE можно вычислить как сумму площадей треугольников ABD, BCD и ADE. Для этого, понятно, помимо длин сторон многоугольника, надо знать еще и длины диагоналей BD и AD, но это и все что нужно — площадь любого треугольника можно вычислить только по длинам его сторон, без измерения углов.

А это довольно удобно, например, при бытовом ремонте — длины-то всяко проще померять, чем углы.

Итак, измеряем длины сторон интересующего нас многоугольника, заносим их в таблицу, мысленно разбиваем многоугольник на треугольники, измеряем нужные диагонали, также заносим их в таблицу, после чего калькулятор рассчитывает площадь всей фигуры. Для проверки также выводятся площади обсчитанных им треугольников. В поле «Ошибка» выводится вершина, которую не удалось сопоставить ни одному треугольнику (если, например, введены еще не все диагонали).

По умолчанию в таблицу введены стороны и диагонали многоугольника на картинке, что легко исправить, нажав кнопку «Очистить таблицу».

Площадь многоугольника

Стороны и диагонали

	Название стороны или диагонали	Длина

Записей:

51020501001000

Стороны и диагонали

Название стороны или диагонали

Импортировать данныеОшибка импорта

Данные

Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: ? EFGHIJKLMNOPQRSTUVWXYZ ?;50.5

Загрузить данные из csv файла

Точность вычисления

Знаков после запятой: 2

Площадь

 

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.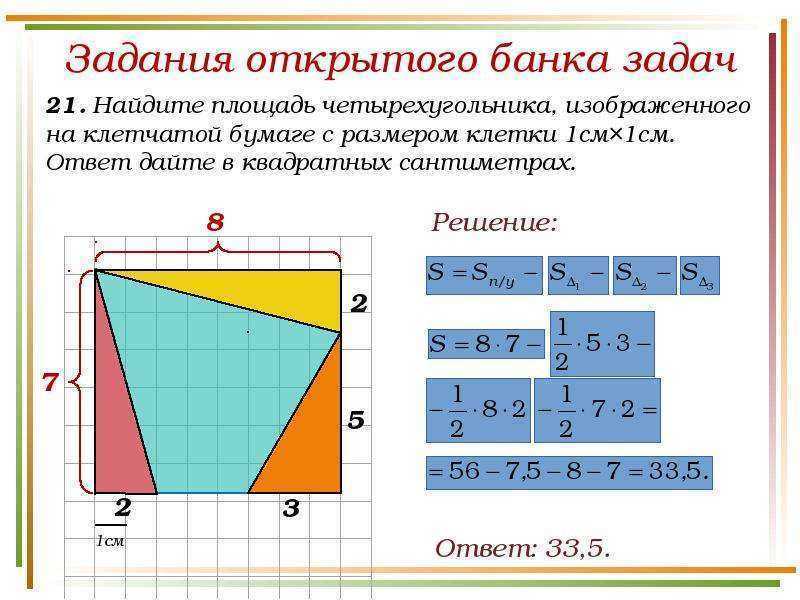

Ошибка

 

Ссылка скопирована в буфер обмена

Похожие калькуляторы

• • Расчет площади треугольника по формуле Герона
• • Площадь треугольника по координатам вершин
• • Площадь правильного многоугольника
• • Длина стороны правильного многоугольника
• • Вычисление площади выпуклого многоугольника по координатам вершин на плоскости
• • Раздел: Геометрия ( 94 калькуляторов )

 Геометрия Математика многоугольник площадь треугольник формула Герона

 PLANETCALC, Площадь многоугольника

Timur2020-11-03 14:19:28

Площадь четырехугольника

Главная

 → 

Геометрия

 → 

Площадь четырехугольника

Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн. Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных.

Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.

В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.

Таблица с формулами площади четырехугольника (в конце страницы)

— Вычисления   (показано)   (скрыто)

— примечания   (показано)   (скрыто)

1

Площадь четырехугольника по диагоналям и углу между ними

… подготовка …

d₁ — диагональ

d₂ — диагональ

α° — угол между диагоналями

---

2

Площадь четырехугольника через стороны и углы между этими сторонами

При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:

. .. подготовка …

a — сторона

b — сторона

c — сторона

d — сторона

α° — угол между сторонами

β° — угол между сторонами

---

3

Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты

Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.

При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:

… подготовка …

a — сторона

b — сторона

c — сторона

d — сторона

---

4

Площадь четырехугольника в который можно вписать окружность

Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.

При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:

… подготовка …

a — сторона

b — сторона

c — сторона

d — сторона

r — радиус вписанной окружности

---

5

Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними

Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.

… подготовка …

a — сторона

b — сторона

c — сторона

d — сторона

α° — угол между сторонами

β° — угол между сторонами

---

Примечание:

Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°

---

Таблица с формулами площади четырехугольника

	исходные данные (активная ссылка для перехода к калькулятору)	эскиз	формула
1	диагональ и угол между ними
2	стороны и углы между этими сторонами		где  ,
3	стороны (по Формуле Брахмагупты)		где
4	стороны и радиус вписанной окружности		где
5	стороны и углы между ними

---

Площадь частных случаев четырехугольников

Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:

• площадь квадрата
• площадь трапеции
• площадь параллелограмма
• площадь прямоугольника
• площадь ромба

---

Определения

Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.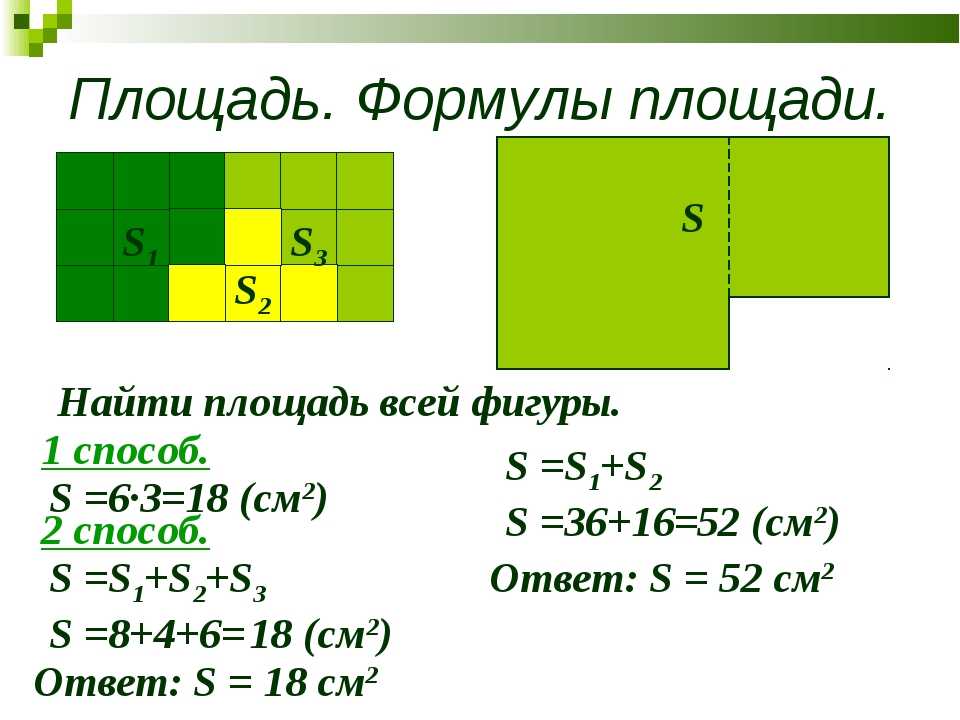

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Площадь четырехугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.

Площадь измеряется в единицах измерения в квадрате: км², м², см², мм² и т.д.

Калькулятор площади

. Найдите площадь 16 популярных фигур!

Создано Ханной Памула, кандидатом наук

Отредактировано Bogna Szyk и Jack Bowater

Последнее обновление: 20 октября 2022 г.

Содержание:

• Что такое площадь в математике? Определение площади
• Как рассчитать площадь?
• Формула площади квадрата
• Формула площади прямоугольника
• Формула площади треугольника
• Формула площади круга
• Формула площади сектора
• Формула площади эллипса
• Формула площади трапеции
• Формула площади параллелограмма
• Формула площади ромба
• Формула площади воздушного змея
• Формула площади пятиугольника
• Формула площади шестиугольника
Формула площади 90 и восьмиугольника формула кольца
• Формула площади четырехугольника
• Формула площади правильного многоугольника
• Часто задаваемые вопросы

Если вам интересно, как рассчитать площадь любой базовой фигуры, вы находитесь в правильном месте — этот калькулятор площади ответит на все ваши вопросы. Используйте наш интуитивно понятный инструмент, чтобы выбрать одну из шестнадцати различных фигур и вычислить их площадь в мгновение ока. Ищете ли вы определение площади или, например, площадь формулы ромба, мы обеспечим вас. Продолжайте прокручивать, чтобы узнать больше, или просто поиграйте с нашим инструментом — вы не будете разочарованы!

Что такое площадь в математике? Определение площади

Проще говоря, площадь — это размер поверхности . Другими словами, его можно определить как пространство, занимаемое плоской формой. Чтобы понять концепцию, обычно полезно представить площадь как количество краски, необходимое для покрытия поверхности . Посмотрите на рисунок ниже – все фигуры имеют одинаковую площадь, 12 квадратных единиц:

Существует множество полезных формул для вычисления площади простых фигур. В разделах ниже вы найдете не только известные формулы для треугольников, прямоугольников и окружностей, но и другие формы, такие как параллелограммы, воздушные змеи или кольца.

Мы надеемся, что после этого объяснения у вас не возникнет проблем с определением области математики!

Как рассчитать площадь?

Ну конечно, это зависит от формы ! Ниже вы найдете формулы для всех шестнадцати фигур, представленных в нашем калькуляторе площади. Для ясности мы перечислим только уравнения — их изображения, пояснения и выводы можно найти в отдельных абзацах ниже (а также в инструментах, посвященных каждой конкретной фигуре).

Вы готовы? Вот самые важные и полезные формулы площади для шестнадцати геометрических фигур:

• Квадрат формула площади: A = a²
• Прямоугольник Формула площади: A = a × b
• Формулы площади треугольника :
  • А = b × h / 2 или
  • A = 0,5 × a × b × sin(γ) или
  • A = 0,25 × √( (a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c)) или
  • A = a² × sin(β) × sin(γ) / (2 × sin(β + γ))
• Круг формула площади:
  A = πr²
• Сектор круга Формула площади: A = r² × угол / 2
• Эллипс формула площади: A = a × b × π
• Трапеция Формула площади: A = (a + b) × h / 2
• Формулы площади параллелограмма :
  • А = а × ч или
  • A = a × b × sin(угол) или
  • A = e × f × sin(угол)
• Ромб Формулы площади:
  • А = а × ч или
  • А = (е × f) / 2 или
  • A = s² × sin(угол)
• Кайт формулы площади:
  • А = (е × f) / 2 или
  • А = а × b × sin(γ)
• Формула площади Пентагона : A = a² × √(25 + 10√5) / 4
• Шестиугольник
  Формула площади: A = 3/2 × √3 × a²
• Октагон формула площади: A = 2 × (1 + √2) × a²
• Формула площади кольца : A = π(R² - r²)
• Четырехугольник формула площади: A = e × f × sin(угол)
• Правильный многоугольник Формула площади: A = n × a² × cot(π/n) / 4

Хотите изменить единицу площади? Просто нажмите на название устройства, и появится раскрывающийся список.

Формула площади квадрата

Вы забыли, что такое формула площади квадрата? Тогда вы находитесь в правильном месте. Площадь квадрата равна произведению длины его сторон:

• Площадь квадрата = a × a = a² , где a — сторона квадрата

Это самая основная и наиболее часто используемая формула, хотя существуют и другие. Например, есть формулы площади квадрата, в которых используются диагональ, периметр, радиус описанной окружности или внутренний радиус.

Формула площади прямоугольника

Формула площади прямоугольника тоже несложна — это просто произведение сторон прямоугольника:

• Площадь прямоугольника = a × b

Расчет площади прямоугольника чрезвычайно полезен в повседневных ситуациях: от строительства здания (оценка необходимой плитки, настила, сайдинга или определения площади крыши) до отделки вашей квартиры (сколько мне нужно краски или обоев?) до расчета, сколько люди, которых ваш торт может накормить.

Формула площади треугольника

Существует много различных формул для площади треугольника, в зависимости от того, что дано и какие законы или теоремы используются. В этом калькуляторе площади мы реализовали четыре из них:

1. Даны основание и высота

• Площадь треугольника = b × h / 2

2. Даны две стороны и угол между ними (SAS)

• Площадь треугольника = 0,5 × a × b × sin(γ)

3. Даны три стороны (SSS) (Эта формула площади треугольника называется Формула Герона )

• Площадь треугольника = 0,25 × √( (a + b + c) × (-a + b + в) × (а - б + в) × (а + б - в))

Вы можете узнать больше в калькуляторе формул Герона.

4. Даны два угла и сторона между ними (ASA)

• Площадь треугольника = a² × sin(β) × sin(γ) / (2 × sin(β + γ))

Существует особый тип треугольника, прямоугольный треугольник.

В этом случае основание и высота — это две стороны, образующие прямой угол. Тогда площадь прямоугольного треугольника может быть выражена как:

Площадь прямоугольного треугольника = a × b / 2

Формула площади круга

Формула площади круга является одной из самых известных формул:

• Площадь круга = πr² , где r — радиус круга

В этом калькуляторе мы реализовали только это уравнение, но в нашем калькуляторе круга вы можете рассчитать площадь по двум разным формулам:

1. Диаметр

• Площадь круга = πr² = π × (d / 2)²

2. Окружность

• Площадь круга = c² / 4π

Кроме того, формула площади круга удобна в повседневной жизни – например, при решении серьезной дилеммы, какой размер пиццы выбрать.

Формула площади сектора

Формулу площади сектора можно найти, взяв пропорцию окружности. Площадь сектора пропорциональна его углу, поэтому, зная формулу площади круга, мы можем написать, что:

α / 360° = площадь сектора / площадь круга

Преобразование угла говорит нам, что 360° = 2π

α / 2π = Площадь сектора / πr²

Итак:

• Площадь сектора = r² × α / 2

Формула площади эллипса

Чтобы найти формулу площади эллипса, сначала вспомните формулу площади круга: πr² . Для эллипса у вас есть не одно значение радиуса, а два разных значения: a и b . Единственная разница между формулами площади круга и эллипса заключается в замене r² произведением большой и малой полуосей, a × b :

• Площадь эллипса = π × a × b

Формула площади трапеции

Площадь трапеции можно найти по следующей формуле:

• Площадь трапеции = (a + b) × h / 2 , где a и
  74 длины параллельных сторон и высота

  Кроме того, формула площади трапеции может быть выражена как:

  Площадь трапеции = m × h , где м — среднее арифметическое длин двух параллельных сторон

  Площадь параллелограмма формула

  Хотите ли вы вычислить площадь, зная основание и высоту, стороны и угол, или диагонали параллелограмма и угол между ними, вы находитесь в правильном месте. В нашем инструменте вы найдете три формулы площади параллелограмма:

  1. Основание и высота

  • Площадь параллелограмма = a × h

  2. Стороны и угол между ними

  • Площадь параллелограмма = a × b × sin(α)

  3. Диагонали и угол между ними

  • Площадь параллелограмма = e × f × sin(θ)

  Формула площади ромба

  Мы реализовали три полезные формулы для вычисления площади ромба. Вы можете найти площадь, если знаете:

  1. Сторона и высота

  • Площадь ромба = a × h

  2. Диагонали

  • Площадь ромба = (e × f) / 2

  3. Сторона и любой угол, например, α

  • Площадь ромба = a² × sin(α)

  Формула площади воздушного змея

  Для расчета площади воздушного змея можно использовать два уравнения, в зависимости от того, что известно:

  1. Формула площади воздушного змея с учетом диагоналей воздушного змея

  • Площадь воздушного змея = (e × f) / 2

  2. Площадь воздушного змея по формуле с двумя неконгруэнтными сторонами и углом между этими двумя сторонами

  • Площадь воздушного змея = a × b × sin(α)

  Формула площади пятиугольника

  Площадь пятиугольника можно рассчитать по формуле:

  • Площадь пятиугольника = a² × √(25 + 10√5) / 4 , где - сторона 9007 правильный пятиугольник

  Воспользуйтесь нашим специальным калькулятором пятиугольника, где представлены другие основные свойства правильного пятиугольника: сторона, диагональ, высота и периметр, а также радиус описанной и вписанной окружности.

  Формула площади шестиугольника

  Основная формула площади шестиугольника:

  • Площадь шестиугольника = 3/2 × √3 × a² , где a — сторона правильного шестиугольника

  Итак, откуда берется формула? Вы можете думать о правильном шестиугольнике как о наборе шести конгруэнтных равносторонних треугольников. Чтобы найти площадь шестиугольника, нам нужно найти площадь одного треугольника и умножить ее на шесть. Формула площади правильного треугольника равна квадрату стороны, умноженному на квадратный корень из 3, деленному на 4:

  Площадь равностороннего треугольника = (a² × √3) / 4

  Площадь шестиугольника = 6 × Площадь равностороннего треугольника = 6 × (a² × √3) / 4 = 3/2 × √3 × a²

  Формула площади восьмиугольника

  Чтобы найти площадь восьмиугольника, все, что вам нужно сделать, это знать длину стороны и следующую формулу:

  • Площадь восьмиугольника = 2 × (1 + √2) * a²

  Площадь восьмиугольника также может быть рассчитана по формуле:

  Площадь восьмиугольника = периметр × апофема / 2

  Периметр в восьмиугольном случае — это просто 8 × a . А что такое апофема? Апофема — это расстояние от центра многоугольника до середины стороны. В то же время это высота треугольника, полученного путем проведения линии из вершин восьмиугольника в его центр. Этот треугольник — один из восьми конгруэнтных — является равнобедренным, поэтому его высота может быть рассчитана, например, с помощью теоремы Пифагора по формуле:

  h = (1 + √2) × a / 4

  Итак, наконец, мы получаем первое уравнение:

  Площадь восьмиугольника = периметр * апофема / 2 = (8 × a × (1 + √2) × a / 4) / 2 = 2 × (1 + √2 ) × a²

  Площадь кольца формула

  Кольцо представляет собой кольцеобразный объект – область, ограниченную двумя концентрическими окружностями разного радиуса. Найти площадь по формуле кольца несложно, если вы помните формулу площади круга. Только взгляните: площадь кольца — это разность площадей большего круга радиуса R и меньшего круга радиуса r:

  • Площадь кольца = πR² - πr² = π(R² - r²)

  Формула площади четырехугольника

  Формула четырехугольника, которую реализует этот калькулятор площади, использует две заданные диагонали и угол между ними.

  • Площадь четырехугольника = e × f × sin(α) , где e и f — диагонали.

  Мы можем использовать любой из двух углов при вычислении их синуса. Зная, что два смежных угла дополнительные, можно утверждать, что sin(угол) = sin(180° - угол) .

  Если вы ищете другие формулы площади четырехугольника, воспользуйтесь нашим специальным калькулятором четырехугольника, где вы найдете формулу Бретшнайдера (для четырех сторон и двух противоположных углов) и формулу, в которой используются бимедианы и угол между ними. их.

  Формула площади правильного многоугольника

  Формула площади правильного многоугольника выглядит следующим образом:

  • Площадь правильного многоугольника = n × a² × cot(π/n) / 4

  , где n — количество сторон, а — длина стороны.

  Существуют и другие уравнения, в которых используются, например, такие параметры, как радиус описанной окружности или периметр. Вы можете найти эти формулы в специальном параграфе нашего калькулятора площади многоугольника.

  Если вы имеете дело с неправильным многоугольником, помните, что вы всегда можете разделить фигуру на более простые фигуры, например, на треугольники. Просто посчитайте площадь каждого из них и, в конце, просуммируйте их. Разложение многоугольника на множество треугольников называется триангуляцией многоугольника.

  Часто задаваемые вопросы

  Какой четырехугольник имеет наибольшую площадь?

  Для заданного периметра четырехугольник с максимальной площадью всегда будет квадратом .

  Какая фигура имеет наибольшую площадь при заданном периметре?

  Для заданного периметра замкнутая фигура максимальной площади представляет собой круг .

  Как рассчитать площадь неправильной формы?

  Чтобы вычислить площадь неправильной формы:

  1. Разделите фигуру на несколько подформ, для которых можно легко вычислить площадь, например треугольники, прямоугольники, трапеции, (полу)круги и т. д.
  2. Вычислите площадь каждой из этих подформ.
  3. Суммируйте площади подформ, чтобы получить окончательный результат.

  Как рассчитать площадь под кривой?

  Чтобы найти площадь под кривой на интервале, необходимо вычислить определенный интеграл функции, описывающей эту кривую, между двумя точками, соответствующими концам рассматриваемого интервала.

  Ханна Памула, кандидат наук

  Площадь круга

  Посмотрите 23 похожих калькулятора 2D-геометрии 📏

  Площадь прямоугольникаПлощадь полумесяцаЦентр масс… Еще 20

  Как найти площадь неправильной формы? Определение, примеры, факты

  Площадь неправильных форм

  Неправильные формы представляют собой многоугольники с пятью или более сторонами различной длины. Эти формы или фигуры можно разложить на треугольники, квадраты и четырехугольники для оценки площади.

  Некоторые примеры неправильной формы:

  Предметы повседневной жизни неправильной формы

  Вычисление площади неправильной формы:

  Подходы к оценке площади неправильной формы:

  Оценка площади с использованием единичных квадратов и неправильные четырехугольники. В этом методе разделите фигуру на единичные квадраты. Общее количество единичных квадратов, попадающих в фигуру, определяет общую площадь.

  Рисунок: Некоторые примеры неправильной формы

  Считайте квадрат как «1», если заштрихованная область покрывает более половины при расчете площади для более точной оценки.

  Рисунок: Для неправильной формы подсчитайте квадраты с оранжевым и желтым кодом как 1.

  На следующем рисунке подсчитайте площадь, подсчитав единичные квадраты, что равно 6. Если мы обозначим каждую единицу квадрата в сантиметрах , площадь будет 6 см2.

  Рисунок: Расчет площади неправильной формы с изогнутыми краями

  • Разделение неправильной формы на две или более правильных фигур

  Используйте этот метод для неправильных форм, которые представляют собой комбинацию треугольников и многоугольников. Используйте предопределенные формулы для расчета площади таких фигур и сложите их вместе, чтобы получить общую площадь.

  Например, неправильную форму мы делим несколькими ребрами на треугольник и три многоугольника.

  Общая площадь фигуры определяется как:

  ⇒ Площадь = Площадь (ABIM) + Площадь (BCGH) + Площадь (CDEF) + Площадь (JKL)

  ⇒ Площадь = (AB × BI) + (BC × CG) + (CD × DE) + ( 1 ⁄ 2 × LJ × KO)

  ⇒ Площадь = ( 10 × 5) + (3 × 3) + (2 × 2) + ( 1 ⁄ 2 × 4 × 4) 

  ⇒ Площадь = 50 + 9 + 4 + 8

  ⇒ Площадь = 71 см2

  900 с делением неправильной формы кривые двух или более правильных форм

  В этом методе неправильная форма разбивается на несколько квадратов, треугольников или других четырехугольников. В зависимости от формы и изгибов часть фигуры может быть также кругом, полукругом или квадрантом.

  Следующая фигура представляет собой неправильную форму с 8 сторонами, включая одну кривую. Определить неизвестные величины по заданным размерам сторон. Разложите фигуру на два прямоугольника и полукруг.

  Площадь фигуры ABCDEF равна:

  Площадь (ABCDEF) = Площадь (ABCG) + Площадь (GDEF) + Площадь (aob)

  Площадь = (AB × AG) + (GD × DE) + ( 1 ⁄ 2 × π × ob 2 )

  Площадь = (3 × 4) + (10 × 4) + ( 1 ⁄ 2 × 3,14 × 1 2 )

  Площадь = 12 + 40 + 1,57

  Площадь = 53,57 см архитектура и разметка сельскохозяйственных полей. Мы применяем концепцию в раскрое тканей согласно заданному дизайну. В старших классах эта техника закладывает основу для более сложных тем, таких как вычисление объема, рисование конических сечений и фигур эллиптической формы.

  Забавный факт . Многоугольники Танграма являются древними примерами геометрических фигур и могут создавать более 6500 форм.

  • квадрат
  • Прямоугольник
  • Треугольник
  • Круг
  • Область
  • Нерегулярные и регулярные формы

  Практические задачи

  29 квадратных единиц

  9000 210000 29000 29000 29000 29000 29000 29000 29000 29000 29000 29000 29000 29000 29000 29000 29000 29000 29000 29000 29000 29000 29000 2 29000 29000 29000 29000 2 29000 29000 29000 2 29000 2 29000 2 29000 2 29000 2 29000 2 29000 2 29000 29000 2 29000 29000 29000 29000 29000 29000 2 29000 29000 29000 29000 2 29000 29000 2 22 29.

  Правильный ответ: 22 квадратных единицы
  : Полностью закрытые клетки считаются как есть. Каждая более чем наполовину закрытая клетка считается за 1 клетку. Менее чем наполовину закрытые квадраты считаются как 0 каждый.
  Таким образом, у нас есть 10 $ + (1 × 12) + (0 × 14) = 10 + 12 = 22 $ квадратных единиц.

  48 кв. см

  24 кв. см

  70 кв. см

  10 кв. см

  Правильный ответ: 70 кв. см
  Площадь прямоугольника 1 = 5 × 6 = 30 кв.см.
  Площадь прямоугольника 2 = 8 × 5 = 40 кв. см
  Площадь поля = площадь прямоугольника 1 + площадь прямоугольника 2
  = 30 + 40 = 70 кв.см.

  Умножить

  Сложить

  Вычесть

  Разделить

  Правильный ответ: Сложить
  Чтобы найти площадь неправильной формы, мы сначала разбиваем фигуру на обычные фигуры. Затем мы находим площадь каждой фигуры и складываем их. Например, если неправильный многоугольник состоит из квадрата и треугольника, то: Площадь неправильного многоугольника = Площадь квадрата + Площадь треугольника.

  25 кв. см

  34 кв. см

  9 кв. см

  16 кв. см

  Правильный ответ: 34 кв. см
  Площадь квадрата 1 = 5 × 5 = 25 кв. см.
  Площадь квадрата 2 = 3 × 3 = 9 кв. см.
  Площадь неправильного многоугольника = площадь квадрата 1 + площадь квадрата 2 = 25 + 9 = 34 квадратных см.

  Часто задаваемые вопросы

  Как найти площадь неправильной формы?

  Неправильная форма может быть разложена на известные многоугольники. Тогда площадь неправильной формы равна сумме площадей каждого из этих многоугольников. Если неправильная форма имеет изогнутые края и невозможно разложить всю форму на известные многоугольники, то лучшим подходом будет оценка площади.

  I s Есть ли какая-нибудь формула для нахождения областей неправильной формы?

  Нет, общей формулы для расчета площади неправильной формы не существует, потому что стороны могут быть разной длины и кривизны.

  Где нам нужно найти площадь неправильной формы в реальной жизни?

  Нам нужно найти площадь неправильной формы для рисования карт, построения архитектуры и обозначения сельскохозяйственных полей.

  Как посчитать площадь если все стороны разные: Как найти площадь фигуры, формула