Как посчитать площадь если все стороны разные: Как узнать площадь четырех угольника если все четыре стороны разные?

7 способов найти площадь прямоугольника

10 марта 2020 Ликбез Образование

Выбирайте формулу, ориентируясь на известные величины.

1. Если известны две соседние стороны

Просто перемножьте две стороны прямоугольника.

• S — искомая площадь прямоугольника;
• a и b — соседние стороны.

2. Если известны любая сторона и диагональ

Найдите квадраты диагонали и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте длину известной стороны на полученное число.

• S — искомая площадь прямоугольника;
• a — известная сторона;
• d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).

3. Если известны любая сторона и диаметр описанной окружности

Найдите квадраты диаметра и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте известную сторону на полученное число.

• S — искомая площадь прямоугольника;
• a — известная сторона;
• D — диаметр описанной окружности.

4. Если известны любая сторона и радиус описанной окружности

Найдите квадрат радиуса и умножьте результат на 4.

Отнимите от полученного числа квадрат известной стороны.

Найдите корень из результата и умножьте на него длину известной стороны.

• S — искомая площадь прямоугольника;
• a — известная сторона;
• R — радиус описанной окружности.

5. Если известны любая сторона и периметр

Умножьте периметр на длину известной стороны.

Найдите квадрат известной стороны и умножьте полученное число на 2.

От первого произведения отнимите второе и разделите результат на 2.

• S — искомая площадь прямоугольника;
• a — известная сторона;
• P — периметр прямоугольника (равен сумме всех сторон).

6. Если известны диагональ и угол между диагоналями

Найдите квадрат диагонали.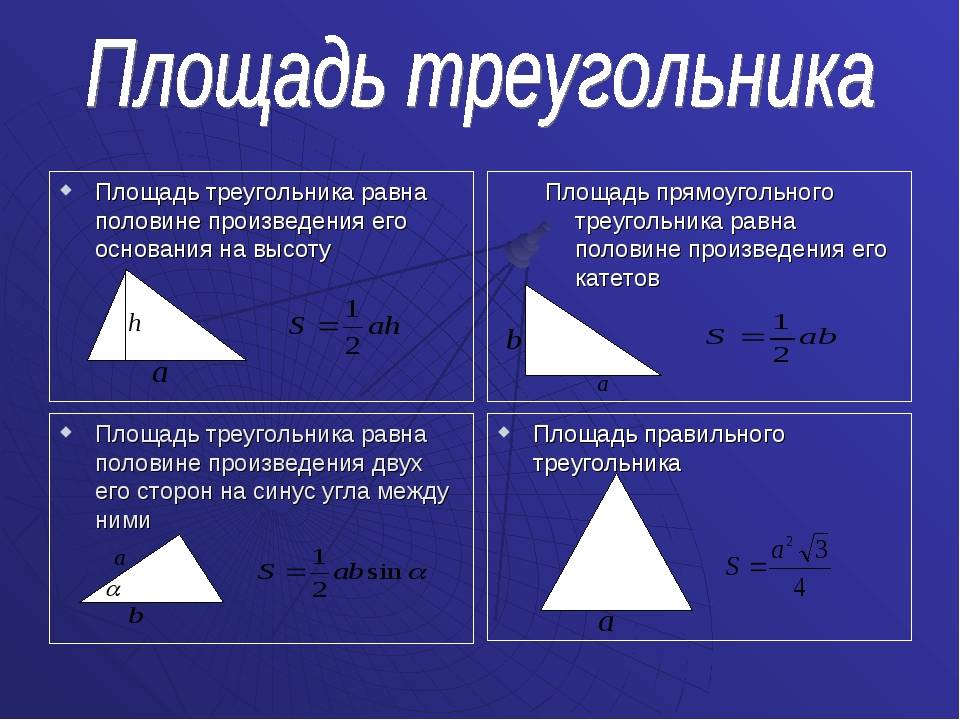

Разделите полученное число на 2.

Умножьте результат на синус угла между диагоналями.

• S — искомая площадь прямоугольника;
• d — любая диагональ прямоугольника;
• α — любой угол между диагоналями прямоугольника.

7. Если известны радиус описанной окружности и угол между диагоналями

Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.

Умножьте полученное число на 2, а потом на синус угла между диагоналями.

• S — искомая площадь прямоугольника;
• R — радиус описанной окружности;
• α — любой угол между диагоналями прямоугольника.

Читайте также 🎓❓📐

• ТЕСТ:​ ​​Умеете ли вы считать в уме?
• Как легко и быстро считать проценты в уме
• Как найти площадь любого треугольника
• ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
• Как освоить устный счёт школьникам и взрослым

Онлайн калькулятор: Площадь многоугольника

УчебаМатематикаГеометрия

Расчет площади многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники

Пример многоугольника

Данный калькулятор обсчитывает площадь многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники.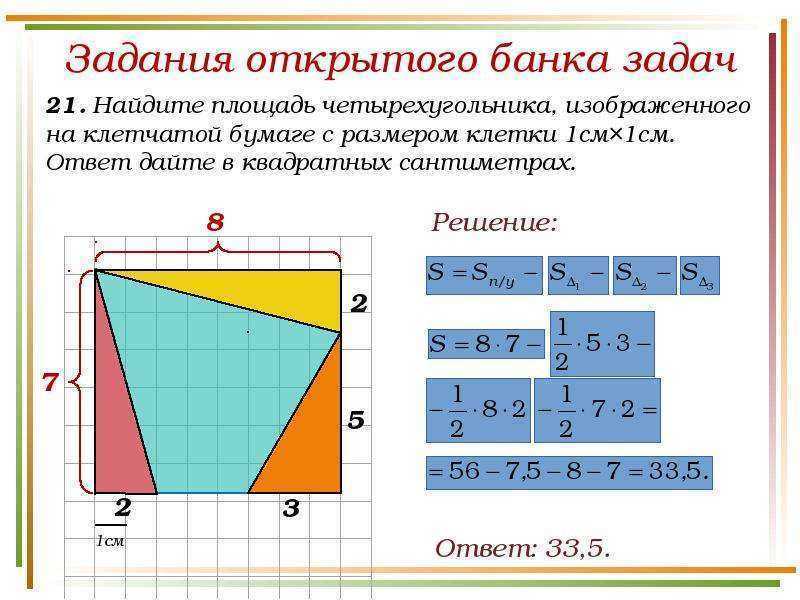

Смотрим на картинку — площадь многоугольника ABCDE можно вычислить как сумму площадей треугольников ABD, BCD и ADE. Для этого, понятно, помимо длин сторон многоугольника, надо знать еще и длины диагоналей BD и AD, но это и все что нужно — площадь любого треугольника можно вычислить только по длинам его сторон, без измерения углов.

А это довольно удобно, например, при бытовом ремонте — длины-то всяко проще померять, чем углы.

Итак, измеряем длины сторон интересующего нас многоугольника, заносим их в таблицу, мысленно разбиваем многоугольник на треугольники, измеряем нужные диагонали, также заносим их в таблицу, после чего калькулятор рассчитывает площадь всей фигуры. Для проверки также выводятся площади обсчитанных им треугольников. В поле «Ошибка» выводится вершина, которую не удалось сопоставить ни одному треугольнику (если, например, введены еще не все диагонали).

По умолчанию в таблицу введены стороны и диагонали многоугольника на картинке, что легко исправить, нажав кнопку «Очистить таблицу».

Площадь многоугольника

Стороны и диагонали

	Название стороны или диагонали	Длина

Записей:

51020501001000

Стороны и диагонали

Название стороны или диагонали

Импортировать данныеОшибка импорта

Данные

Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: ? EFGHIJKLMNOPQRSTUVWXYZ ?;50.5

Загрузить данные из csv файла

Точность вычисления

Знаков после запятой: 2

Площадь

 

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Ошибка

 

Ссылка скопирована в буфер обмена

Похожие калькуляторы

• • Расчет площади треугольника по формуле Герона
• • Площадь треугольника по координатам вершин
• • Площадь правильного многоугольника
• • Длина стороны правильного многоугольника
• • Вычисление площади выпуклого многоугольника по координатам вершин на плоскости
• • Раздел: Геометрия ( 96 калькуляторов )

 Геометрия Математика многоугольник площадь треугольник формула Герона

 PLANETCALC, Площадь многоугольника

Timur2020-11-03 14:19:28

Научитесь измерять площадь неправильных фигур

Ключевые понятия

• Как разбить большую площадь на меньшие
• Разделить неправильную фигуру на квадраты и прямоугольники
• Найти площадь каждого отдельного квадрата и прямоугольника
• Найти площадь площадь любой неправильной формы

1.

1 Площадь квадрата

1. В квадрате все стороны имеют одинаковую длину.
2. Площадь квадрата = Сторона x Сторона
3. Сторона = 6 дюймов
4. Площадь = 6 дюймов x 6 дюймов = 36 квадратных дюймов

1,2 Площадь прямоугольника

Так как площадь противоположных сторон у прямоугольника одинакова

Площадь прямоугольника = Длина * Ширина

Длина = 8 дюймов, ширина = 5 дюймов

Площадь = 8 дюймов x 5 дюймов = 40 квадратных дюймов

Джек хочет постелить на земле искусственную траву для игры в гольф. Давайте поможем Джеку найти площадь земли, которая будет покрыта травой.

Метод 1

Начертите фигуру на бумаге с сеткой и посчитайте количество закрытых квадратов, чтобы найти площадь.

Общее количество квадратов = 56

Площадь покрытия травой = 56 квадратных футов

Метод 2

• Разбейте большую площадь на более мелкие части.
• Ищите возможности, в которых меньшие фигуры являются частью большей формы.
• Разделите большую площадь на меньшие прямоугольники и найдите площадь.

Покрытие поля для гольфа разделено на прямоугольники A, B и C

Поиск отдельных участков

Площадь прямоугольника A = 4 фута x 3 фута = 12 квадратных футов

Площадь прямоугольника B = 4 фута x 3 фута = 12 квадратных футов

Площадь прямоугольника C = 4 фута x 8 футов = 32 квадратных фута

Общая площадь = 12 + 12 + 32 = 56 квадратных футов

 Шаги для нахождения площади неправильной формы

1. Найдите все неизвестные стороны.
2. Разделить неправильную форму на квадраты и прямоугольники
3. Найдите площадь каждого отдельного квадрата и прямоугольника
4. Сложите все отдельные площади, чтобы найти общую площадь неправильной формы.
   Общая площадь = сумма всех отдельных площадей

  Шаги по нахождению площади неправильной формы

1. Найдите все неизвестные стороны.

В этом примере найдите значения стороны a и стороны b

Сторона a = 10 – 3 = 7 см

Сторона b = 5 – 3 = 2 см

2. Разделите неправильную форму на квадраты и прямоугольники

В примере фигура разделена на один прямоугольник-A и один квадрат-B

Общая площадь = площадь прямоугольника A + площадь квадрата B

Шаги для нахождения площади неправильной формы

3. Найти площадь каждого отдельного квадрата и прямоугольника

Площадь прямоугольника A = длина x ширина

= 10 x 2 = 20 квадратных см

Площадь квадрата B = сторона x сторона

= 3 x 3 = 9 квадратных см

4. Сложите все отдельные площади, чтобы найти общую площадь неправильной формы 9.0031

Общая площадь = площадь прямоугольника A + площадь прямоугольника B

= 20 кв. см + 9 кв. см

= 29 кв. см

Пример: найти площадь заштрихованной части

Общая площадь заштрихованная часть = площадь внешнего прямоугольника – площадь внутреннего прямоугольника

площадь внешнего прямоугольника = 10 см x 8 см

= 80 квадратных см

площадь внутреннего прямоугольника = 4 см x 6 см

= 24 квадратных см

Общая площадь заштрихованной части = 80 кв.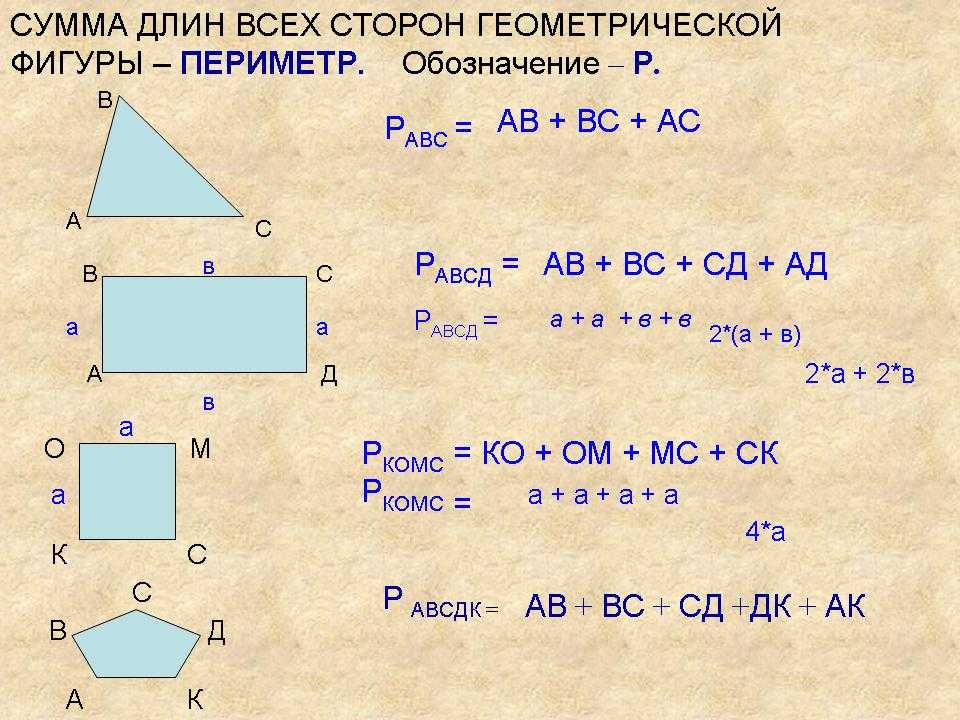 см – 24 кв. см

= 56 квадратных см

Оценка

Найдите площадь неправильной фигуры

Упражнение:

Найдите площадь фигуры, показанной ниже.

1.

2.

3.

4.

5.

Что мы узнали:

• Площадь поверхности или плоской фигуры — это количество квадратных единиц, необходимое для покрытия поверхности или цифра
• Площадь квадрата = S x S
• Площадь прямоугольника = Длина x Ширина
• Площадь измеряется в стандартных единицах
• Чтобы найти площадь неправильной формы
• Разбейте большую площадь на более мелкие части.
• Ищите возможности, в которых меньшие формы являются частью большей формы.
• Разделите большую площадь на меньшие прямоугольники и найдите площадь.

Подведем итоги:

Чтобы найти площадь неправильной формы, первое, что нужно сделать, это разделить неправильную форму на правильные формы, которые вы можете распознать, такие как треугольники, прямоугольники, круги, квадраты и так далее.

Затем найдите площади этих отдельных фигур и сложите их.

Как найти площадь неправильной формы? Определение, примеры, факты

Площадь неправильных форм

Неправильные формы представляют собой многоугольники с пятью или более сторонами различной длины. Эти формы или фигуры можно разложить на треугольники, квадраты и четырехугольники для оценки площади.

Некоторые примеры неправильной формы:

Предметы повседневной жизни неправильной формы

Вычисление площади неправильной формы:

Подходы к оценке площади неправильной формы:

Оценка площади с использованием единичных квадратов и неправильные четырехугольники. В этом методе разделите фигуру на единичные квадраты. Общее количество единичных квадратов, попадающих в фигуру, определяет общую площадь.

Рисунок: Некоторые примеры неправильной формы

Считайте квадрат как «1», если заштрихованная область покрывает более половины при расчете площади для более точной оценки.

Рисунок: Для неправильной формы подсчитайте квадраты с оранжевой и желтой кодировкой как 1.

На следующем рисунке подсчитайте площадь, подсчитав единичные квадраты, что равно 6. Если мы обозначим каждую единицу квадрата в сантиметрах , площадь будет 6 см2.

Рисунок: Расчет площади неправильной формы с изогнутыми краями

• Разделение неправильной формы на две или более правильных фигур

Используйте этот метод для неправильных форм, которые представляют собой комбинацию треугольников и многоугольников. Используйте предопределенные формулы для расчета площади таких фигур и сложите их вместе, чтобы получить общую площадь.

Например, неправильную форму мы делим несколькими ребрами на треугольник и три многоугольника.

Общая площадь фигуры определяется как:

⇒ Площадь = Площадь (ABIM) + Площадь (BCGH) + Площадь (CDEF) + Площадь (JKL)

⇒ Площадь = (AB × BI) + (BC × CG) + (CD × DE) + ( ¹ ⁄ ₂ × LJ × KO)

⇒ Площадь = (10 × 5) + (3 × 3) + (2 × 2) + ( ¹ ⁄ ₂ × 4 × 4) 

⇒ Площадь = 50 + 9 + 4 + 8

⇒ Площадь = 71 см2

• 900 кривые двух или более правильных форм

В этом методе можно разложить неправильную форму на несколько квадратов, треугольников или других четырехугольников.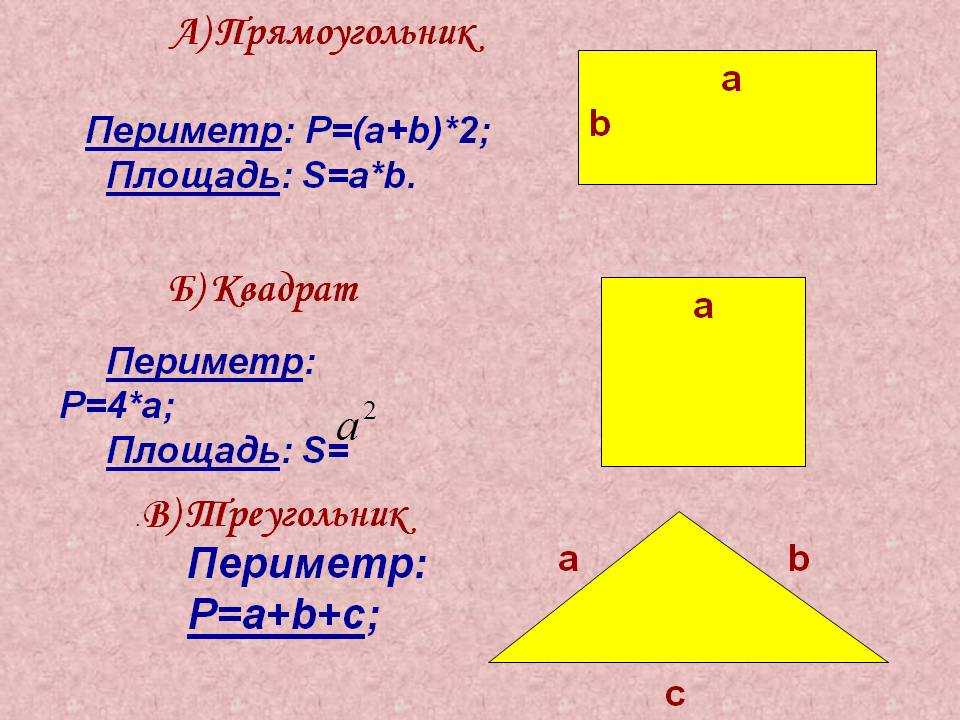 В зависимости от формы и изгибов часть фигуры может быть также кругом, полукругом или квадрантом.

Следующая фигура представляет собой неправильную форму с 8 сторонами, включая одну кривую. Определить неизвестные величины по заданным размерам сторон. Разложите фигуру на два прямоугольника и полукруг.

Площадь формы ABCDEF равна:

Площадь (ABCDEF) = Площадь (ABCG) + Площадь (GDEF) + Площадь (aob)

Площадь = (AB × AG) + (GD × DE) + ( ¹ ⁄ ₂ × π ​​× ob ² )

Площадь = (3 × 4) + (10 × 4) + ( ¹ ⁄ ₂ × 3,14 × 1 ² )

Площадь = 12 + 40 + 1,57

Площадь = 53,57 см архитектура и разметка сельскохозяйственных полей. Мы применяем концепцию в раскрое тканей согласно заданному дизайну. В старших классах эта техника закладывает основу для более сложных тем, таких как вычисление объема, рисование конических сечений и фигур эллиптической формы.

Забавный факт . Многоугольники Танграма являются древними примерами геометрических фигур и могут создавать более 6500 форм.

Родственные игры

• Квадрат
• Прямоугольник
• Треугольник
• Круг
• Площадь
• Неправильные и правильные формы

Связанные рабочие листы

Практические задачи

1

Лист был обведен на миллиметровой бумаге. В нем 10 клеток полностью покрыты, 12 клеток покрыты более чем наполовину и 14 клеток покрыты менее чем наполовину. Какова будет площадь листа?

29 квадратов

16 квадратов

22 квадрата

23 квадрата

Правильный ответ: 22 квадрата
Полностью закрытые квадраты считаются как есть. Каждая более чем наполовину закрытая клетка считается за 1 клетку. Менее чем наполовину закрытые квадраты считаются как 0 каждый.
Таким образом, у нас есть 10 $ + (1 × 12) + (0 × 14) = 10 + 12 = 22 $ квадратных единиц.

2

Какова площадь поля, имеющего форму двух прямоугольников со следующими размерами: Прямоугольник 1: l = 5, w = 6 Прямоугольник 2: l = 8, w = 5

48 кв. см

24 кв. см

70 кв. см

10 кв. см

Правильный ответ: 70 кв. см
Площадь прямоугольника 1 = 5 × 6 = 30 кв.см.
Площадь прямоугольника 2 = 8 × 5 = 40 кв.см
Площадь поля = площадь прямоугольника 1 + площадь прямоугольника 2
= 30 + 40 = 70 кв.см.

3

Чтобы найти площадь неправильной формы, мы сначала разобьем неправильную форму на обычные формы. Затем мы находим площадь каждой фигуры и ___ их.

Умножить

Сложить

Вычесть

Разделить

Правильный ответ: Сложить
Чтобы найти площадь неправильной формы, мы сначала разбиваем фигуру на обычные фигуры. Затем мы находим площадь каждой фигуры и складываем их. Например, если неправильный многоугольник состоит из квадрата и треугольника, то: Площадь неправильного многоугольника = Площадь квадрата + Площадь треугольника.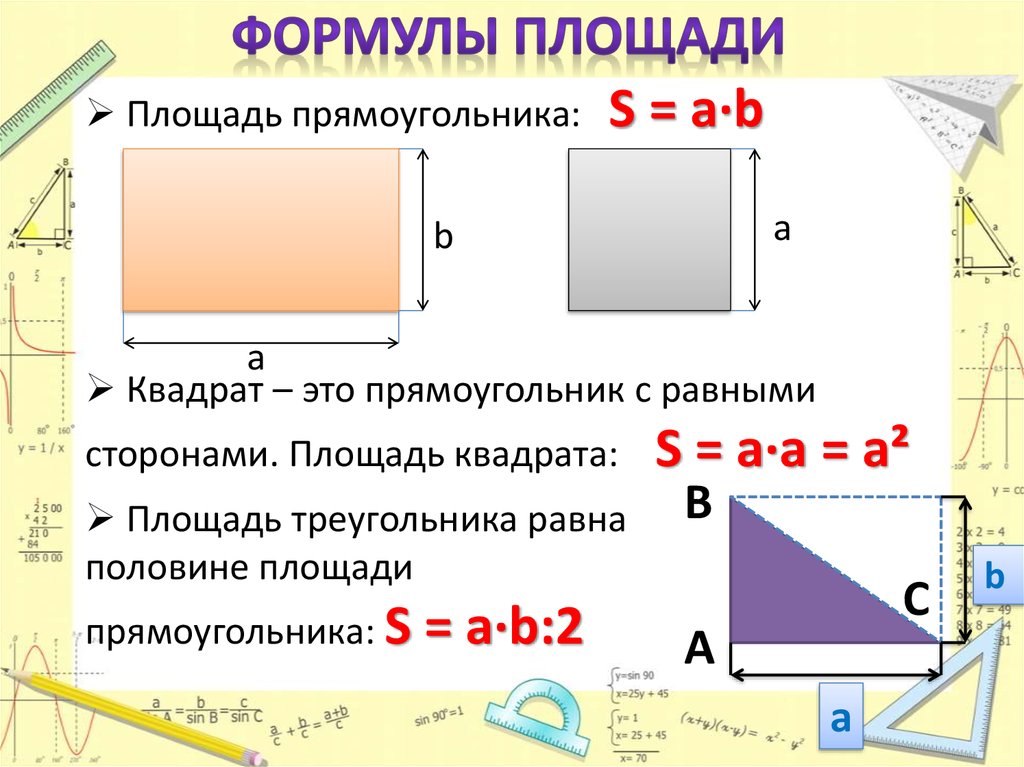

4

Какова площадь неправильного многоугольника, состоящего из 2 квадратов следующих размеров? Квадрат 1: сторона = 5 см Квадрат 2: сторона = 3 см

25 кв. см

34 кв. см

9 кв. см

16 кв. см

Правильный ответ: 34 кв. см
Площадь квадрата 1 = 5 × 5 = 25 кв. см.
Площадь квадрата 2 = 3 × 3 = 9 кв. см.
Площадь неправильного многоугольника = площадь квадрата 1 + площадь квадрата 2 = 25 + 9 = 34 квадратных см.

Часто задаваемые вопросы

Как найти площадь неправильной формы?

Неправильную форму можно разложить на известные многоугольники. Тогда площадь неправильной формы равна сумме площадей каждого из этих многоугольников. Если неправильная форма имеет изогнутые края и невозможно разложить всю форму на известные многоугольники, то лучшим подходом будет оценка площади.

I s Есть ли какая-нибудь формула для нахождения областей неправильной формы?

Нет, общей формулы для расчета площади неправильной формы не существует, потому что стороны могут быть разной длины и кривизны.