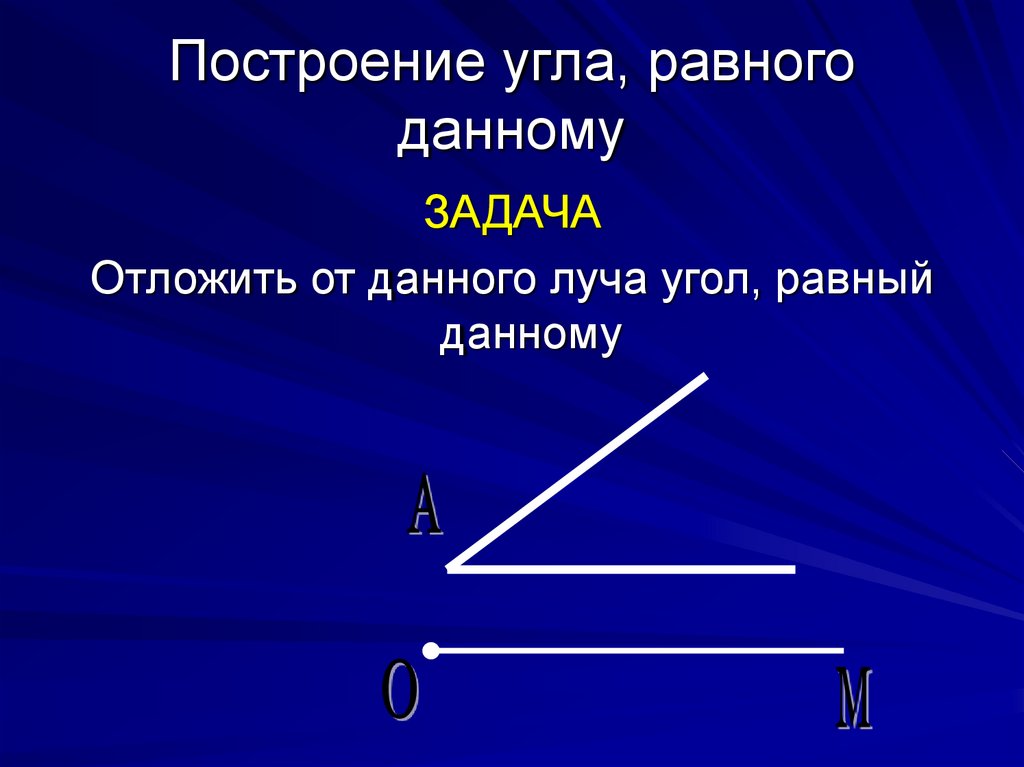
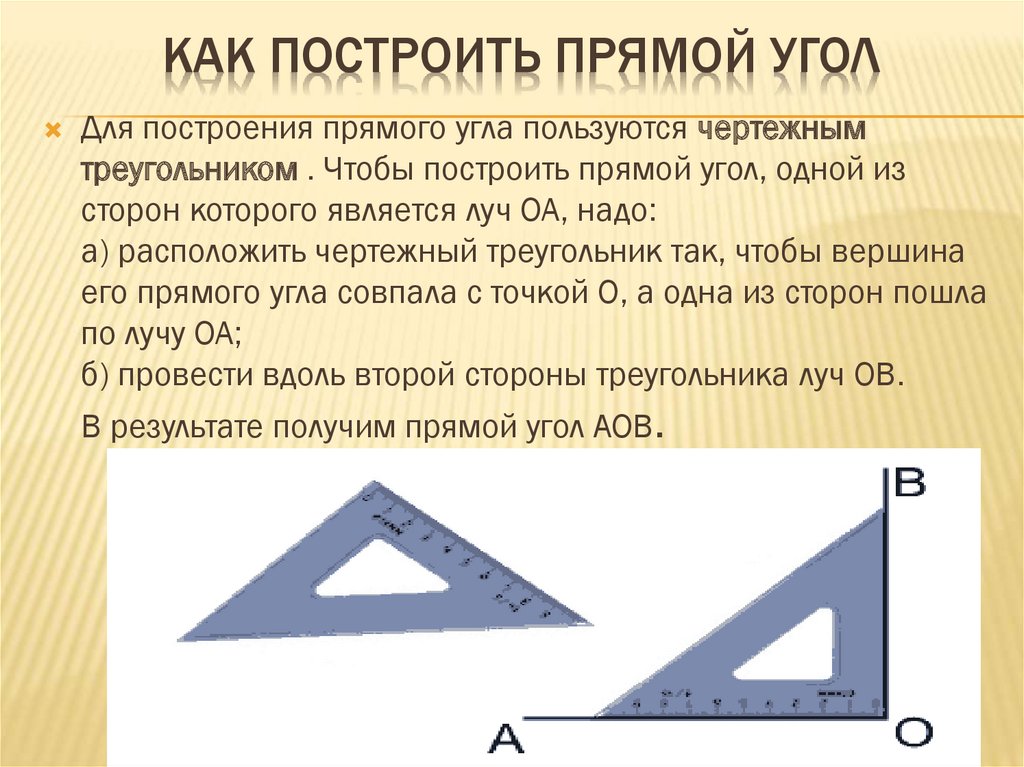
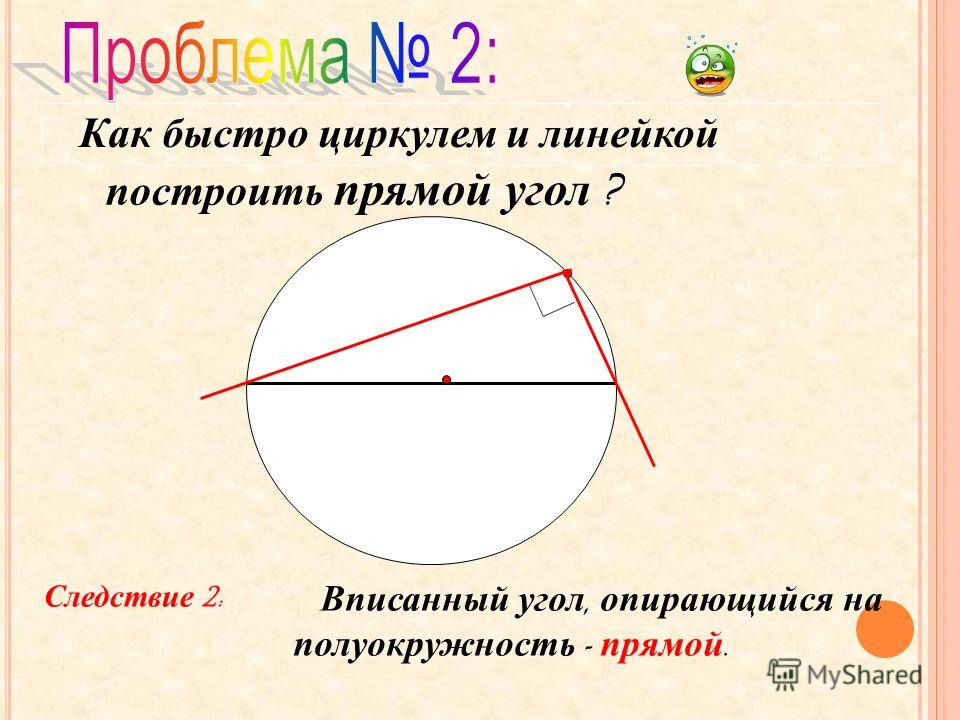
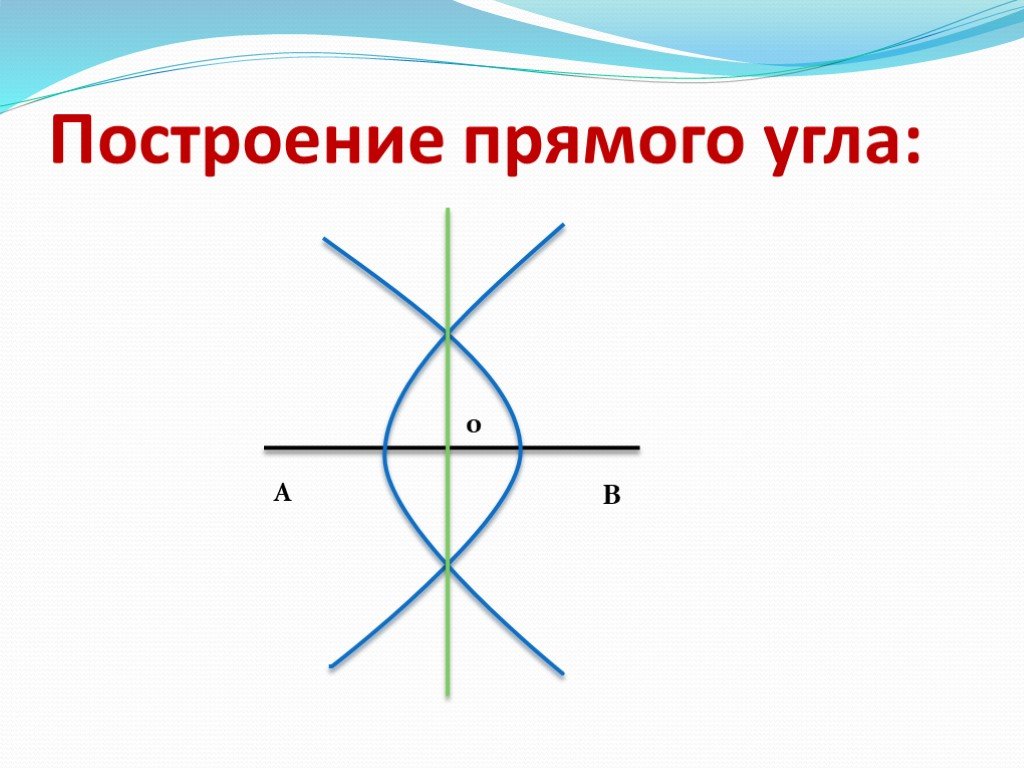
Как проверить прямой угол без угольника
Сразу перейти к калькулятору
При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.
Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.
Теорема Пифагора
Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:
a²+b²=c²
Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза.
Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем
размечать прямые углы, а также проверять их.
Следовательно, сторона c — гипотенуза.
Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем
размечать прямые углы, а также проверять их.
Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!
А теперь применим теорему на практике.
Проверка прямого угла
Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером
в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены —
это стены, расположенные друг к другу под прямым углом 90°.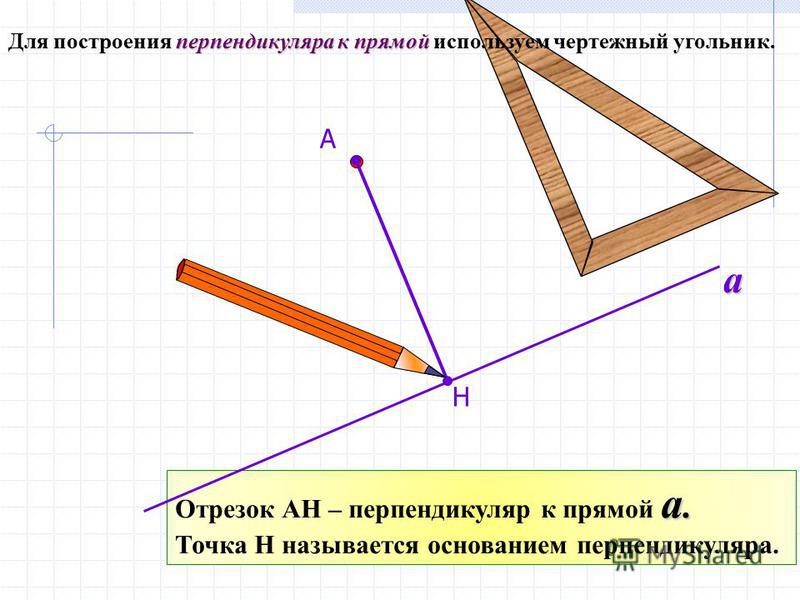
Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.
Калькулятор расчета диагонали прямого угла
Внимание! Для работы калькулятора необходимо включить поддержку JavaScript в вашем браузере!
Длина aДлина b
Диагональ c
Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же,
не на всех мобильных устройствах калькуляторы умеют извлекать его.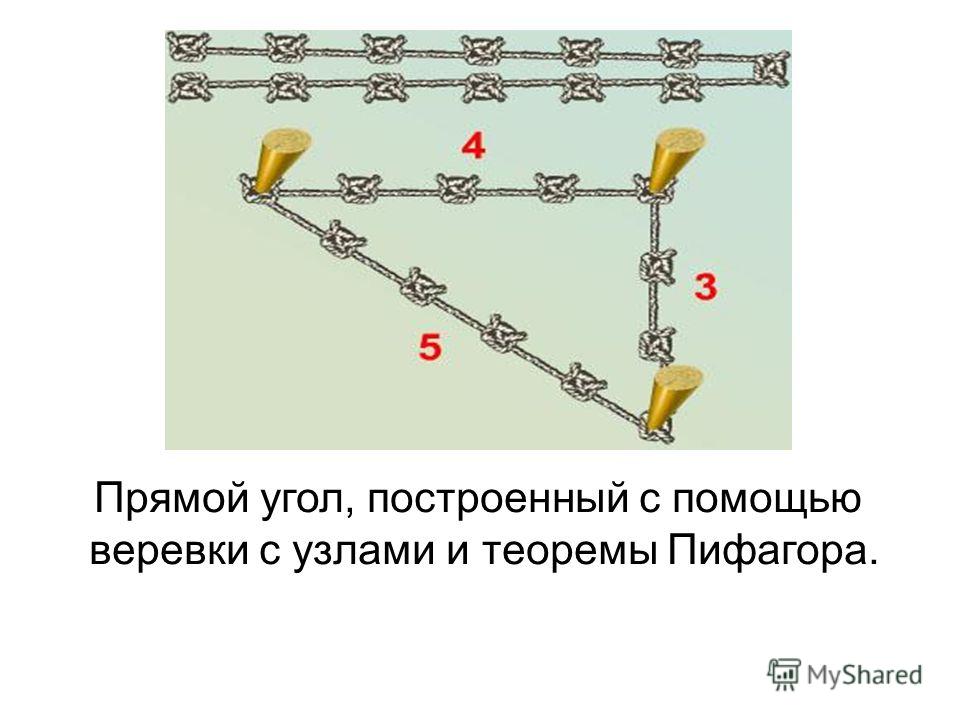 Поэтому можно пользоваться упрощенным методом. Нужно
лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у
прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого
метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны
быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать
о первоначальном способе совсем — в некоторых случаях он очень актуален.
Поэтому можно пользоваться упрощенным методом. Нужно
лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у
прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого
метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны
быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать
о первоначальном способе совсем — в некоторых случаях он очень актуален.
Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое
нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из
понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров
не даст отклонения в один целый градус.
в несколько миллиметров
не даст отклонения в один целый градус.
Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.
Как разметить прямой угол рулеткой
Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.
Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся
последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на
количество метров в отрезке А-Б.
Как разметить острый угол
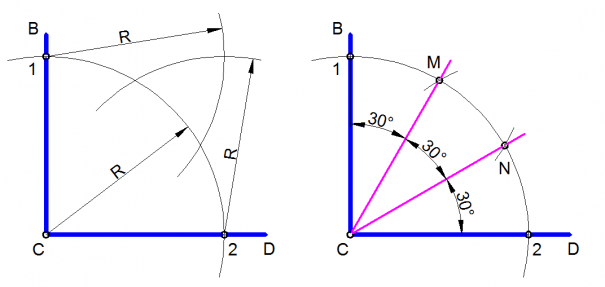
Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.
Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет
вопросов как размечать и проверять прямые углы.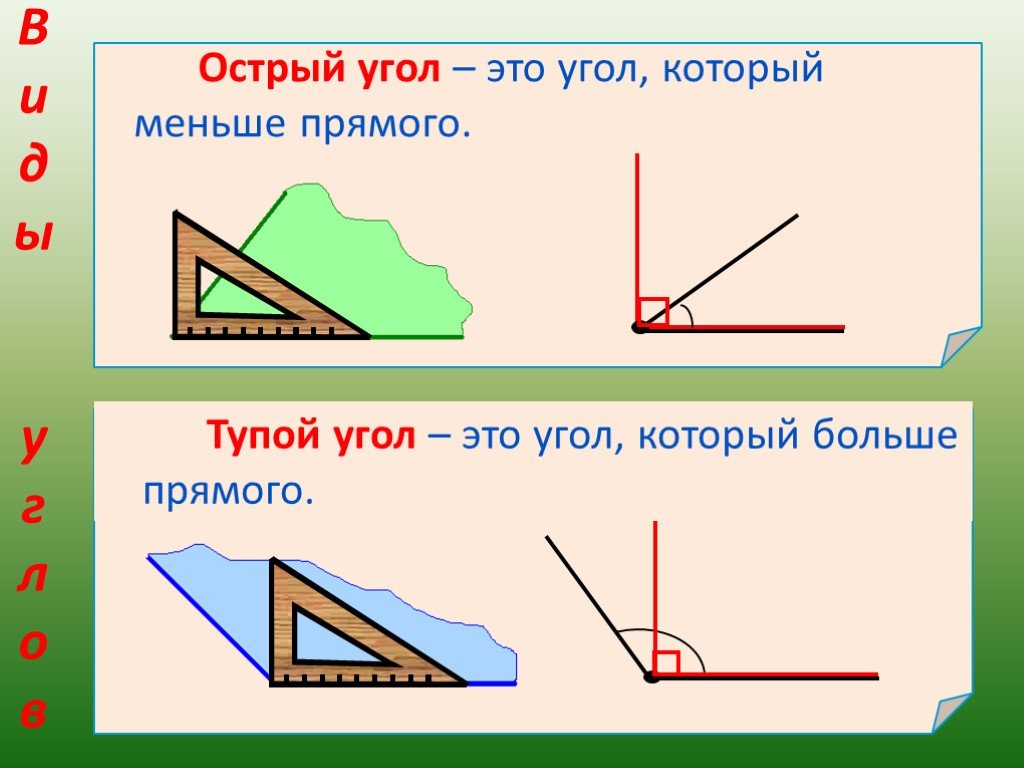 Стоит добавить, что уметь делать это должен любой отделочник или
строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.
Стоит добавить, что уметь делать это должен любой отделочник или
строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.
Смотрите также другие статьи
Что такое угол? Определение, виды, как обозначают, примеры
Поможем понять и полюбить математику
Начать учиться
Знания школьной геометрии пригодятся в самых неожиданных ситуациях: во время ремонта, при рисовании граффити или чтобы нарезать пирог. В этой статье узнаем все про углы.
Определение угла
Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.
Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.
Если нам дана прямая a на плоскости, и на ней есть некоторая точка O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.
Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:
Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.
Что такое вершина и стороны угла
В математике существует специальный символ для обозначения угла, вот он: ∠.
Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.
Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA. Также можно назвать угол одной большой буквой, которая указывает на его вершину, например: ∠O.
Иногда встречается обозначение в виде цифр — так тоже можно.
Для наглядности — все способы обозначения углов:
Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:
Единица измерения углов — градусы. Символ для обозначения градуса угла: °.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Виды углов
Есть разные типы углов и у каждого своё название:
- острый
- прямой
- тупой
- развернутый
- выпуклый
- полный
Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.
Прямой угол — это угол, стороны которого перпендикулярны друг другу.
Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:
На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.
Острый угол — это угол, который меньше прямого угла, то есть < 90°.
Развернутый угол — это открытый угол, который образован двумя лучами и равен сумме двух прямых углов. Развернутый угол равен 180°. Как выглядит развернутый угол, показано на первой картинке.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Неразвернутый угол — это любой угол, который не является развернутым, то есть не равен 180°.
Тупой угол — это угол, который больше прямого угла, но меньше развернутого:
90° < тупой угол < 180°.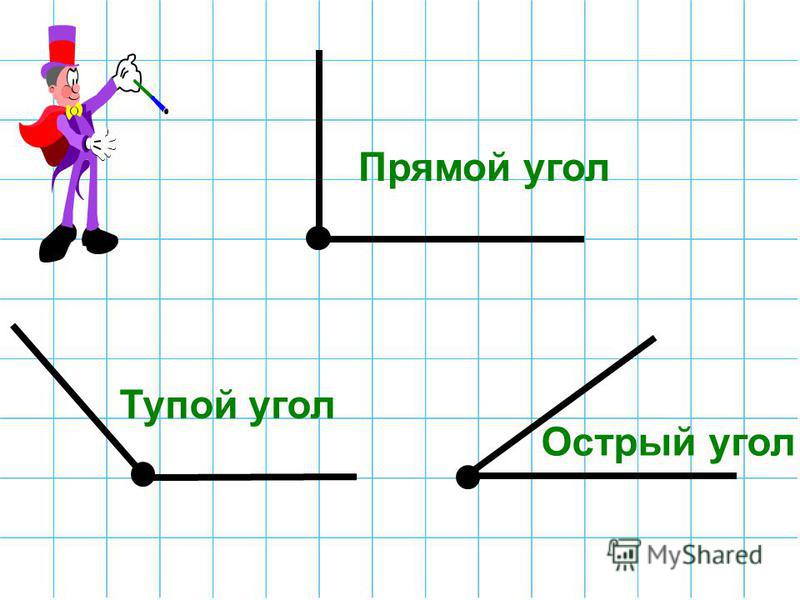
Выпуклый угол — это угол, который больше развернутого угла, но меньше полного:
180° < выпуклый угол < 360°.
Полный угол — это угол, обе стороны которого совпадают с одним лучом. Он равен сумме четырех прямых углов, то есть = 360°.
Прилежащие углы — это пара углов с общей вершиной и стороной, другие стороны при этом лежат по разные стороны от общей стороны.
На картинке мы видим два прилежащих угла ∠AOB и ∠BOC, общую вершину O и общую сторону OB.
Можно сформулировать определение по-другому: если из вершины любого угла провести луч, разделяющий угол на два, то образованные углы будут прилежащими.
Чтобы найти угол, который разделен лучом, нужно сложить полученные углы: ∠AOB = ∠AOC + ∠COB. Из этого можно выделить следующие верные разности:
- ∠AOC = ∠AOB − ∠COB,
- ∠COB = ∠AOB − ∠AOC.

Запоминаем!
Угол называется прямым, если он равен 90°, острым, если он меньше 90°, тупым, если он больше 90°, но меньше 180°. Развернутый угол равен 180°.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Сравнение углов
Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:
При этом развернутые углы всегда являются равными.
Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:
- Вершину 𝐵 одного угла совмещаем с вершиной 𝑁 другого угла.

- Сторону 𝐵𝐴 одного угла накладываем на сторону 𝑁𝑀 другого угла так, чтобы стороны 𝐵𝐶 и 𝑁𝐾 располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.
Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶<∠𝑀𝑁𝐾.
Сравнить углы можно также, измерив их величины. Для этого понадобится специальный инструмент для построения и измерения углов — транспортир. Вот как он выглядит:
Как правильно измерять углы
Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Он обозначается так: °.
Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.
Минута — 1/60 часть градуса. Обозначается ´.
Секунда — 1/60 часть минуты. Обозначается ´´.
Градус состоит из 3600 секунд, то есть: 1° = 60´ = 3600´´.
Как происходит измерение угла: сначала измеряют стороны угла, а после — его внутреннюю область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.
Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.
На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠AOB = ∠AOC + ∠COD + ∠DOB = 45° + 30° + 60° = 135 °.
Равные углы имеют равную градусную меру.
Обозначение углов на чертеже
Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать углы и прочие фигуры, придумали даже отдельное направление — геометрический чертеж.
Задачи с углами могут быть разными, и не всегда есть возможность правильно изобразить и отметить угол. Вот что важно запомнить при обозначении лучей и углов:
- Равные углы обозначают одинаковым количеством дуг.
- Неравные углы обозначают разным количеством дуг, чтобы они отличались между собой.
На чертеже отмечены три неравных угла:
Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.
Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом не обязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.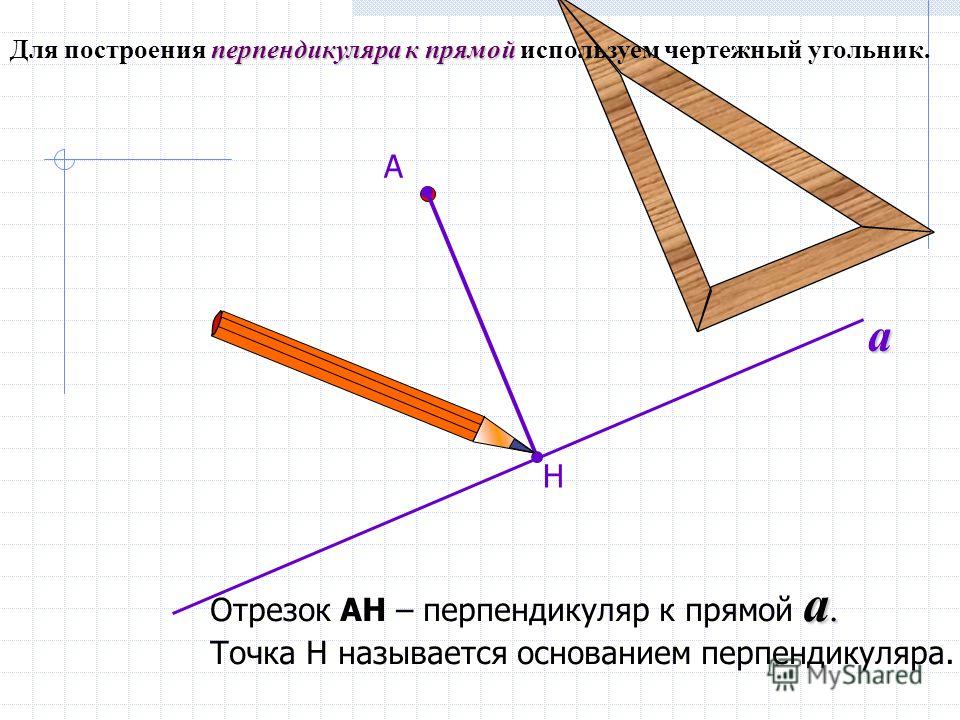
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
251.4K
Наибольший общий делитель (НОД), свойства и формулы
К следующей статье
202.4K
Неполные квадратные уравнения
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Как нарисовать прямой угол?
Прямой угол — это угол, равный 90 градусам. Он образован двумя линиями, которые перпендикулярны друг другу, образуя букву «L».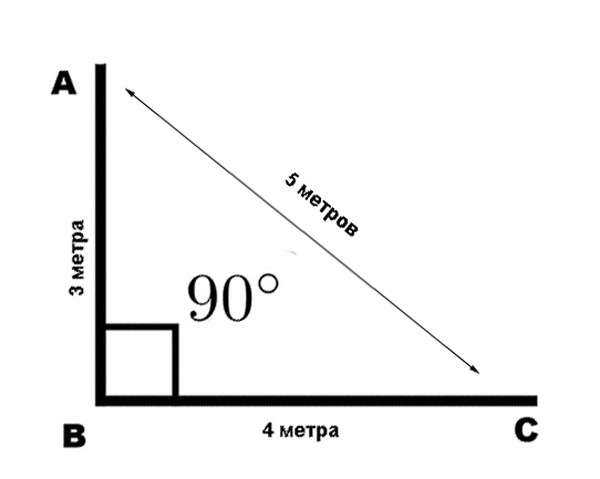 Умение рисовать прямой угол важно в различных областях, включая искусство, строительство и геометрию.
Умение рисовать прямой угол важно в различных областях, включая искусство, строительство и геометрию.
В искусстве прямой угол часто используется для создания композиций с четкими четкими линиями и для создания перспективы. В строительстве важно уметь точно рисовать прямые углы, чтобы здания и другие конструкции были правильно выровнены и устойчивы.
В геометрии понимание того, как чертить и измерять прямые углы, необходимо для решения задач и понимания свойств фигур. В целом, способность точно рисовать прямой угол — полезный навык во многих различных ситуациях.
Как нарисовать прямой угол
Инструменты, необходимые для рисования прямого угла
- Компас
- Каркасный квадрат
- Каркасный квадрат
- Линейка и угольник/рамочный угольник
- Ручка
- Карандаш
- Маркер
Чтобы нарисовать прямой угол, следуйте этим методам
Способ 1: Использование циркуля
Чтобы нарисовать прямой угол с помощью циркуля, выполните следующие действия:
- Поместите острие компаса на точку там, где вы хотите, чтобы был правильный угол.
 Это точка, где будет образовываться угол.
Это точка, где будет образовываться угол. - Нарисуйте дугу с помощью компаса. Следите за тем, чтобы расстояние между двумя точками компаса оставалось таким же, как вы рисуете дугу.
- Не изменяя расстояния между двумя точками компаса, поместите точку на пересечении двух дуг и нарисуйте другую дугу. Это создаст еще одну линию, пересекающую первую дугу под прямым углом.
- Точка, в которой вторая дуга пересекает первую дугу, является прямым углом. Вы можете убедиться в этом, измерив угол транспортиром или проверив, что линии образуют идеальную форму буквы «L».
Не забывайте поддерживать постоянное расстояние между двумя точками компаса на протяжении всего процесса, чтобы обеспечить точное построение угла. Попрактикуйтесь в этом процессе несколько раз, чтобы почувствовать его и улучшить свою точность.
Советы и рекомендации по получению точных измерений:
- Прежде чем начать рисовать, убедитесь, что компас настроен на правильную ширину.

- Держите компас ровно, рисуя дуги, чтобы убедиться, что они имеют одинаковую ширину.
- С помощью линейки или линейки соедините точки пересечения дуг, чтобы создать прямую линию.
- Дважды проверьте угол с помощью транспортира, чтобы убедиться, что он составляет ровно 90 градусов.
- Попрактикуйтесь в использовании компаса, чтобы начертить углы разной ширины, чтобы улучшить свои навыки и точность.
Способ 2. Использование угольника и линейки
Чтобы нарисовать прямой угол с помощью угольника и линейки, выполните следующие действия:
- Нарисуйте прямую линию с помощью линейки. Это будет одна сторона прямого угла.
- Поместите квадрат так, чтобы одна сторона была выровнена с линией, которую вы только что нарисовали, а другая сторона была перпендикулярна ей. Сторона квадрата, перпендикулярная линии, должна касаться линии в той точке, где должен быть прямой угол.
- Используйте линейку, чтобы провести линию вдоль стороны квадрата, перпендикулярную первой линии.
 При рисовании следите за краем квадрата, чтобы линия была идеально перпендикулярна первой линии.
При рисовании следите за краем квадрата, чтобы линия была идеально перпендикулярна первой линии.
Следуя этим шагам, вы сможете точно и точно нарисовать прямой угол. Не забудьте выровнять квадрат по первой линии, когда рисуете вторую линию, чтобы убедиться, что угол сформирован правильно. Попрактикуйтесь в этом процессе несколько раз, чтобы почувствовать его и улучшить свою точность.
Преимущества использования этого метода:
- Квадрат — это инструмент, который специально разработан для рисования прямых углов, поэтому он очень точен.
- Он прост в использовании, так как требует лишь базовых знаний по геометрии.
- Это полезно для базовой геометрии, искусства и дизайна, а также для строительных проектов.
- Не требует специальных инструментов или оборудования.
- Размер угла регулируется перемещением угольника и линейки вдоль линии.
Обратите внимание, что вы можете использовать комбинированный квадрат, который представляет собой квадрат с линейкой, прикрепленной к одной стороне, чтобы сделать этот процесс еще проще.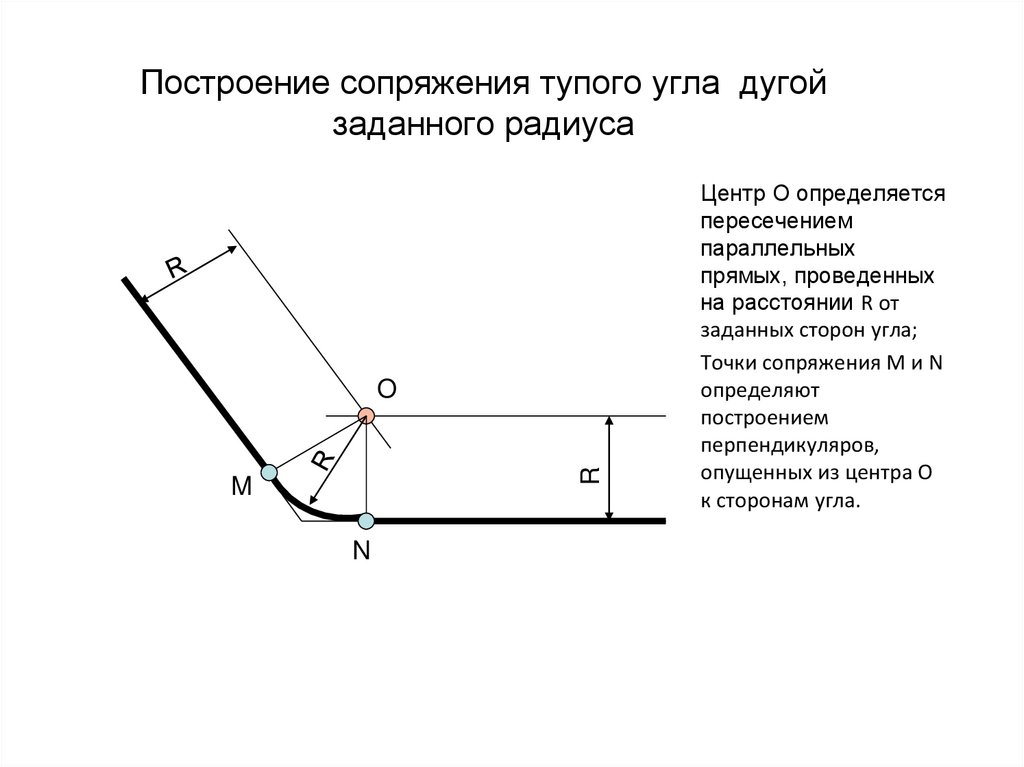
Метод 3: использование линейки и транспортира
Пошаговые инструкции по построению прямого угла с помощью линейки и транспортира:
- Начните с рисования прямой линии. Это будет одна сторона прямого угла.
- Затем с помощью линейки (например, линейки) начертите линию, перпендикулярную первой линии. Это будет другая сторона прямого угла.
- Наконец, с помощью транспортира измерьте угол, образованный пересечением двух линий. Он должен измерять ровно 90 градусов.
Советы и рекомендации по получению точных измерений:
- Убедитесь, что линейка выровнена, когда проводите линии, чтобы они были идеально перпендикулярны.
- Дважды проверьте угол с помощью транспортира, чтобы убедиться, что он составляет ровно 90 градусов.
- Попрактикуйтесь в рисовании углов разной ширины, чтобы улучшить свои навыки и точность.
- При использовании транспортира совместите основание транспортира с одной из линий, образующих угол, а вершина угла должна находиться на отметке 0 градусов.

- При использовании линейки используйте одну из кромок, а не угол, чтобы нарисовать угол, чтобы сделать его более точным.
- Вы также можете использовать метод 3-4-5 для рисования прямого угла без транспортира, это простой и легкий метод.
Метод 2: использование метода 3-4-5
Это простой метод построения прямого угла без использования транспортира. Он основан на том, что в прямоугольном треугольнике, если один катет имеет длину 3 единицы, а другой катет — 4 единицы, то гипотенуза (прямая, противоположная прямому углу) будет иметь длину 5 единиц. Нарисовав отрезки такой длины и соединив их под прямым углом, вы можете создать прямой угол.
Пошаговые инструкции, как нарисовать прямой угол методом 3-4-5:
- Нарисуйте отрезок длиной 3 единицы.
- Нарисуйте еще один отрезок длиной 4 единицы так, чтобы он соединился с первым отрезком под прямым углом.
- Нарисуйте отрезок длиной 5 единиц так, чтобы он соединился со вторым отрезком под прямым углом.

Преимущества использования этого метода:
- Это просто и понятно.
- Не требует специальных инструментов или оборудования.
- С его помощью можно быстро и легко нарисовать прямой угол без транспортира или другого измерительного инструмента.
- Его легко запомнить, так как метод 3-4-5 основан на простых соотношениях, которые вы легко можете вспомнить.
- Это полезно для базовой геометрии и строительства.
Обратите внимание, что этот метод можно использовать только для рисования прямого угла определенного размера (3-4-5). Если вам нужно нарисовать прямой угол другого размера, вам нужно будет использовать другие соотношения длин сторон.
Вот таблица, в которой сравниваются различные инструменты и методы для рисования прямоугольного угла
| Инструмент/Метод | Преимущества | Диспасный | Может быть трудно получить точный результат, если расстояние между точками компаса не поддерживается постоянным | |
|---|---|---|---|---|
| Квадрат | Простота в использовании и возможность точного измерения | Позволяет рисовать только прямые углы | ||
| Рамочный угольник | Прост в использовании и позволяет выполнять точные измерения | Позволяет рисовать только прямые углы | ||
| Линейка и угольник/рамочный угольник | 82 | 82 | 82 использование и позволяет проводить точные измерения | Требуется использование нескольких инструментов |
| Ручка | Позволяет создавать постоянные линии | Может быть трудно получить точный результат без использования таких инструментов, как циркуль, угольник , или обрамляющий квадрат | ||
| Карандаш | Позволяет создавать легко стираемые линии | Может быть трудно получить точный результат без использования таких инструментов, как циркуль, угольник или угольник создание жирных постоянных линий | Может быть трудно получить точный результат без использования таких инструментов, как циркуль, угольник или |
Часто задаваемые вопросы
Вот некоторые дополнительные часто задаваемые вопросы о рисовании прямых углов:
Можно ли нарисовать прямой угол с помощью одной линейки?
Да, можно нарисовать прямой угол, используя только линейку, но может быть труднее получить точный результат без инструмента, в который встроен угол 90 градусов, например, угольника или рамки. квадрат. Чтобы нарисовать прямой угол с помощью линейки, вы можете провести прямую линию, а затем с помощью угольника или обрамляющего угольника убедиться, что вторая линия перпендикулярна первой. Затем с помощью линейки можно провести вторую линию вдоль стороны квадрата или обрамить квадрат, перпендикулярный первой линии.
квадрат. Чтобы нарисовать прямой угол с помощью линейки, вы можете провести прямую линию, а затем с помощью угольника или обрамляющего угольника убедиться, что вторая линия перпендикулярна первой. Затем с помощью линейки можно провести вторую линию вдоль стороны квадрата или обрамить квадрат, перпендикулярный первой линии.
Можно ли нарисовать прямой угол от руки?
Можно нарисовать прямой угол от руки, но получить точный результат без использования таких инструментов, как циркуль, угольник или угольник, может быть сложно. Если вы хотите попробовать нарисовать прямой угол от руки, вы можете начать с рисования прямой линии, а затем попытаться нарисовать вторую линию, перпендикулярную первой. Возможно, вам будет полезно сначала потренироваться рисовать прямые углы с помощью инструментов, чтобы почувствовать правильный угол и повысить точность.
Можно ли нарисовать прямой угол ручкой?
Да, вы можете использовать перо, чтобы нарисовать прямой угол, но получить точный результат без использования таких инструментов, как циркуль, угольник или угольник, может быть труднее. Если вы хотите попробовать нарисовать прямой угол ручкой, вы можете использовать линейку, чтобы нарисовать прямую линию, а затем использовать угольник или обрамляющий угольник, чтобы убедиться, что вторая линия перпендикулярна первой. Затем с помощью пера можно провести вторую линию вдоль той стороны квадрата или обрамляющего квадрата, которая перпендикулярна первой линии.
Если вы хотите попробовать нарисовать прямой угол ручкой, вы можете использовать линейку, чтобы нарисовать прямую линию, а затем использовать угольник или обрамляющий угольник, чтобы убедиться, что вторая линия перпендикулярна первой. Затем с помощью пера можно провести вторую линию вдоль той стороны квадрата или обрамляющего квадрата, которая перпендикулярна первой линии.
Можно ли нарисовать прямой угол карандашом?
Да, вы можете использовать карандаш, чтобы нарисовать прямой угол, и с карандашом может быть проще получить точный результат, потому что вы можете стирать и корректировать линии, если это необходимо. Вы можете использовать те же методы для рисования прямого угла карандашом, что и ручкой, используя линейку и угольник или обрамляющий угольник для обеспечения точности.
Можно ли нарисовать прямой угол маркером?
Да, вы можете использовать маркер, чтобы нарисовать прямой угол, но получить точный результат без использования таких инструментов, как циркуль, угольник или угольник, может быть труднее. Если вы хотите попробовать нарисовать прямой угол маркером, вы можете использовать линейку, чтобы нарисовать прямую линию, а затем использовать угольник или обрамляющий угольник, чтобы убедиться, что вторая линия перпендикулярна первой. Затем маркер можно использовать для рисования второй линии вдоль той стороны квадрата или обрамляющего квадрата, которая перпендикулярна первой линии.
Если вы хотите попробовать нарисовать прямой угол маркером, вы можете использовать линейку, чтобы нарисовать прямую линию, а затем использовать угольник или обрамляющий угольник, чтобы убедиться, что вторая линия перпендикулярна первой. Затем маркер можно использовать для рисования второй линии вдоль той стороны квадрата или обрамляющего квадрата, которая перпендикулярна первой линии.
Примечание редактора
Чтобы построить прямой угол без транспортира, вы можете использовать циркуль. Для этого поместите острие циркуля в точку, где должен быть прямой угол, и начертите дугу. Затем, не меняя расстояния между двумя точками компаса, поместите точку на пересечении двух дуг и начертите другую дугу. Точка, в которой вторая дуга пересекает первую дугу, является прямым углом.
Чтобы нарисовать линию под углом 90 градусов без транспортира, вы также можете использовать линейку и угольник. Сначала проведите прямую линию с помощью линейки. Затем поместите квадрат так, чтобы одна сторона была выровнена с линией, а другая сторона была перпендикулярна ей. С помощью линейки нарисуйте линию вдоль стороны квадрата, перпендикулярную первой линии. это будет 90-градусная линия.
С помощью линейки нарисуйте линию вдоль стороны квадрата, перпендикулярную первой линии. это будет 90-градусная линия.
Можно нарисовать прямоугольный треугольник, используя метод, описанный выше, для построения прямого угла, а затем начертив две линии любой длины, которые пересекаются под прямым углом.
Вместо транспортира для рисования углов можно использовать циркуль или угольник.
Для построения прямого угла в строительстве можно использовать угольник или обрамляющий угольник. Эти инструменты имеют одну сторону, которая составляет 90 градусов, и их можно использовать, чтобы углы были идеально прямыми.
Чтобы шаг за шагом нарисовать угол 90 градусов с помощью компаса, выполните следующие действия:
- Поместите острие компаса в точку, где должен быть угол.
- Нарисуйте дугу.
- Не изменяя расстояния между двумя точками компаса, поместите точку на пересечении двух дуг и нарисуйте другую дугу.
- Точка, в которой вторая дуга пересекает первую дугу, составляет угол 90 градусов.

Чтобы сделать угол под прямым углом, вы можете использовать угольник или обрамляющий угольник, чтобы углы были идеально прямыми.
Угол в 90 градусов выглядит как прямой или прямоугольный угол. Это угол, образованный двумя линиями, перпендикулярными друг другу, образующими букву «L».
Для детей угол 90 градусов можно объяснить как угол, который выглядит как угол коробки. Он образуется, когда две линии встречаются под прямым углом и образуют букву «Т».
Заключение
Подводя итог, можно выделить два основных метода построения прямого угла: с помощью циркуля и с помощью угольника и линейки.
Чтобы нарисовать прямой угол с помощью циркуля, поместите острие циркуля в точку, где должен быть прямой угол, начертите дугу, а затем, не меняя расстояния между двумя точками циркуля, поместите точку на пересечении двух дуг и нарисуйте еще одну дугу. Точка, в которой вторая дуга пересекает первую дугу, является прямым углом.
Чтобы нарисовать прямой угол с помощью угольника и линейки, начертите с помощью линейки прямую линию, поместите угольник так, чтобы одна сторона была на одной линии с линией, а другая сторона перпендикулярна ей, и с помощью линейки начертите линию вдоль стороны квадрата, которая перпендикулярна первой линии.
Чтобы убедиться, что прямой угол нарисован точно, важно тщательно следовать инструкциям и обращать внимание на детали. Сохраняйте постоянное расстояние между точками компаса при использовании компаса и следите за тем, чтобы угольник выровнялся с первой линией при использовании угольника и линейки. Практика рисования прямых углов поможет вам улучшить свои навыки и повысить точность.
В целом, знание того, как рисовать прямой угол, является полезным навыком во многих различных областях, и практика этого навыка может помочь вам повысить точность и аккуратность в вашей работе.
Построение угла 90 градусов — Построение угла 90 градусов с помощью циркуля, транспортира и некоторых решенных примеров.
LearnPracticeDownload
Построение угла 90 градусов s можно выполнить двумя способами — с помощью циркуля и с помощью транспортира. Создание чернового наброска отличается от построения в геометрии. В геометрии под построением мы подразумеваем рисование фигур, линий, углов с более точными измерениями. Нам понадобятся линейка, компас и транспортир. Построение в геометрии всегда начинается с точки. Затем мы расширяемся, чтобы нарисовать отрезок или линию, а затем построить требуемую форму или угол. Угол в геометрии — это пространство между двумя пересекающимися линиями. 90° обозначает прямой угол в геометрии. Иногда возникает необходимость построить углы без использования транспортира. Давайте узнаем, как построить угол 90 градусов в этой статье.
Нам понадобятся линейка, компас и транспортир. Построение в геометрии всегда начинается с точки. Затем мы расширяемся, чтобы нарисовать отрезок или линию, а затем построить требуемую форму или угол. Угол в геометрии — это пространство между двумя пересекающимися линиями. 90° обозначает прямой угол в геометрии. Иногда возникает необходимость построить углы без использования транспортира. Давайте узнаем, как построить угол 90 градусов в этой статье.
| 1. | Построение угла 90° с помощью компаса |
| 2. | Построение угла 90° с транспортиром |
| 3. | Решенные примеры |
| 4. | Практические вопросы |
| 5. | Часто задаваемые вопросы о построении угла 90° |
Построение угла 90 градусов с помощью компаса
В этом разделе вы узнаете, как построить угол 90 градусов с помощью циркуля. Шаги для построения угла 90 градусов следующие.
Шаги для построения угла 90 градусов следующие.
Шаг 1: Нарисуйте отрезок любой длины и обозначьте его концы как A и B.
Шаг 2: С помощью циркуля и любой ширины в качестве радиуса и с A в качестве центра нарисуйте дугу, которая пересекает отрезок AB в точке и обозначьте ее как C.
Шаг 3: С тем же радиусом и с точкой C в качестве центра нарисуйте дугу, которая пересекает предыдущую дугу, и назовите ее D.
Шаг 4: С D в качестве центра и с тем же радиусом нарисуйте другую дугу и назовите ее это как E.
Шаг 5: С таким же радиусом и с D и E в качестве центров нарисуйте две дуги, пересекающие друг друга в точке, и обозначьте их как F.
Шаг 6: Теперь соедините точки F и A. Теперь мы можем наблюдать что ∠FAB = 90°.
Построение угла 90 градусов с транспортиром
Построение угла 90° также можно выполнить с помощью транспортира. Транспортир — это геометрический инструмент, на котором нанесены отметки углов. Давайте рассмотрим шаги, чтобы сделать то же самое.
Транспортир — это геометрический инструмент, на котором нанесены отметки углов. Давайте рассмотрим шаги, чтобы сделать то же самое.
Шаг 1: Нарисуйте отрезок XY любого размера.
Шаг 2: Поместите середину или центр транспортира в точку X. место 90° как Z.
Шаг 4: Соедините точки Z и X. Теперь ∠ZXY измеряет 90°.
Статьи по теме
Ознакомьтесь с некоторыми интересными статьями о построении угла 90°. Нажмите, чтобы узнать больше!
- Геометрия
- Уголки
- Биссектриса угла
- точек и линий
- Биссектрисы перпендикуляра
Решенные примеры построения угла 90 градусов
Пример 1: Постройте биссектрису для отрезка длины AB = 8 единиц и проверьте, равен ли угол, образованный биссектрисой с отрезком, равен 90° или нет.
Решение:
Шаг 1: Нарисуйте отрезок длиной AB = 8 единиц.

Шаг 2: Используя A в качестве центра и более половины длины AB в качестве радиуса, нарисуйте дугу с обеих сторон отрезка AB. Повторите тот же процесс с B в качестве центра и того же радиуса. Отметьте точки пересечения как P и Q.
Шаг 3: Соедините точки P и Q. PQ является серединным перпендикуляром к AB. Кроме того, мы можем заметить, что биссектриса образует угол 90° с отрезком AB.
Пример 2: Какие есть примеры из реальной жизни, где мы можем наблюдать угол 90°?
Решение:
Углы, образованные ветвями ветряной мельницы, часами, показывающими девять часов, и углы, образованные углами прямоугольных окон и дверей, являются некоторыми примерами из реальной жизни, где мы можем наблюдать угол 90°. .
перейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
С Cuemath вы будете учиться визуально и будете удивлены результатами.
Забронировать бесплатный пробный урок
Практические вопросы по построению угла 90 градусов
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о построении угла 90 градусов
Как называется угол 90°?
Угол 90° называется прямым углом. Угол 90° можно построить, отмерив 90° в транспортире или построив серединный перпендикуляр к прямой. Серединный перпендикуляр образует с прямой 90°.
Как построить угол 90 градусов с помощью циркуля и линейки?
Чтобы построить угол 90° с помощью циркуля и линейки, выполните шаги, указанные ниже:
- Нарисуйте линию и обозначьте ее концы как A и B.
- Используя циркуль любой ширины в качестве радиуса и с A в качестве центра, нарисуйте дугу, которая пересекает отрезок AB в точке, и обозначьте ее как C.
- С тем же радиусом и с точкой C в центре нарисуйте дугу, которая пересекает первую дугу, и назовите ее D.

- С D в качестве центра и с тем же радиусом нарисуйте еще одну дугу и назовите ее E.
- С таким же радиусом и с D и E в качестве центра нарисуйте две дуги, пересекающие друг друга, и обозначьте их буквой F.
- Теперь соедините линии F и A. Теперь мы можем заметить, что угол FAB = 90°.
Как построить угол 90 градусов с помощью транспортира и линейки?
Чтобы построить угол 90° с помощью транспортира и линейки, выполните следующие действия:
- Нарисуйте отрезок и обозначьте его как XY.
- Поместите середину или центр транспортира в точку X.
- Начиная с 0° по транспортиру, двигайтесь против часовой стрелки и отметьте точку на месте 90° как Z.
- Соедините точки Z и X. Теперь угол ZXY равен 90°.
Какой угол образует биссектриса?
Угол, образованный серединным перпендикуляром, равен 90°. Биссектриса — это отрезок, который делит отрезок на две равные части, образующие угол 90°.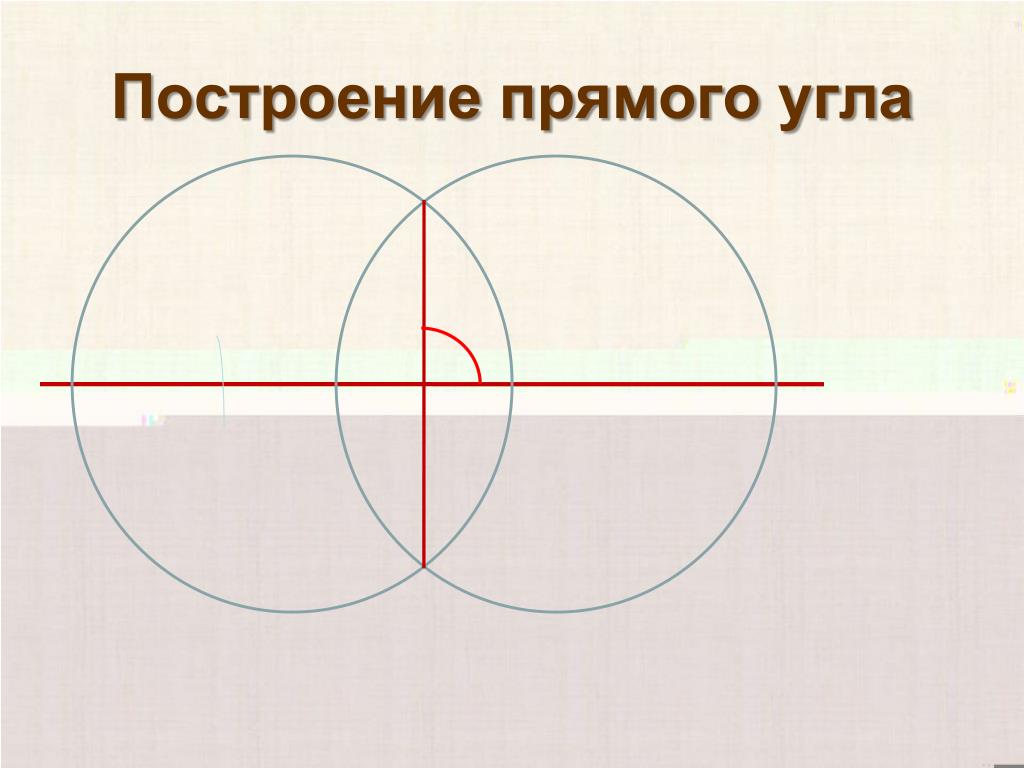

 Это точка, где будет образовываться угол.
Это точка, где будет образовываться угол.
 При рисовании следите за краем квадрата, чтобы линия была идеально перпендикулярна первой линии.
При рисовании следите за краем квадрата, чтобы линия была идеально перпендикулярна первой линии.