Как считать периметр комнаты: Расчет периметра комнаты — онлайн калькулятор

Расчет площади стен под поклейку обоев

Для того чтобы определить стоимость услуг при поклейке обоев частным мастером, необходимо знать общую площадь стен и периметр комнаты. Бывают такие услуги, которые считаются по квадратным метрам, например поклейка или грунтовка. А есть такие услуги, для которых требуется знать погонные метры, например, монтаж плинтуса или поклейка бордюров. Необязательно пользоваться услугами замерщиков, достаточно вспомнить школьную программу по геометрии. Эта информация также поможет при подсчете нужного количества обоев, клея и так далее.

---

Площадь стен = периметр комнаты * на высоту потолка

---

Сначала требуется измерить ширину и длину комнаты. Сразу скажем, что полученные измерения длины и ширины комнаты нужно переводить в метры. К примеру, если длина комнаты 325 сантиметров, то считаем 3,25 метра.

Длина комнаты 4,75 метра
Ширина комнаты 3,25 метра

Вычислим периметр комнаты, который равен сумме всех сторон.

P=(a+b)х2, где a и b – это ширина и длина комнаты.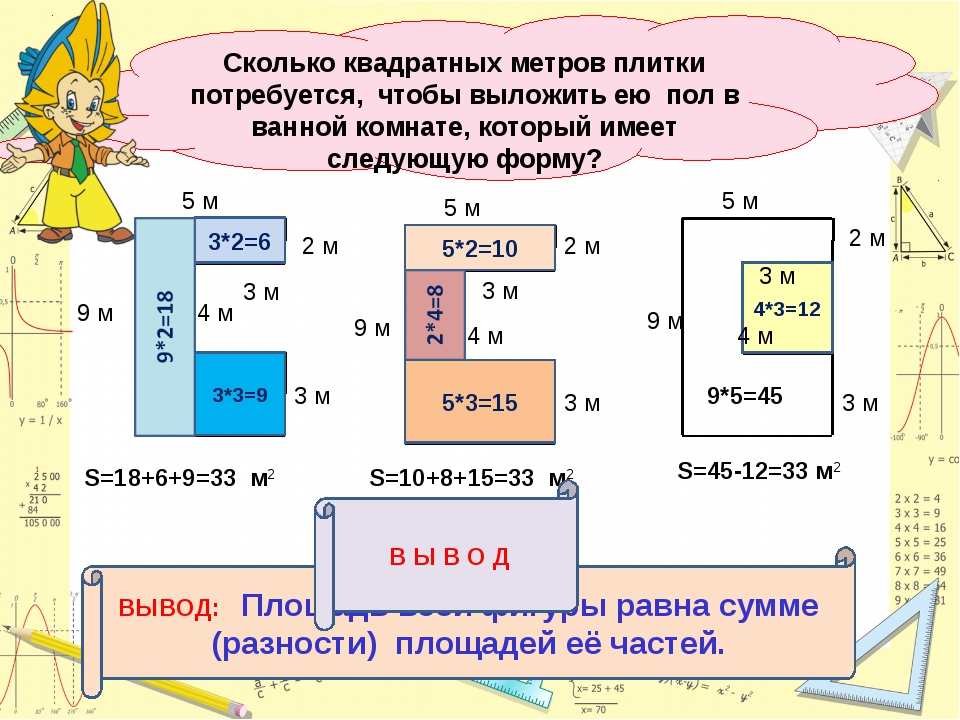

Следовательно (4,75+3,25)х2=16 метров.
Периметр нашей комнаты равен 16 метров. P=16 метров.

Теперь нужно измерить высоту комнаты. Измеряем высоту стены – у нас получилось 2,71 метра.
h=2,71 метра.

Чтобы получить площадь стен, нужно периметр комнаты умножить на высоту стен.

S стен =Pхh, где h-высота стен.
S стен=16х2,71=43,36 метра. 

Площадь стен нашей комнаты 43,36 кв. метра. S=43,36 м².

Из этой цифры нужно вычесть площадь окон и двери – ведь там клеить обои не нужно. У нас в комнате одно окно, площадь которого равна 1,95 м² (1,3м х 1,5м). Площадь двери 1,17 м² (0,61м х 1,92м). Сумма площадей окон и дверей, которые не участвуют в поклейке обоев, равна 3,12 м².

Чистая площадь стен равна 43,36 — 3,12=40,24 м².

В случаях, когда комната нестандартного размера и не похожа на прямоугольник, придется вычислять площадь каждой стены отдельно и потом их суммировать.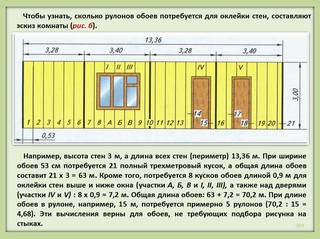

Таблица площадей стен под обои и покраску

Ниже приведена таблица, которая поможет быстро определить площадь стен под поклейку обоев (или покраску). Для расчета показателей использована типовая площадь окон и дверей. Показатели площади стен различаются по высоте потолка помещения:

Площадь помещения, м2	Высота потолка помещения 2,50 м	Высота потолка помещения 2,70 м	Высота потолка помещения 3,0 м
10	29	31	33
11	30,5	32,5	34,5
12	32	34	36
13	33,5	35,5	37,5
14	35	37	39
15	36,5	38,5	40,5
16	38	40	42
17	39,5	41,5	43,5
18	41	43	45
19	42,5	44,5	46,5
20	44	46	48
21	45,5	47,5	49,5
22	47	49	51
23	48,5	50,5	52,5

 

---

Смотрите также:

Цены на поклейку обоев	Цены шпаклевки стен к покраске	Косметический ремонт комнаты

 

 

Как найти периметр прямоугольника — Лайфхакер

Напомним, периметром называют суммарную длину всех сторон. Вычислить её можно по‑разному. Выбирайте формулу в зависимости от известных вам данных.

Зная все или две соседние стороны

Для полноты упомянем простейшие классические формулы.

1. Если известна длина всех сторон прямоугольника, просто посчитайте сумму этих величин.
2. Если вы знаете только две соседние стороны, суммируйте их и умножьте результат на два.

• P — искомый периметр;
• a, b, c, d — стороны прямоугольника.

Сейчас читают 🔥

Зная любую сторону и площадь

1. Поделите площадь на длину известной стороны.
2. Прибавьте результат к известной стороне.
3. Умножьте полученное число на два.

• P — искомый периметр прямоугольника;
• a — известная сторона;
• S — площадь прямоугольника.

Зная любую сторону и диагональ

1. Посчитайте разность квадратов диагонали и стороны.
2. Найдите корень из результата.
3. Прибавьте полученное число к известной стороне.
4. Умножьте результат на два.

• P — искомый периметр прямоугольника;
• a — известная сторона;
• d — диагональ прямоугольника.

Зная одну любую сторону и радиус описанной окружности

1. Умножьте квадрат радиуса на четыре.
2. Посчитайте разность полученного числа и квадрата известной стороны.
3. Найдите корень из результата.
4. Прибавьте полученное число к известной стороне.
5. Умножьте результат на два.

• P — искомый периметр прямоугольника;
• a — известная сторона;
• R — радиус окружности, описанной вокруг прямоугольника.

Читайте также 📐✂️📌

Периметр, площадь и объем

Данный материал содержит геометрические фигуры с измерениями. Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни. 

Периметр геометрической фигуры

Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.

Вычислим периметр следующей фигуры:

Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.

У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:

Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:

P = 9 см + 4 см + 9 см + 4 см = 26 см.

Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»

P = 2 × (9 + 4) = 18 + 8 = 26 см.

Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см»

нужно понимать как «длина каждой стороны квадрата равна 5 см»

Чтобы вычислить периметр, сложим все стороны:

P = 5 см + 5 см + 5 см + 5 см = 20 см

Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза

P = 5 см × 4 = 20 см

---

Площадь геометрической фигуры

Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.

Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.

Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.

Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.

Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:

Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.

Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:

Допустим, потребовалось измерить площадь следующей комнаты:

Определимся в каких квадратах будем измерять площадь.

В данном случае площадь удобно измерить в квадратных метрах:

Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:

Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.

---

Площадь прямоугольника

В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.

Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.

Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.

Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:

Теперь измерим ширину. Пусть она составила 3 метра:

Умножим длину (4 м) на ширину (3 м).

4 × 3 = 12

Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:

Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:

---

Площадь квадрата

Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см

Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.

Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см

3 × 3 = 9

В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:

Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 3².

Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют

возведением в квадрат.

---

Обозначения

Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу

S = a²

где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.

Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см². Это обозначение заменяет словосочетание «квадратный сантиметр».

Например, вычислим площадь квадрат со стороной 2 см.

Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:

Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м². Это обозначение заменяет словосочетание «квадратный метр».

Вычислим площадь квадрата со стороной 3 метра

Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:

Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:

S = a × b

Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см², м², км². Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.

Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см

Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:

В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).

---

Перевод единиц измерения площади

Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:

Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.

1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.

Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см

Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100

S = 100² = 10 000 см²

Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.

1 м²  = 10 000 см²

Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.

Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.

А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.

Например, переведём 100 000 см² в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см² это один квадратный метр, то сколько раз 100 000 см² будут содержать по 10 000 см²»

100 000 см² : 10 000 см² = 10 м²

Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км² в квадратные метры.

Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000

S = 1000² = 1 000 000 м²

Получается, что на один квадратный километр приходится один миллион квадратных метров:

1 км²  = 1 000 000 м²

Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.

Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.

Итак, вернёмся к нашей задаче. Требовалось перевести 2 км² в квадратные метры. Умножим 2 км² на 1 000 000

2 км² × 1 000 000 = 2 000 000 м²

А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.

Например, переведём 3 500 000 м² в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м² это один квадратный километр, то сколько раз 3 500 000 м² будут содержать по 1 000 000 м²»

3 500 000 м² : 1 000 000 м² = 3,5 км²

---

Пример 2. Выразить 7 м² в квадратных сантиметрах.

Умножим 7 м² на 10 000

7 м² = 7 м² × 10 000 = 70 000 см²

---

Пример 3. Выразить 5 м² 13 см² в квадратных сантиметрах.

5 м² 13 см² = 5 м² × 10 000 + 13 см² = 50 013 см²

---

Пример 4. Выразить 550 000 см² в квадратных метрах.

Узнаем сколько раз 550 000 см² содержит по 10 000 см². Для этого разделим 550 000 см² на 10 000 см²

550 000 см² : 10 000 см² = 55 м²

---

Пример 5. Выразить 7 км² в квадратных метрах.

Умножим 7 км² на 1 000 000

7 км² × 1 000 000 = 7 000 000 м²

---

Пример 6. Выразить 8 500 000 м² в квадратных километрах.

Узнаем сколько раз 8 500 000 м² содержит по 1 000 000 м². Для этого разделим 8 500 000 м² на 1 000 000 м²

8 500 000 м² × 1 000 000 м² = 8,5 км²

---

Единицы измерения площади земельных участков

Площади небольших земельных участков удобно измерять в квадратных метрах.

Площади более крупных земельных участков измеряются в арах и гектарах.

Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м²). В виду частого распространения такой площади (100 м²) она стала использоваться, как отдельная единица измерения.

Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м² каждый, то есть:

3 а = 100 м² × 3 = 300 м²

В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м². Примеры:

1 сотка = 100 м²

2 сотки = 200 м²

10 соток = 1000 м²

Гектар (сокращенно: га) — это площадь, равная 10 000 м². Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м² каждый, то есть:

20 га = 10 000 м² × 20 = 200 000 м²

---

Прямоугольный параллелепипед и куб

Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед:

Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.

Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:

Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:

---

Объём геометрической фигуры

Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.

Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.

Измерить объём какой-нибудь фигуры означает выяснить сколько  кубических единиц вмещается в данную фигуру.

Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:

Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:

Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см³). Тогда объём V рассмотренного нами параллелепипеда равен 12 см³

V = 12 см³

Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .

Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

V = abc

где, a — длина, b — ширина, c — высота

Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см³. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат

Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.

Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:

Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:

V = 3 × 3 × 3 = 27 см³

Действительно, в исходный куб вмещается 27 кубиков длиной 1 см

При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 3³.

V = 3³ = 27 см³

Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.

Таким образом, объём куба вычисляется по следующему правилу:

V = a³

Где a — длина куба.

---

Кубический дециметр. Кубический метр

Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м³). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм³).

Другое название одного кубического дециметра – один литр.

1 дм³ = 1 литр

---

Перевод единиц измерения объёма

Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:

Пример 1. Выразить 1 кубический метр в кубических сантиметрах.

Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.

Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см

Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:

V = 100³ = 1 000 000 см³

Получается, что на один кубический метр приходится один миллион кубических сантиметров:

1 м³  = 1 000 000 см³

Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.

Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.

А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.

Например, переведём 300 000 000 см³ в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см³ это один кубический метр, то сколько раз 300 000 000 см³ будут содержать по 1 000 000 см³»

300 000 000 см³ : 1 000 000 см³ = 300 м³

---

Пример 2. Выразить 3 м³ в кубических сантиметрах.

Умножим 3 м³ на 1 000 000

3 м³ × 1 000 000 = 3 000 000 см³

---

Пример 3. Выразить 60 000 000 см³ в кубических метрах.

Узнаем сколько раз 60 000 000 см³ содержит по 1 000 000 см³. Для этого разделим 60 000 000 см³ на 1 000 000 см³

60 000 000 см³ : 1 000 000 см³ = 60 м³

---

Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.

1 литр = 1 дм³

Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм³. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.

Пример 1. Перевести 5 литров в кубические дециметры.

Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1

5 л × 1 = 5 дм³

---

Пример 2. Перевести 6000 литров в кубические метры.

Шесть тысяч литров это шесть тысяч кубических дециметров:

6000 л × 1 = 6000 дм³

Теперь переведём эти 6000 дм³ в кубические метры.

Длина, ширина и высота одного кубического метра равны 10 дм

Если вычислить объём этого куба в дециметрах, то получим 1000 дм³

V = 10³= 1000 дм³

Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм³ содержит по 1 000 дм³

6 000 дм³ : 1 000 дм³ = 6 м³

Значит, 6000 л = 6 м³.

---

Таблица квадратов

В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.

Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.

Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.

Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.

Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576

24² = 576

---

Таблица кубов

Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.

Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.

35³ = 42875

---

Задания для самостоятельного решения

Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.

Решение

P = 2(a + b)

a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см

Ответ: периметр прямоугольника равен 16 см.

Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.

Решение

S = ab
a = 6, b = 2
S = 6 × 2 = 12 см²

Ответ: площадь равна 12 см².

Задача 3. Площадь прямоугольника составляет 12 см². Длина составляет 6 см. Найдите ширину прямоугольника.

Решение

S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2

Ответ: ширина прямоугольника составляет 2 см.

Задача 4. Вычислите площадь квадрата со стороной 8 см

Решение

S = a²
a = 8
S = 8² = 64 см²
Ответ: площадь квадрата со стороной 8 см равна 64 см²

Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.

Решение

V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см³.

Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см³

Задача 6. Объем прямоугольного параллелепипеда составляет 200 см³. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см

Решение

V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4

Ответ: высота прямоугольного параллелепипеда равна 4 см.

Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га

Решение

Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.

Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.

Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза

4 × 3 = 12 га

Ответ: пшеницей засеяно 12 га.

Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м³ его весит 740 кг.

Решение

a — длина
b — ширина
c — высота

a = 42 м
b = м
c = 42 × 0,1 = 4,2 м

Определим объем зернохранилища:

V = abc = 42 × 30 × 4,2 = 5292 м³

Определите сколько тонн зерна вмещает зернохранилище:

5292 × 740 = 3916080 кг

Переведём килограммы в тонны:

Ответ: зернохранилище вмещает 3916,08 тонн зерна.

Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.

Решение

Определим сколько литров в минуту вливается через вторую трубу:

25 л/мин × 0,75 = 18,75 л/мин

Определим сколько литров в минуту вливается в бассейн через обе трубы:

25 л/мин + 18,75 л/мин = 43,75 л/мин

Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин

43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л

1 л = 1 дм³

35 525 л = 35 525 дм³

Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:

35 525 дм³ : 1000 дм³ = 35,525 м³

Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:

V = 35,525
a = 5.8
b = 3.5
c = x

35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м

с = 1,75

Ответ: высота (глубина) бассейна составляет 1,75 м.

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Количество рулонов обоев, необходимых для оклейки комнаты

Данные для рулонов длиной 10,05 м и шириной 0,52 м.

Высота потолков, м	Периметр комнаты, м
	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
2.15 — 2.30	4	5	6	6	7	7	8	8	9	9	10	10	10	11	11	12	12	13	13	14	14	15
2.3 — 2.45	4	5	6	6	7	7	8	8	9	9	10	10	10	11	11	12	12	13	13	14	14	15
2.45 — 2.6	6	6	7	8	9	9	10	10	11	11	12	13	14	14	15	16	16	17	18	18	19	20
2.6 — 2.75	6	6	7	8	9	9	10	10	11	11	12	13	14	14	15	16	16	17	18	18	19	20
2.75 — 2.9	6	6	7	8	9	9	10	10	11	11	12	13	14	14	15	16	16	17	18	18	19	20
2.9 — 3.05	6	6	7	8	9	9	10	10	11	11	12	13	14	14	15	16	16	17	18	18	19	20
3.05 — 3.2	6	6	7	8	9	9	10	10	11	11	12	13	14	14	15	16	16	17	18	18	19	20

Данные для рулонов длиной 10,05 м и шириной 0,68 м.

Высота потолков, м	Периметр комнаты, м
	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
2.15 — 2.30	4	4	4	5	5	6	6	6	7	7	7	8	8	9	9	9	10	10	10	11	11	11
2.3 — 2.45	4	4	4	5	5	6	6	6	7	7	7	8	8	9	9	9	10	10	10	11	11	11
2.45 — 2.6	5	5	6	6	7	7	8	8	9	9	10	10	11	11	12	12	13	13	14	14	15	15
2.6 — 2.75	5	5	6	6	7	7	8	8	9	9	10	10	11	11	12	12	13	13	14	14	15	15
2.75 — 2.9	5	5	6	6	7	7	8	8	9	9	10	10	11	11	12	12	13	13	14	14	15	15
2.9 — 3.05	5	5	6	6	7	7	8	8	9	9	10	10	11	11	12	12	13	13	14	14	15	15
3.05 — 3.2	5	5	6	6	7	7	8	8	9	9	10	10	11	11	12	12	13	13	14	14	15	15

Обращаем ваше внимание, что данная информация носит справочный характер!

Как посчитать нужное количество рулонов

Чтобы рассчитать количество рулонов необходимо:

1. Во-первых, нужно рассчитать периметр помещения, не включая двери и окна. Кроме того, необходимо померить высоту стены, с учетом 10 см на каждой полосе которые нужно будет обрезать.

2. После того как мы рассчитали периметр комнаты, мы можем рассчитать какое число полос нам нужно. Чтобы сделать это, разделим периметр на ширину полосы (0.53m). Рассчитаем только целые числа. Округлим до следующего целого числа, если есть десятичный остаток.

3. Далее, возьмем длину в рулонах (10 м) и разделим на высоту (не забудьте добавить 10 см). Наконец, чтобы рассчитать количество рулонов обоев нужно взять число требуемых полос и разделить на число полос в рулоне.

Автоматический расчет количества рулонов

Как рассчитать периметр комнаты — Наука

Наука 2021

Если вас когда-либо отправили в свою комнату для наказания, вы, возможно, обошли его периметр от скуки. Периметр объекта — это измерение границ его площади. Подобно определению площади комнаты, опреде

Содержание:

Если вас когда-либо отправили в свою комнату для наказания, вы, возможно, обошли его периметр от скуки. Периметр объекта — это измерение границ его площади. Подобно определению площади комнаты, определение ее периметра требует от вас измерения длины стен; но в отличие от области, периметр касается только границ пространства.

Умножьте длину одной стены на 4, чтобы вычислить периметр квадратной комнаты, так как все четыре стороны квадрата имеют одинаковую длину по определению. Думайте о полу как о квадрате. Например, предположим, что длина одной стены составляет 20 футов. 20, умноженное на 4, дает периметр 80 футов.

Удвойте измерения ширины и длины и сложите их вместе, чтобы вычислить периметр прямоугольной комнаты. Например, предположим, что длина комнаты составляет 18 футов, а ширина — 14 футов. Удвоение 18 приводит к 36, а удвоение 14 — к 28. Сложение 36 и 28 вместе составляет 64 фута.

Суммируйте длины трех стен вместе, чтобы вычислить периметр треугольной комнаты. Например, длина стен составляет 15 футов, 20 футов и 20 футов. Сложение этих длин вместе дает периметр 55 футов.

Умножьте диаметр круглой комнаты на пи, чтобы вычислить ее периметр. Диаметр круга — это расстояние от одной стороны до другой, проходящее через центр. Pi, или π, является неповторяющейся математической константой в виде десятичной дроби, которая начинается с 3.14159. Например, предположим, что диаметр комнаты составляет 20 футов. Умножение 20 на π дает округленный периметр 62.832.

Суммируйте длины всех стен, чтобы вычислить периметр любой комнаты. Например, предположим, что в комнате есть две изогнутые стены размером 18 и 20 футов и три прямые стены размером 18, 24 и 15 футов. Добавление этих чисел приводит к периметру 95 футов.

Как узнать периметр помещения — MOREREMONTA

Как посчитать периметр комнаты

Периметр — это длина геометрической фигуры по её внешней границе.

Периметр комнаты — это сумма длин сторон комнаты. Соответственно для вычисления периметра необходимо суммировать все стороны.

Формула расчета периметра комнаты:

А — длина комнаты;
В — ширина комнаты;

Для комнаты произвольной конфигурации используются более сложные формулы расчета и этот расчет быстрее и удобнее выполнить с применением чертежных программных продуктов.

Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

В нашей проектной организации Вы можете заказать расчет периметра комнаты на основании технологического или конструкторского задания. Расчет выполним для комнаты любой конфигурации по Вашему рисунку с применением самых современных чертежных программ 2D-черчения.

На этой странице представлен самый простой онлайн калькулятор расчета периметра комнаты. С помощью этого калькулятора в один клик вы можете вычислить периметр комнаты, если известны длина и ширина.

Во время ремонта может возникнуть ситуация, когда необходимо знать точный периметр комнаты, например при покупке плинтуса или при расчете количества обоев и напольного покрытия. Сделать это просто, если помещение имеет стандартную форму. Но что делать, если нам нужно произвести расчет для коридора, который имеет множество углов, или для спальни необычной формы? В этом процессе помогут некоторые хитрости, прибегнуть к которым можно при планировании ремонта.

Расчет для стандартных помещений: квадрат и прямоугольник

Чаще всего встречаются помещения, стены которых образуют прямоугольник или квадрат. В данном случае нам понадобятся:

Для начала вспомним, что такое периметр. Это геометрическая величина, являющаяся суммой длин всех сторон фигуры. Высчитать его еще проще, чем площадь пола.

Самый простой случай – это помещение, представляющее собой квадрат, то есть все его стороны равны. Тогда измеряем одну сторону квадрата, приложив рулетку к стыку стены и пола.

Если у вас нет рулетки, используйте нитку, сделав отрезок, соответствующий расстоянию от угла до угла помещения, и измерьте его с помощью линейки.

Искомую величину можно посчитать, умножив результат измерения на 4. Так, для спальни, имеющей форму квадрата со стороной, равной 5 метрам, периметр будет равен:

Немного интереснее, когда комната является прямоугольником. Это означает, что длины противоположных стен равны между собой. В таком случае меряем расстояние от угла до угла двух смежных стен рулеткой, складываем полученные числа между собой и умножаем на 2. Для наглядности рассмотрим пример: дана гостиная прямоугольной формы, длина одной ее стены равна 5 метрам, другой – 5,5 м. Тогда периметр будет равен:

(5 + 5,5) х 2 = 21 (м)

Не забывайте, что даже при точном расчете количества стройматериалов их нужно покупать с небольшим запасом на случай порчи.

Нестандартные варианты: многоугольник и круг

Легко рассчитать периметр, когда противоположные стороны фигуры равны между собой. Усложним ситуацию: у имеющейся кухни больше четырех углов. В таком случае придется замерить каждый отрезок от одного угла до другого, после чего сложить все результаты измерений. Данный способ отличается от предыдущего тем, что для того чтобы рассчитать периметр, нужно больше исходных данных.

Возьмем кухню, имеющую форму шестиугольника с нишей. Тогда количество стен, которые нам придется измерить, сложив затем полученные значения, будет равно 8.

Усложним ситуацию еще больше: зал представляет собой окружность. Тут не поможет замер от угла до угла, так как их просто нет. Если существует уверенность, что это действительно круг, а не эллипс, то поможет знание геометрии. Периметр представляет собой длину окружности. А длина окружности, в свою очередь, является произведением диаметра окружности на число π.

Звучит страшно, но на самом деле все просто.

1. Находим центр комнаты и обозначаем его.
2. Закрепляем нитку у одной стены и проводим до противоположной через центр помещения.
3. Измеряем длину полученного отрезка. Это и есть диаметр окружности.

Теперь нужно считать. Берем полученный диаметр и умножаем на число π. Все знают, что данное число бесконечно большое. Но нам не нужна точность до сотых миллиметра, поэтому берем 3,14. Таким образом, периметр окружности является длиной отрезка от стены до стены через середину комнаты, умноженной на 3,14.

Значит, имея круглое помещение диаметром 5 метров, мы получим нужное нам значение следующим образом:

Полезные советы

Что делать, если совершенно не хочется считать или нет желания ползать по комнате, вымеряя рулеткой стены? Есть несколько полезных советов:

• Возьмите у знакомого лазерную рулетку. С этим устройством можно будет провести все замеры самостоятельно, в отличие от рулетки, при использовании которой нужен товарищ, удерживающий ее конец. Кроме того, прибор выдаст более точный результат, так как лазерный луч не будет отклоняться. Это поможет точнее рассчитать периметр комнаты.
• Используйте длинную нитку. Гораздо удобнее будет крепить части нитки к углам, не прерывая замер. Нитка должна разматываться до тех пор, пока не встретится собственным концом – началом замера. Её конечная длина – это и есть искомое значение. Такой способ поможет при наличии помещения, имеющего форму эллипса, так как по-другому рассчитать длину данной фигуры будет проблематично.

Таким образом, за небольшое время можно провести все необходимые замеры и получить готовый результат. Однако стоит помнить, что в результате нужно учитывать погрешность, чтобы не закупить стройматериала меньше, чем нужно. Например, если стена неровная, даже при точных расчетах в итоге потребуется больше плинтуса для сглаживания недочетов.

Периметр что это такое и как правильно его посчитать, к примеру периметр здания, или периметр комнаты.

По сути периметр та же длина границы дома, или границы помещения.

Но не просто длинна, а сумма, общая длина границы (внешний контур).

Например комната 5Х3, длина одной стены 5 метров, второй 3.

В сумме длин и будет периметр, то есть 5 + 5 + 3 + 3 = 16 (периметр 16 метров).

Тоже самое и с домом, периметр дома высчитывают к примеру для обустройства (изготовления) отмостки вокруг дома.

Ширина отмостки умноженная на периметр = площадь отмостки, если к этим величинам добавить толщину отмостки, то можно высчитать кубатуру.

Как правильно посчитать периметр?

Нужна рулетка, советую вот такую

Но если нет таких инструментов, подойдёт обычная, длина измерительного полотна подбирается индивидуально.

Нужен блокнот ручка, возможно калькулятор.

Если помещение большое, или если измеряем периметр дома, то лучше работать вдвоём.

Устанавливаем зацеп рулетки на края стены, далее отмеряем длину стены, записываем, затем точно так же измеряется длина всех стен и в конце находится (суммированием) общая длина, это и есть периметр.

Периметр прямоугольника — как его найти (формула)

Обновлено 18 января 2021

1. Что такое прямоугольник и что такое периметр
2. Как найти периметр прямоугольника
3. Другие формулы для расчета

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое периметр прямоугольника и по каким формулам его можно посчитать.

Тема в общем-то простая, каждый из нас изучал ее еще в начальных классах. Тем не менее с возрастом кто-то мог что-нибудь и подзабыть.

Но для начала предлагаем освежить теоретическую базу и вспомнить, что такое прямоугольник.

Что такое прямоугольник и что такое периметр

Прямоугольник – это геометрическая фигура, которая представляет собой четырехугольник, а конкретно параллелограмм (фигура, у которой противоположные стороны равны и параллельны). Но параллелограмм не обычный, а с особенностями. У него все стороны пересекаются друг с другом под прямым углом.

Выглядит прямоугольник соответственно:

А частным случаем прямоугольника является квадрат:

У такого прямоугольника стороны не только пересекаются под прямым углом, но и равны между собой.

Как и многие термины в математике, слово «периметр» пришло к нам из Древней Греции. Дословно оно означает «περιμετρέο» — «окружность» или «измерять вокруг». Таким образом,

Периметр – это совокупная длина границ любой геометрической фигуры. Этим словом обозначают как сами границы, так и их математическое значение.

С этим словом мы часто встречаемся в повседневной жизни. Например, когда нужно поставить забор на дачном участке, то его устанавливают по периметру участка. И мы понимаем, что речь идет о границах.

Также, солдаты или полицейские часто стоят в оцеплении «по периметру» какой-то территории. А кулинары часто украшают торт фруктами или кремовыми цветами также «по периметру».

Как найти периметр прямоугольника

Возьмем для примера такой прямоугольник:

Исходя из общего определения, чтобы посчитать периметр прямоугольника, надо просто сложить все его стороны.

Периметр в математике обозначается латинской буквой «Р». И соответственно формула выглядит так:

С учетом равенства сторон, формулы можно существенно упростить:

или

Предположим, что у нас длина прямоугольника равна 4 сантиметрам, а ширина 2. Тогда периметр этой геометрической фигуры составит:

И тут появляется важное замечание. Периметр измеряется в тех же величинах, что и длины сторон прямоугольника. Это могут быть миллиметры, сантиметры, метры, километры и так далее.

В случае с квадратом, который, напомним, является частным случаем прямоугольника, посчитать периметр еще проще. Благодаря тому, что у него все стороны равны (назовем их условно «а»), формула выглядит так:

или

Опять же приведем конкретный пример. Если возьмем квадрат со стороной 4 сантиметра, то его периметр составит P = 4 * 4 = 16 сантиметров.

Другие формулы для расчета периметра прямоугольника

Иногда школьникам предлагают такую задачу – нужно вычислить периметр прямоугольника, зная его площадь и длину одной стороны.

Тут надо знать, как вычисляется сама площадь. Для этого надо просто перемножить длины двух сторон:

Соответственно, мы можем определить длину недостающей нам стороны. Для этого надо просто разделить площадь на другую сторону:

Таким образом, мы у нас будут значения обеих сторон прямоугольника. А уже после периметр вычисляется по стандартной формуле.

Бывают и более сложные задачи по нахождению периметра прямоугольники, например, как в приведенном ниже видео:

Вместо заключения

Зная длины сторон, можно вычислять и периметры более сложных прямоугольных фигур. Вот таких:

Страшно выглядят они только на первый взгляд. А на деле, надо просто провести недостающую линию и разделить каждую из фигур на два прямоугольника. Далее вычисляем их периметры по отдельности и складываем друг с другом. Как результат – общий периметр фигуры.

Вот и все, что мы хотели сегодня рассказать.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Как найти периметр прямоугольника

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Расчетная область | SkillsYouNeed

Площадь — это мера того, сколько места внутри фигуры. Расчет площади формы или поверхности может быть полезен в повседневной жизни — например, вам может потребоваться знать, сколько краски нужно купить, чтобы покрыть стену, или сколько семян травы вам нужно, чтобы засеять лужайку.

На этой странице описаны основные сведения, которые необходимо знать для понимания и расчета площадей общих форм, включая квадраты и прямоугольники, треугольники и круги.

Расчет площади сеточным методом

Когда фигура рисуется на масштабированной сетке, вы можете найти площадь, подсчитав количество квадратов сетки внутри фигуры.

В этом примере внутри прямоугольника 10 квадратов сетки.

---

Чтобы найти значение площади с использованием метода сетки, нам нужно знать размер, который представляет квадрат сетки.

В этом примере используются сантиметры, но тот же метод применяется к любой единице длины или расстояния. Например, вы можете использовать дюймы, метры, мили, футы и т. Д.

В этом примере каждый квадрат сетки имеет ширину 1 см и высоту 1 см. Другими словами, каждый квадрат сетки равен одному квадратному сантиметру.

Подсчитайте квадраты сетки внутри большого квадрата, чтобы найти его площадь.

Есть 16 маленьких квадратов, поэтому площадь большого квадрата составляет 16 квадратных сантиметров.

В математике мы сокращаем «квадратные сантиметры» до ² . ² означает «в квадрате».

Каждый квадрат сетки равен 1 см ² .

Площадь большого квадрата 16см ² .

---

Подсчет квадратов на сетке для определения площади работает для всех форм — если известны размеры сетки. Однако этот метод становится более сложным, когда фигуры не точно соответствуют сетке или когда вам нужно подсчитать доли квадратов сетки.

В этом примере квадрат не точно помещается на сетке.

Мы все еще можем вычислить площадь, считая квадраты сетки.

• Имеется 25 квадратов полной сетки (заштрихованы синим цветом).
• 10 квадратов полусетки (заштрихованы желтым цветом) — 10 полуквадратов равны 5 полным квадратам.
• Также есть 1 четверть квадрата (заштрихована зеленым) — (или 0,25 целого квадрата).
• Сложите целые квадраты и дроби вместе: 25 + 5 + 0.25 = 30,25.

Следовательно, площадь этого квадрата составляет 30,25 см ² .

Вы также можете записать это как 30¼см ² .

---

Хотя использование сетки и подсчет квадратов внутри фигуры — очень простой способ изучения концепций площади, он менее полезен для нахождения точных областей с более сложными формами, когда можно сложить много частей квадратов сетки.

Площадь можно рассчитать с помощью простых формул, в зависимости от типа фигуры, с которой вы работаете.

Остальная часть этой страницы объясняет и дает примеры того, как вычислить площадь фигуры без использования системы сеток.

---

Площади простых четырехугольников:

квадратов, прямоугольников и параллелограммов

Простейшие (и наиболее часто используемые) вычисления площади выполняются для квадратов и прямоугольников.

Чтобы найти площадь прямоугольника, умножьте его высоту на ширину.

Для квадрата вам нужно только найти длину одной из сторон (поскольку каждая сторона имеет одинаковую длину), а затем умножить это на себя, чтобы найти площадь.Это то же самое, что сказать длину ² или длину в квадрате.

Хорошей практикой является проверка того, что фигура на самом деле является квадратом, путем измерения двух сторон. Например, стена в комнате может выглядеть как квадрат, но когда вы ее измеряете, вы обнаруживаете, что на самом деле это прямоугольник.

Часто в реальной жизни формы могут быть более сложными. Например, представьте, что вы хотите найти площадь пола, чтобы заказать нужное количество ковра.

Типовой план помещения не может состоять из простого прямоугольника или квадрата:

В этом и других подобных примерах фокус состоит в том, чтобы разделить фигуру на несколько прямоугольников (или квадратов).Неважно, как вы разделите фигуру — любое из трех решений даст один и тот же ответ.

Для решений 1 и 2 необходимо создать две фигуры и сложить их площади, чтобы найти общую площадь.

Для решения 3 вы создаете большую форму (A) и вычитаете из нее меньшую форму (B), чтобы найти площадь.

---

Другая распространенная проблема — найти область границы — фигуры внутри другой фигуры.

В этом примере показана дорожка вокруг поля — ширина дорожки 2 метра.

Опять же, в этом примере есть несколько способов определить площадь пути.

Вы можете просмотреть путь как четыре отдельных прямоугольника, вычислить их размеры, а затем их площадь и, наконец, сложить области, чтобы получить итог.

Более быстрый способ — вычислить площадь всей формы и площадь внутреннего прямоугольника. Вычтите внутреннюю площадь прямоугольника из всей, оставив площадь пути.

• Площадь всей формы составляет 16 м × 10 м = 160 м ² .
• Мы можем определить размеры средней секции, потому что знаем, что путь по краю имеет ширину 2 метра.
• Ширина всей формы составляет 16 м, а ширина пути по всей форме — 4 м (2 м слева от формы и 2 м справа). 16 м — 4 м = 12 м
• То же самое для высоты: 10м — 2м — 2м = 6м
• Итак, мы подсчитали, что средний прямоугольник имеет размер 12 × 6 м.
• Таким образом, площадь среднего прямоугольника составляет: 12 м × 6 м = 72 м ² .
• Наконец, мы убираем область среднего прямоугольника из области всей формы. 160 — 72 = 88м ² .

Площадь тропы 88м ² .

---

Параллелограмм — это четырехсторонняя форма с двумя парами сторон равной длины — по определению прямоугольник — это разновидность параллелограмма. Однако большинство людей склонны думать о параллелограммах как о четырехсторонних фигурах с наклонными линиями, как показано здесь.

Площадь параллелограмма рассчитывается так же, как и для прямоугольника (высота × ширина), но важно понимать, что высота означает не длину вертикальных (или отклоненных от вертикали) сторон, а расстояние между сторонами.

Из диаграммы вы можете видеть, что высота — это расстояние между верхней и нижней сторонами фигуры, а не длина стороны.

Представьте себе воображаемую линию под прямым углом между верхней и нижней сторонами. Это высота.

---

Области треугольников

Может быть полезно думать о треугольнике как о половине квадрата или параллелограмма.

Предполагая, что вы знаете (или можете измерить) размеры треугольника, вы можете быстро вычислить его площадь.

Площадь треугольника (высота × ширина) ÷ 2.

Другими словами, вы можете вычислить площадь треугольника так же, как площадь квадрата или параллелограмма, а затем просто разделите свой ответ на 2.

Высота треугольника измеряется по прямой линии от нижней линии (основания) до «вершины» (верхней точки) треугольника.

Вот несколько примеров:

Площадь трех треугольников на диаграмме выше одинакова.

Каждый треугольник имеет ширину и высоту 3 см.

Площадь рассчитана:

(высота × ширина) ÷ 2

3 × 3 = 9

9 ÷ 2 = 4,5

Площадь каждого треугольника составляет 4,5 см ² .

---

В реальных ситуациях вы можете столкнуться с проблемой, требующей найти площадь треугольника, например:

Вы хотите покрасить фронтальный конец сарая. Вам нужно посетить магазин украшений только один раз, чтобы получить нужное количество краски.Вы знаете, что литр краски покроет 10 м ² стены. Сколько краски нужно, чтобы покрыть фронтон?

Вам нужно три измерения:

A — Общая высота до вершины крыши.

B — Высота вертикальных стен.

C — Ширина здания.

В этом примере измерения:

A — 12,4 м

B — 6,6 м

C — 11,6 м

Следующий этап требует дополнительных расчетов.Подумайте о здании как о двух формах: прямоугольнике и треугольнике. По имеющимся у вас измерениям вы можете рассчитать дополнительное измерение, необходимое для определения площади фронтона.

Размер D = 12,4 — 6,6

D = 5,8 м

Теперь вы можете определить площадь двух частей стены:

Площадь прямоугольной части стены: 6,6 × 11,6 = 76,56 м ²

Площадь треугольной части стены: (5.8 × 11,6) ÷ 2 = 33,64 м ²

Сложите эти две области вместе, чтобы получить общую площадь:

76,56 + 33,64 = 110,2 м ²

Как вы знаете, один литр краски покрывает 10 м ² стены, поэтому мы можем рассчитать, сколько литров нам нужно купить:

110,2 ÷ 10 = 11,02 л.

На самом деле вы можете обнаружить, что краска продается только в 5-литровых или 1-литровых канистрах, результат — чуть более 11 литров. У вас может возникнуть соблазн округлить до 11 литров, но, если мы не будем разбавлять краску водой, этого будет недостаточно.Таким образом, вы, вероятно, округлите до следующего целого литра и купите две 5-литровые банки и две 1-литровые банки, что в сумме составит 12 литров краски. Это позволит избежать любых потерь и оставит большую часть литра для подкраски позднее. И не забывайте, что если вам нужно нанести более одного слоя краски, вы должны умножить количество краски для одного слоя на количество необходимых слоев!

---

Области кругов

Чтобы вычислить площадь круга, вам необходимо знать его диаметр или радиус .

Диаметр круга — это длина прямой линии от одной стороны круга до другой, проходящей через центральную точку круга. Диаметр в два раза больше длины радиуса (диаметр = радиус × 2)

Радиус круга — это длина прямой линии от центральной точки круга до его края. Радиус составляет половину диаметра. (радиус = диаметр ÷ 2)

Вы можете измерить диаметр или радиус в любой точке окружности — важно измерять, используя прямую линию, проходящую через (диаметр) или заканчивающуюся в (радиусе) центром окружности.

На практике при измерении окружностей часто легче измерить диаметр, а затем разделить на 2, чтобы найти радиус.

Радиус нужен для вычисления площади круга, формула:

площадь круга = πR ² .

Это означает:

π = Pi — постоянная, равная 3,142.

R = радиус окружности.

R ² (радиус в квадрате) означает радиус × радиус.

---

Следовательно, круг с радиусом 5 см имеет площадь:

3.142 × 5 × 5 = 78,55 см ² .

Круг диаметром 3 м имеет площадь:

Сначала прорабатываем радиус (3м ÷ 2 = 1,5м)

Затем примените формулу:

πR ²

3,142 × 1,5 × 1,5 = 7,0695.

Площадь круга диаметром 3 м составляет 7,0695 м ² .

---

Заключительный пример

В этом примере используется большая часть содержимого этой страницы для решения простых задач с областями.

Это дом Рубена М. Бенджамина в Блумингтоне, штат Иллинойс, внесенный в Национальный реестр исторических мест США (номер записи: 376599).

Этот пример включает поиск передней части дома, деревянной решетчатой ​​части — исключая дверь и окна. Вам нужны следующие размеры:

A — 9,7 м	B — 7,6 м
C — 8,8 м	D — 4,5 м
E — 2.3 мес	F — 2,7 м
G — 1,2 м	H — 1,0 м

Примечания:

• Все размеры являются приблизительными.
• Не стоит беспокоиться о границе вокруг дома — она ​​не учтена в измерениях.
• Мы предполагаем, что все прямоугольные окна одинакового размера.
• Размер круглого окна — это диаметр окна.
• Размер двери включает ступеньки.

Какова площадь деревянной реечной части дома?

Работы и ответы ниже:

---

---

Ответы на приведенный выше пример

Сначала определите площадь основной формы дома — прямоугольника и треугольника, составляющих форму.

Главный прямоугольник (B × C) 7,6 × 8,8 = 66,88 м ² .

Высота треугольника (A — B) 9,7 — 7,6 = 2,1.

Следовательно, площадь треугольника равна (2.1 × C) ÷ 2.
2,1 × 8,8 = 18,48. 18,48 ÷ 2 = 9,24 м ² .

Общая площадь фасада дома равна сумме площадей прямоугольника и треугольника:

66,88 + 9,24 = 76,12 м ² .

Затем проработайте площади окон и дверей, чтобы их можно было вычесть из всей площади.

Площадь двери и ступеней составляет (Д × В) 4,5 × 2,3 = 10,35 м ² .

Площадь одного прямоугольного окна составляет (G × F) 1.2 × 2,7 = 3,24 м ² .

Есть пять прямоугольных окон. Умножьте площадь одного окна на 5.

3,24 × 5 = 16,2 м2. (общая площадь прямоугольных окон).

Круглое окно имеет диаметр 1 м, поэтому радиус 0,5 м.

Используя πR ² , определите площадь круглого окна: 3,142 × 0,5 × 0,5 =. 0,7855м ² .

Затем сложите площади двери и окон.

(зона двери) 10,35 + (прямоугольная зона окон) 16.2 + (площадь круглого окна) 0,7855 = 27,3355

Наконец, вычтите общую площадь окон и дверей из всей площади.

76,12 — 27,3355 = 48,7845

Площадь деревянного реечного фасада дома и ответ на проблему: 48,7845м ² .

Вы можете округлить ответ до 48,8 м ² или 49 м ² .

См. Нашу страницу Оценка, приближение и округление .

Калькулятор обрезки и формования — Дюймовый калькулятор

Оцените количество опор основания, дверной коробки, оконной рамы, короны и перил стульев, необходимых для завершения комнаты, указав длину и ширину вашей комнаты.При желании введите количество окон и дверей, чтобы оценить необходимое количество кожухов.

Как оценить количество необходимой обрезки

Установка отделки способна улучшить вид любого помещения. Чтобы оценить количество декоративных молдингов, необходимых для завершения комнаты, необходимо определить периметр помещения в футах.

Расчет основания, перил стула и молдингов короны

Основание, поручень стула и карнизы короны можно рассчитать одним и тем же методом.Сначала измерьте длину и ширину комнаты в футах. Используйте наши инструменты для преобразования единиц длины, чтобы преобразовать измерения длины в футы.

Следующим шагом будет определение периметра комнаты. Умножьте длину на 2 и ширину на 2, затем сложите значения, например. (длина × 2) + (ширина × 2) = периметр. Вычтите длину дверей или окон, разделяющих комнату. Например, если у вас есть входная дверь размером 36 дюймов в комнату, вычтите 3 фута из измерения периметра.

Молдинги продаются с линейной опорой или длиной 8 футов.Если выбранный вами плинтус продается с линейной опорой, вы должны получить количество опор, необходимое для вашего периметра. Подробнее о расчете линейных метраж. Если ваша лепнина продается в виде 8-дюймовых деталей, вам нужно найти количество деталей, необходимое для завершения вашего проекта. Для этого разделите размер периметра на 8 и округлите в большую сторону, например. (периметр / 8).

Поскольку стыки в обрезке нежелательны, возможно, стоит приобрести небольшую дополнительную обрезку, чтобы учесть порезы и отходы материала, чтобы при необходимости можно было использовать более длинные детали.Это суждение, которое вам нужно будет сделать в зависимости от вашей комнаты.

Расчет дверной и оконной опалубки

Расчет необходимого количества оконной рамы аналогичен расчету молдингов основания. Начните с измерения периметра двери или окна и преобразования его в футы.

Учтите, что наличник выходит за край двери или окна на толщину обшивки. Учет этого, прибавляя толщину обшивки, умноженную на 2, к каждой длине двери или окна.

Например, , если вы устанавливаете молдинг толщиной 3 дюйма на окно размером 36 x 48 дюймов, используйте следующее уравнение, чтобы определить, сколько нужно обрезки:

линейный фут = ((ширина + (толщина × 2)) × 2) + ((высота + (толщина × 2)) × 2)
линейных футов = ((36 ″ + (3 ″ × 2)) × 2) + ((48 ″ + (3 ″ × 2)) × 2)
линейных футов = ((36 ″ + 6 ″) × 2) + ((48 ″ + 6 ″) × 2)
линейных футов = (42 ″ × 2) + (54 ″ × 2)
линейных футов = 84 ″ + 108 ″
линейных футов = 192 ″ = 16 ′

Технически это окно может быть выполнено с использованием двух 8-дюймовых профилей, но, скорее всего, потребуются три 8-дюймовых элемента для размещения обрезков и использования полных секций для каждой кромки.Как и в случае с основной лепниной, учтите, что следует использовать более длинные отрезки, чтобы избежать стыков, когда это возможно, что может потребовать покупки дополнительного материала.

Сколько стоит обрезка?

Для оценки стоимости необходимо умножить цену обрезки за фут на необходимую длину обрезки. Если обрезки продаются длиной 8 футов, умножьте стоимость доски на количество необходимых досок. Обрезка может варьироваться в цене от $ 0,25 до 10 $ за погонный фут в зависимости от породы дерева, толщины и сложности лепнины.

Узнайте, сколько будет стоить ваш проект отделки, с помощью профессиональных предложений плотников в вашем районе. При оценке стоимости обязательно учитывайте отходы материалов и покраску или отделку. Большую часть отделки потребуется покрасить или окрасить морилкой, что может увеличить стоимость проекта.

Как измерить комнату для плитки и рассчитать квадратные метры

Ищете профессиональные советы о том, как измерить комнату под плитку перед установкой? Вы пришли в нужное место! Для всех наших мастеров по установке плитки своими руками — не бойтесь! Наша команда экспертов готова упростить процесс измерения и расчета площади вашей плитки!

Определить, сколько плитки вам понадобится для вашего проекта, может быть сложно (особенно для поклонников улучшения дома).Независимо от того, перекрашиваете ли вы стены или пол, большое или маленькое пространство, важно иметь под рукой достаточно плитки, прежде чем приступить к укладке плитки. Последнее, что вам нужно сделать, — это осознать, что на этапе работы с плиткой вы не заказали достаточно! Точные измерения — лучший способ гарантировать, что ваша работа будет завершена вовремя, и вы получите плитки из одной партии, чтобы гарантировать максимальное соответствие.

Не волнуйтесь, мы расскажем, как рассчитать размеры этой красиво облицованной пороховой комнаты, демонстрируя нашу полированную стеклянную плитку Glacier Grey 8X16!

Правильное измерение — это, безусловно, лучший способ сэкономить время и деньги при облицовке комнаты плиткой! Эту часть проекта легко переоценить, но на самом деле она довольно проста.Выполнив несколько расчетов и немного посоветовавшись, вы можете легко получить нужные размеры для нужной плитки — не волнуйтесь, математическое образование не требуется!

Итак, как вы рассчитаете количество плиток, необходимых для вашего участка, или подтвердите свою площадь в квадратных футах? Это проще, чем ты думаешь. Просто выполните 5-шаговый процесс, описанный ниже, и прочтите наши советы, чтобы измерять как профессионал!

5 шагов для измерения площади укладки плитки

Шаг 1 — Соберите свои измерительные материалы

Ваш список поставок довольно прост, независимо от того, собираетесь ли вы купить керамическую плитку для пола для своей ванной комнаты или мраморную кухонную плиту.Вам понадобится:

* Рулетка

* Блокнот и карандаш или ручка

* Калькулятор

Независимо от того, покрываете ли вы пол в прихожей или на стенах кухни, шаги по определению необходимого количества плитки одинаковы, независимо от поверхности. Если у вас есть готовые материалы, приступим!

Шаг 2 — Измерение площади

Сначала вы должны начать с точных измерений площади, которую вы планируете выложить плиткой:

— Для квадратных или прямоугольных областей измеряет длину и ширину пространства в дюймах (квадратная область, очевидно, будет иметь одинаковую длину и ширину).

— Для круглых областей протяните рулетку через центр круга. Рулетка должна начинаться у одной стены и проходить через центр области, пока вы не дойдете до другой стороны. Эта общая длина, проходящая через центр вашего круга, называется диаметром. Половина диаметра пространства от центра до каждой стены называется радиусом , — это число, которое вам понадобится в ваших расчетах. (помните, в средней школе вы думали, что никогда не будете выполнять домашнее задание по геометрии? Теперь у вас есть шанс!)

Советы профессионалов:

* Перед тем, как снимать мерки, убедитесь, что пространство чистое и ничто не мешает провести чистую линию на рулетке.Переместите всю мебель в центр и прогоняйте всех домашних животных, которые могут встать у вас на пути! Если вы не можете очистить всю область, убедитесь, что вы можете провести рулетку по прямой линии, не сгибая и не перегибая ее над объектом.

* Если вы планируете измерить стену, снимите все картины или настенные покрытия, которые могут мешать.

Шаг 3 — Расчет покрытия

Чтобы рассчитать, сколько плитки вам нужно для комнаты, вам нужно найти общую площадь пространства, которое вы только что измерили.Это даст вам покрытие (общая площадь в квадратных футах в дюймах) для каждого пространства, которое вы планируете выложить плиткой.

-Для квадратных или прямоугольных областей умножьте , длину на ширину , а затем разделите результат на 144 , чтобы получить общую сумму в квадратных футах.

Вот пример:

Допустим, у нас есть прямоугольная комната размером 8 футов 5 дюймов x 5 футов 3

Сначала преобразуйте ширину и длину в дюймы: 101 дюйм x 63 дюйм

Затем умножьте длину на ширину: 101 дюйм x 63 дюйма = 6363 дюйм

Наконец, разделите полученную сумму на 144, чтобы найти общую площадь покрытия в квадратных футах: 6363/144 (1 квадратный фут) = 44.19 sf покрытие

Еще проще, когда у вас квадратная комната, скажем 12 футов x 12 футов

Просто умножьте 12 на 12, чтобы найти общую площадь покрытия в квадратных футах, что составляет 144 квадратных фута

— Для круглых областей разделите общую длину, измеренную в дюймах, на 2, чтобы найти радиус. Округление до ближайшего целого числа упростит расчеты. Затем умножьте радиус на пи — или 3.14. Снова округлите его до ближайшего десятичного знака, чтобы получить сумму в квадратных футах.

Вот пример:

Допустим, есть круглая область, которую вы собираетесь выложить плиткой, диаметром 20 футов

Преобразуйте размер в дюймы: 20 футов = 240 дюймов

Разделите диаметр на 2, чтобы найти радиус: 240 дюймов / 2 = 120 дюймов

Умножьте радиус на 3,14, чтобы найти общую площадь покрытия в квадратных футах: 120 дюймов * 3.14 = 376,8 кв. Футов

Округлить до ближайшего десятичного числа: Площадь покрытия 377 кв. Футов

Pro Совет:

* Если вы рассчитываете, сколько площади вам нужно покрыть настенной плиткой, вам нужно будет учесть все двери и окна. В этом случае рассчитайте покрытие для всей стены, а также квадратные метры всех дверей и окон (измеряя от верхнего края рамы, чтобы обеспечить пространство).Затем вычтите площадь всех окон и дверей из общего покрытия стены.

Шаг 4 — Рассчитайте необходимое количество плиток

Помимо общей площади в квадратных футах, вы также можете узнать приблизительное количество плиток для покрытия площади. Преобразовать площадь покрытия в количество плиток очень просто!

Сначала найдите площадь одной плитки в дюймах. (Мы перечисляем отснятый материал, который будет покрывать каждый лист или отдельная плитка в описании продукта).В случае, если вам нужно рассчитать для себя, вы можете умножить длину и ширину плитки в дюймах, чтобы определить ее площадь.

Наконец, разделите площадь пространства, рассчитанного на шаге 3, на площадь одной плитки.

Именно столько плитки нужно на пространство!

Поясним на примере:

У вас есть плитки размером 11,8 «x 11,8», и вы хотите покрыть площадь фартука шириной 48 дюймов и высотой 24 дюйма

Сначала найдите общую площадь каждой плитки: 11.8 дюймов на 11,8 дюймов = 140 дюймов (с округлением в большую сторону)

Во-вторых, найдите площадь вашего фартука: 48 x 24 дюйма = 1152 квадратных дюйма

Наконец, разделите площадь на площадь одной плитки: 1,152/140 = 8,22 необходимо плитки

Если у вас квадратная плитка, у нас есть список, который упростит вам задачу! Просто выберите размер плитки из списка и используйте приведенное ниже уравнение, чтобы определить минимальное количество плиток, которое вам нужно купить.Убедитесь, что ваша общая площадь указана в квадратных дюймах!

• 4-дюймовые плитки: Общая площадь ÷ 0,1089 = Количество необходимых 4-дюймовых плиток
• 6-дюймовых плиток: общая площадь ÷ 0,25 = необходимое количество плиток 6 дюймов
• 9-дюймовых плиток: общая площадь ÷ 0,5625 = необходимое количество 9-дюймовых плиток
• 12-дюймовые плитки: Общая площадь = необходимое количество плиток 12 дюймов
• 15-дюймовых плиток: общая площадь ÷ 1,5625 = необходимое количество плиток 15 дюймов
• 18-дюймовых плиток: общая площадь ÷ 2,25 = необходимое количество 18-дюймовых плиток

Если математика не для вас, мы предлагаем удобный калькулятор плитки для каждого дизайна, чтобы вы могли ввести общую площадь в квадратных футах с шага 3 и рассчитать необходимое количество плиток независимо от размера!

Вуаля! Просто введите площадь в квадратных футах, и мы покажем вам, сколько листов необходимо для обеспечения покрытия, а также рассчитаем цену — это продемонстрировано с нашей прекрасной стеклянной мозаичной плиткой Stardust Blue 2×8 , которая поставляется в листах по 11 листов.8 дюймов x 11,8 дюйма

Шаг 5 — Добавление излишка

Последний шаг и один из самых важных — это заказать дополнительные плитки, чтобы гарантировать полное покрытие, так как вы должны учитывать порезы, отходы и потенциальную поломку при обрезке плитки по размеру.

Чтобы точно оценить ваши потребности в избытке, важно продумать, как вы собираетесь укладывать плитку. Для большинства стандартных установок — например, стены или фартука — любые отходы должны составлять 10% от расчетной суммы.

Для более сложных узоров — скажем, вы укладываете плитку под углом 45 градусов или создаете узор типа «елочка», требующий большего количества надрезов, — мы предлагаем увеличить излишек как минимум до 15%.

15% также является идеальным излишком для плитки, которая будет укладываться в комнате с большим количеством краев и углов. Обрезка большего количества плиток для плотного прилегания по углам означает, что ожидается больше отходов.

Плитка большого формата может быть более склонна к поломке перед установкой, поэтому 30% — это идеальный избыток при заказе таких материалов, как крупноформатный керамогранит.

Как только вы определите свой идеальный процент перерасхода, рассчитайте окончательное количество, умножив площадь в квадратных футах на процент перерасхода и прибавив разницу к вашим общим квадратным футам.

Общее правило: чем больше плитка и сложнее узор, тем больше у вас отходов! Иметь лишнюю плитку — это всегда хорошо!

Готовы подсчитать, сколько плитки и отделки вам понадобится, чтобы создать эту красивую нишу для душа, не нарушая узор на нашей плитке Herringbone Pearl White Thassos Shell Tile ?

Pro Совет:

* Допустим, вы рискнули, заказав дополнительные плитки, и в итоге остались некоторые остатки.Не выбрасывайте их! Хорошая идея — держать под рукой дополнительные плитки на случай, если вам понадобится заменить их в будущем.

Если у вас много лишнего и негде его хранить, ознакомьтесь с креативными проектами декора своими руками , которые вы можете сделать из остатков плитки!

Хорошо, вы сняли размеры плитки и рассчитали излишек — не так сложно, как вы думали, верно? Прежде чем вы отправитесь заказывать идеальную плитку с помощью экспертных расчетов, у нас есть еще несколько полезных советов и способов измерения плитки, основанные на вопросах, которые нам регулярно задают! Вот несколько дополнительных советов, которые помогут вам измерять как профессионал!

Что делать, если пространство не представляет собой простой прямоугольник или квадрат?

Очень распространенная проблема — это незнание, как измерить пол в комнате необычной формы.В этом случае все, что вам нужно сделать, это измерить каждую секцию отдельно для точных расчетов.

Сначала нарисуйте на листе бумаги план этажа неправильной формы, затем разделите комнату на квадраты или прямоугольники.

Допустим, вы имеете дело с L-образной областью. Разбейте его на более мелкие части квадратов или прямоугольников и пометьте каждый из них буквой. Продолжайте измерять ширину и высоту каждой секции, а затем вычислять площадь для них как отдельные единицы, как описано в шаге 3.Наконец, сложите их вместе, чтобы получить общую площадь в квадратных футах. Чем больше отдельных пространств вы собираетесь сложить, тем больше излишков вы хотите добавить, чтобы обеспечить полное покрытие.

Расчет пола подъезда L-образной формы с нашим марокканским рисунком звезды и креста в синем и белом цвете

Например:

Вы имеете дело с L-образным полом, который можно разделить на два прямоугольника.

Размер каждого предмета 72 на 36 дюймов

Найдите площадь каждого прямоугольного сечения: 72 x 36 дюймов = 2592 квадратных дюйма

Разделите на 144, чтобы найти общую площадь покрытия в квадратных футах: 2592/144 = 18 квадратных футов на каждый кусок

Общее покрытие L-образных этажей будет 18 x 2 = Площадь покрытия 36 кв. Футов

Добавьте примерно 15% избытка: 0.15 x 36 кв. Футов = 5,4 кв. Футов

Добавьте их для окончательного расчета: 5,4 кв. Фута + 36 кв. Футов = Площадь покрытия 41,4 кв. Фута

Не забудьте добавить любые планки или плинтусы, которые вы планируете выложить плиткой!

Как измерить обрезки плитки

Для большинства вертикальных применений требуются обрезные детали с готовыми краями, требующие линейного измерения. Если вы не уверены, нужна ли вам обрезка, ознакомьтесь с одной из наших последних статей, в которой мы рассказали об обрезке плитки и их наиболее распространенном использовании .

В отличие от плитки, которая продается листом или коробкой, элементы отделки и декоративные элементы обычно продаются поштучно. Чтобы рассчитать необходимое количество, сначала найдите длину каждой обрезной детали в дюймах (например, 6-дюймовая длинная головка с выпуклым носом или 8-дюймовый карандаш). Затем измерьте длину (в дюймах) любого края, который вы собираетесь использовать для обрезки. Затем разделите длину края на длину одной обрезки плитки.

Линейные дюймы кромки / длина каждой обрезки = количество необходимых обрезков

Не забудьте добавить излишек к количеству обрезков! Мы рекомендуем начинать с не менее 10% избытка и всегда округлять до ближайшего целого фута — аналогично тому, что вы делаете с плиткой!

Например:

У вас есть 12-футовая открытая кромка, для которой требуется выпуклая ниппель, и каждая выпуклая ниппель имеет размер 6 дюймов.

Разделите длину кромки на длину выступа с выпуклой головкой: 120 дюймов / 6 дюймов = Требуется 20 головок с выпуклой головкой.

Советы по окончательному измерению в определенных областях

Хотя основной метод измерения помещения для укладки плитки является довольно универсальным, есть несколько вещей, на которые следует обратить внимание, когда дело доходит до укладки плитки для кухни и ванной комнаты. Прежде чем закончить руководство, мы рассмотрим эти советы!

— Измерение размера душа — Души можно разделить на прямоугольные секции (что является несложной частью), но если у вас есть ниша или скамейка, вам нужно будет отслеживать несколько дополнительных измерений.Разделите каждую секцию плитками, которые вы планируете использовать, сгруппируйте по материалам, чтобы рассчитать площадь в квадратных футах, необходимую для всех поверхностей. Не забудьте также указать глубину сторон ниш и окон! Если вы планируете использовать бордюрные плитки, рассчитайте их так же, как вы измерили для обрезки выше, измерив периметр душевой зоны и разделив число на 12, чтобы определить общие погонные футы бордюров, необходимых для вашего дизайна!

— Измерение пола в ванной комнате — Измерение пола в ванной комнате определенно проще, чем измерение душа, но следует учитывать дополнительные факторы.Водостоки, умывальники, туалеты или любые другие предметы, занимающие место на полу, должны учитываться при ваших измерениях при облицовке полов в ванной плиткой. Мы всегда рекомендуем облицовывать эти предметы плиткой для будущих обновлений ванной комнаты!

— Измерение кухонного пола — Для кухонь со шкафами всегда сначала измеряйте всю комнату, а затем вычтите площадь шкафа. Однако, как и полы в ванных комнатах, мы всегда рекомендуем рассчитывать квадратные метры для всего пространства, в том числе и под шкафами.

— Измерение кухонного фартука — Кухонные стены обычно имеют прямоугольную форму, но часто следует учитывать окна, двери, бытовую технику и вытяжки. Сначала вычислите площадь всей стены, которую вы планируете покрыть, а затем вычтите площадь окна или других элементов на стене. Это проще, если вы разделите пространство на более мелкие части — например, слева от диапазона, справа от диапазона и т. Д.

Подсчитать, сколько плитки вам понадобится для кухонного фартука, не так сложно, как вы думаете! Посмотрите, как мы разбили пространство на кухонной стене вокруг шкафов, столешниц и техники, чтобы выложить плитку на эту плиту Skinny Chevron Calacatta Gold Mosaic Tile !

Последние советы!

Отмерь дважды, закажи один раз! Мы надеемся, что это руководство предоставило вам некоторую полезную информацию о том, как точно измерить и рассчитать для вашего проекта плитки, и как избежать наиболее распространенных ошибок.Независимо от того, являетесь ли вы начинающим установщиком плитки своими руками или опытным, помните эти советы и рекомендации, чтобы стать профессионалом в области измерений! Если вам все еще нужна помощь в измерении или разработке решений, просто дайте нам знать. Мы всегда готовы помочь!

Сколько краски мне нужно? | Расчет количества краски

Хотите покрасить комнату в своем доме, но не знаете, сколько краски купить? Узнайте , сколько краски вам нужно , используя наше руководство.

Оцените размер вашей комнаты и потребности в краске, прежде чем идти в магазин красок.Если пользовательский цвет закончится на полпути к работе, это может означать катастрофу!

Роспись стен

Следуйте приведенным ниже инструкциям, чтобы рассчитать необходимое количество краски. Чтобы помочь, мы добавили пример: комната размером 10 x 15 футов с потолком 8 футов. В комнате две двери и два окна.

1. Измерьте общее расстояние (периметр) вокруг комнаты. (10 футов + 15 футов) x 2 = 50 футов
2. Умножьте периметр на высоту потолка, чтобы получить общую площадь стены: 50 футов.x 8 футов = 400 кв. футов
3. Двери обычно имеют площадь 21 квадратный фут (в данном примере их две): 21 квадратный фут x 2 = 42 квадратного фута.
4. Окна в среднем 15 квадратных футов (в данном примере их два): 15 квадратных футов x 2 = 30 квадратных футов
5. Возьмите общую площадь стены и вычтите площадь дверей и окон, чтобы поверхность стены была окрашена: 400 кв. Футов (площадь стены) — 42 кв. Фута (двери) — 30 кв. Футов (окна ) = 328 кв. Футов стен, которые необходимо покрасить.

Как правило, один галлон качественной краски обычно покрывает 400 квадратных футов.Одна кварта покрывает 100 квадратных футов. Поскольку в этом примере вам нужно покрыть 328 квадратных футов , одного галлона будет достаточно для нанесения одного слоя краски на стены. (Укрывистость будет зависеть от пористости и текстуры поверхности. Кроме того, для ярких цветов может потребоваться минимум два слоя.)

Покраска потолков

• Используя эмпирическое правило для покрытия, описанное выше, вы можете рассчитать количество краски, необходимое для потолка, умножив ширину комнаты на ее длину: 10 футов.x 15 футов = 150 кв. футов. Для этого потолка потребуется примерно два литра краски. (Для минимизации дефектов поверхности рекомендуется плоская отделка.)

Покраска дверей, окон и отделки

• Площадь дверей и окон рассчитана выше. (Неокрашенная область оконного стекла должна обеспечивать достаточное количество краски для любой отделки дверей и окон.) Определите обшивку плинтуса, взяв по периметру комнаты минус 3 фута на дверь (3 фута x 2 = 6 футов.) и умножьте это на среднюю ширину обрезки плинтуса, которая в этом примере составляет 6 дюймов (или 0,5 фута). 50 футов (периметр) — 6 футов = 44 фута 44 фута x 0,5 фута = 22 кв. Фута
• Добавьте область для дверей, окон и плинтуса. 42 кв. Фута (двери) + 30 кв. Футов (окна) + 22 кв. Фута (отделка плинтуса) = 94 кв. Фута
• Одной кварты будет достаточно для покрытия дверей, окон и обшивки в этом примере.

Совет: Перед покраской проветрите.Держите открытыми окно или внешнюю дверь в комнате, которую вы красите, чтобы не вдыхать ядовитые пары.

Теперь посмотрим, как выбрать и использовать кисть, и готово к делу!

Важность математических концепций Область

Площадь — это математический термин, определяемый как двумерное пространство, занимаемое объектом, отмечает Study.com, добавляя, что использование площади имеет множество практических применений в строительстве, сельском хозяйстве, архитектуре, науке и даже о том, сколько ковра вы получите. нужно укрыть комнаты в вашем доме.

Иногда площадь определить довольно просто. Для квадрата или прямоугольника площадь — это количество квадратных единиц внутри фигуры, говорится в «Рабочей тетради для 4-го класса Brain Quest». Такие многоугольники имеют четыре стороны, и вы можете определить площадь, умножив длину на ширину. Однако определение площади круга или даже треугольника может быть более сложным и требует использования различных формул. Чтобы по-настоящему понять концепцию площади и почему она важна для бизнеса, учебы и повседневной жизни, полезно взглянуть на историю математической концепции, а также на то, почему она была изобретена.

Исторические приложения

Некоторые из первых известных работ о местности пришли из Месопотамии, — говорит Марк Райан в «Геометрии для чайников, 2-е издание». Этот учитель математики в старшей школе, который также проводит семинары для родителей и является автором множества книг по математике, говорит, что месопотамцы разработали концепцию, касающуюся области полей и свойств:

«Фермеры знали, что если один фермер засевает площадь в три раза длиннее и вдвое шире, чем другой фермер, то более крупный участок будет в 3 x 2 или в шесть раз больше, чем у меньшего.»

Райан отмечает, что концепция площади имела множество практических применений в древнем мире и в прошлые века:

• Архитекторы пирамид в Гизе, которые были построены около 2500 г. до н.э., знали, насколько большой должна быть каждая треугольная сторона построек, используя формулу для определения площади двумерного треугольника.
• Китайцы умели вычислять площадь множества различных двумерных форм примерно к 100 г. до н. Э.
• Иоганн Кепплер, живший с 1571 по 1630 год, измерил площадь участков орбит планет, вращающихся вокруг Солнца, используя формулы для вычисления площади овала или круга.
• Сэр Исаак Ньютон использовал понятие площади для развития математического анализа.

Древние люди и даже те, кто дожил до Века Разума, имели множество практических применений для концепции площади. И эта концепция стала еще более полезной в практических приложениях, когда были разработаны простые формулы для определения площади различных двумерных форм.

Формулы для определения площади

Прежде чем приступить к практическому использованию концепции площади, вам сначала нужно знать формулы для нахождения площади различной формы.К счастью, для определения площади многоугольников используется множество формул, в том числе самые распространенные:

Прямоугольник

Прямоугольник — это особый тип четырехугольника, в котором все внутренние углы равны 90 градусам, а все противоположные стороны имеют одинаковую длину. Формула для определения площади прямоугольника:

где «A» представляет площадь, «H» — высоту, а «W» — ширину.

Квадрат

Квадрат — это особый тип прямоугольника, у которого все стороны равны.2, или площадь равна квадрату стороны.)

Треугольник

Треугольник — это трехсторонняя замкнутая фигура. Расстояние по перпендикуляру от основания до противоположной наивысшей точки называется высотой (H). Итак, формула будет такой:

где «A», как уже отмечалось, означает площадь, «B» — основание треугольника, а «H» — высоту.

Круг

Площадь круга — это общая площадь, ограниченная окружностью или расстоянием вокруг круга.Думайте о площади круга, как если бы вы нарисовали окружность и залили область внутри круга краской или мелками. Формула площади круга:

В этой формуле «A» — это, опять же, площадь, «r» представляет радиус (половина расстояния от одной стороны круга до другой), а π — греческая буква, произносимая «пи», что составляет 3,14 (отношение длины окружности к ее диаметру).

Практическое применение

Есть много реальных и реальных причин, по которым вам нужно будет рассчитать площадь различных форм.Например, предположим, что вы хотите засыпать газон дерном; вам нужно знать площадь вашего газона, чтобы купить достаточно дерна. Или вы можете застелить ковер в гостиной, холлах и спальнях. Опять же, вам нужно рассчитать площадь, чтобы определить, сколько коврового покрытия купить для разных размеров ваших комнат. Знание формул расчета площадей поможет вам определить площади комнат. 2

А = 3.2

A = 3,14 x 4 фута

A = 12,56 квадратных футов

Затем вы округлите эту цифру до 12,6 квадратных футов или даже 13 квадратных футов. Таким образом, вам понадобится 13 квадратных футов плитки, чтобы закончить пол в ванной.

Площадь треугольной комнаты

Если у вас действительно оригинально выглядящая комната в форме треугольника, и вы хотите застелить в ней ковер, воспользуйтесь формулой для определения площади треугольника. Сначала вам нужно измерить основание треугольника.Предположим, вы обнаружите, что основание составляет 10 футов. Вы должны измерить высоту треугольника от основания до вершины точки треугольника. Если высота пола вашей треугольной комнаты составляет 8 футов, вы должны использовать следующую формулу:

• A = ½ x B x H
• A = ½ x 10 футов x 8 футов
• A = ½ x 80 футов
• A = 40 квадратных футов

Итак, вам понадобится колоссальный 40 квадратных футов ковра, чтобы покрыть пол в этой комнате. Убедитесь, что на вашей карте достаточно средств на счете, прежде чем отправиться в магазин товаров для дома или ковров.

Что такое площадь? — Определение, факты и пример

Area Games

Area

Используйте единичные квадраты, чтобы понять концепцию площади и найти площадь для различных двухмерных форм.

охватывает Common Core Curriculum 3.MD.7Играть сейчасПосмотреть все игры по геометрии >>

Учитесь с полной программой обучения математике K-5

Что такое Area? В геометрии площадь можно определить как пространство, занимаемое плоской формой или поверхностью объекта. Площадь фигуры — это количество единичных квадратов, покрывающих поверхность замкнутой фигуры.Площадь измеряется в квадратных единицах, таких как квадратные сантиметры, квадратные футы, квадратные дюймы и т. Д.

Площадь приведенных ниже квадратов со стороной 1 сантиметр каждый будет измеряться в квадратных сантиметрах (см²).

Здесь площадь фигур ниже будет измеряться в квадратных метрах (м²) и квадратных дюймах (дюйм²).

Слово «площадь» происходит от латинского «площадь», что означает свободный участок ровной поверхности.Происхождение далее привело к неправильному получению площади как «определенного количества пространства, заключенного в пределах набора границ».

Мы часто находим площадь пола комнаты, чтобы определить размер покупаемого ковра. Покрытие пола плиткой, покрытие стен краской или обоями или строительство бассейна — это другие примеры, когда площадь вычисляется.

Обычные простые формы и многоугольники имеют свои собственные формулы для вычисления площади. Вот как вычисляется площадь обычных двухмерных или двумерных фигур:

Двумерные геометрические формы:

Название формы:	Изображение формы:	Формула площади:
Круг		Площадь = πr², где r радиус.
Треугольник		Площадь = bh, , где b — основание, А h — высота.
Квадрат		Площадь = l × l, где l — длина каждой стороны.
Прямоугольник		Площадь = l × w, , где l — длина и w — ширина.
Параллелограмм		Площадь = b × h, , где b — основание, , а h — высота по перпендикуляру.
Трапеция		Площадь = (a + b) h, , где a и b — длины параллельных сторон, , а h — высота по перпендикуляру.

В реальной жизни не каждую плоскую фигуру можно однозначно классифицировать как прямоугольник, квадрат или треугольник. Чтобы найти площадь составной фигуры, состоящей из более чем одной фигуры, нам нужно найти сумму площадей обеих или всех фигур, образующих составную фигуру.

Площадь внешней поверхности твердой или трехмерной формы называется площадью поверхности. Например, прямоугольная призма имеет 6 прямоугольных оснований и боковые грани. Итак, общая площадь поверхности — это сумма площадей всех 6 прямоугольников.

Интересные факты Среди всех фигур с одинаковым периметром круг имеет наибольшую площадь.

Давайте споем!

Для посадки овощей в саду,

Найдите площадь поля — все внутри.

Умножьте его длину на ширину,

И вот формула площади, которую вы применили!

Давайте сделаем это!

Вместо того, чтобы раздавать детям рабочие листы по математике, вовлекайте их в проекты по благоустройству дома. Сообщите им о комнате, которую вы собираетесь покрасить. Попросите их подсчитать общую площадь поверхности стен, чтобы узнать, сколько требуется краски.

Обсудите, как все стены в комнате могут отличаться друг от друга, и, таким образом, измерение общих размеров с последующим вычитанием площади двери, окон или книжных полок поможет оценить необходимое количество краски.