Площадь на высоту: Как найти объем через площадь 🚩 как найти высоту куба 🚩 Математика

Как найти Объем Параллелепипеда?

Поможем понять и полюбить математику

Начать учиться

300.1K

В 5 классе ученики знакомятся с объемными фигурами. Оглянитесь вокруг — мир состоит из параллелепипедов. Так что в любой непонятной ситуации просто ищите их объём. Давай научимся это делать. В статье найдете все необходимые формулы и правила.

Понятие объема

Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.

Объём — это количественная характеристика пространства, занимаемого телом или веществом.

Другими словами, это то, сколько места занимает предмет.

Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.

За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см³), кубический миллиметр (1 мм³), кубический метр (1 м³).

Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.

Два свойства объёма У равных тел равные объёмы. Например, у двух одинаковых пакетов сока равные объемы. Если геометрическое тело состоит из нескольких геометрических тел, то его объём равен сумме объёмов этих тел.

Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.

Реши домашку по математике на 5.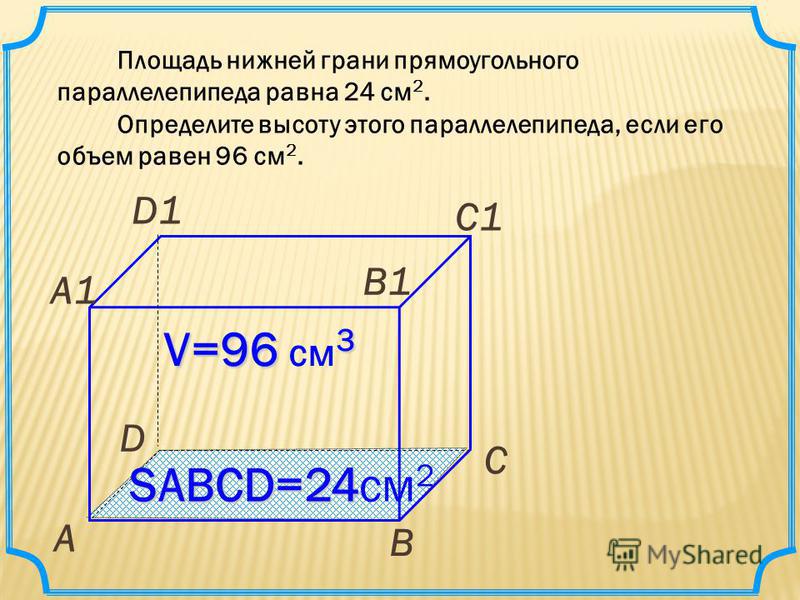

Подробные решения помогут разобраться в самой сложной теме.

Объем прямоугольного параллелепипеда

Параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом.

Прямоугольным параллелепипедом

называют параллелепипед, у которого все грани являются прямоугольниками.

Формула объема прямоугольного параллелепипеда Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты: V = a × b × h

Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.

a	длина параллелепипеда
b	ширина параллелепипеда
h	высота параллелепипеда
P (осн)	периметр основания
S (осн)	площадь основания
S (бок)	площадь боковой поверхности
S (п. п.)	площадь полной поверхности
V	объем

Пример 1. Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см.

a = 9 см

b = 6 см

h = 3 см

V = a × b × h

V = 9 × 6 × 3 = 162 см³.

Ответ: объем прямоугольного параллелепипеда равен 162 см³.

Следствие Объем параллелепипеда равен произведению площади основания на высоту. V = Sосн × h

Из этого следствия выведем формулу нахождения площади основания параллелепипеда.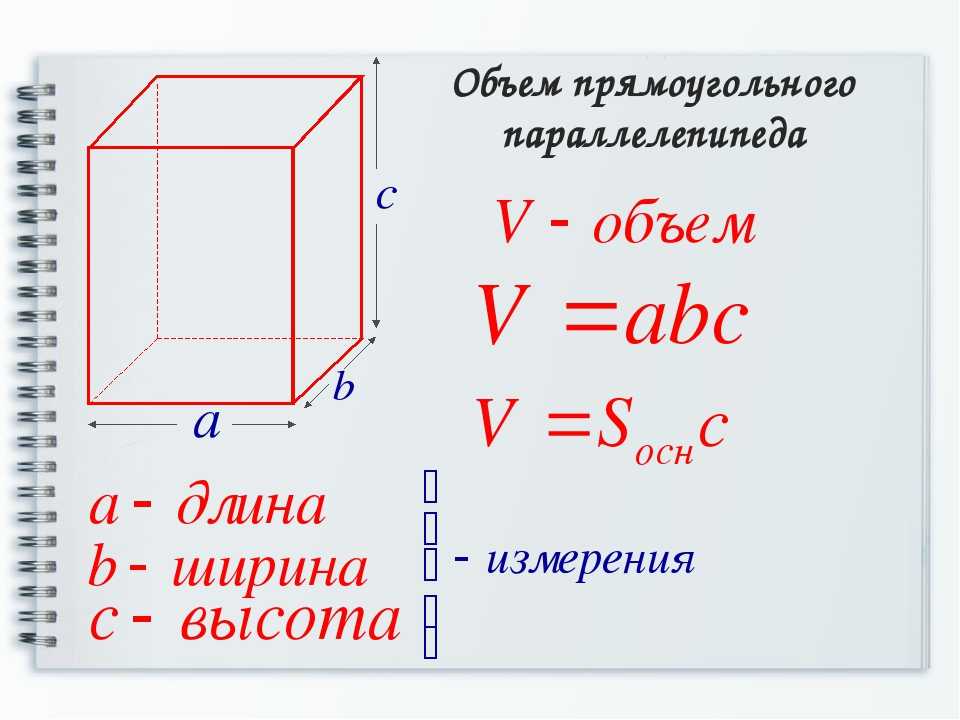

S_осн = V : h

Пример 2. Найдите площадь основания параллелепипеда, если его объем равен 96 см³, а высота 8 см.

V = 96 см

3

h = 8 см

V = S_осн × h

S_осн = V : h

S_осн = 82 см³ : 8 см = 12 см².

Ответ: площадь основания параллелепипеда равна 12 см².

Обучение на курсах по математике в онлайн-школе Skysmart поможет быстрее разобраться в теме и правильно решать задачки!

Вычисление площади

Как вы уже поняли, вычисление объёма параллелепипеда напрямую зависит от вычисления его площади. Давайте разберемся, сколько всего площадей можно найти в параллелепипеде.

Чтобы найти площадь боковой поверхности параллелепипеда, вычислите по отдельности площадь каждой боковой грани, а затем найдите сумму получившихся значений.

Так как противолежащие грани прямоугольного параллелепипеда одинаковые, то получим формулу:

• S_{б. п.} = 2 (ac + bc)

Чтобы вычислить площадь полной поверхности параллелепипеда, сложите площадь боковой поверхности и две площади основания. Так как площади оснований у прямоугольного параллелепипеда одинаковые, то получим формулу:

• S_{п. п.} = 2 (ab + ac + bc)

Пример 3. Найдем площадь поверхности параллелепипеда, если длина основания равна 6 сантиметров, ширина — 4 см соответственно, а высота — 3 см.

S_{п. п.} = 2 (ab + ac + bc)

S_{п. п.} = 2 (6 × 4 + 6 × 3 + 4 × 3) = 2 × (24 + 18 + 12) = 2 × 54 = 108 см².

Ответ: площадь поверхности параллелепипеда — 108 см².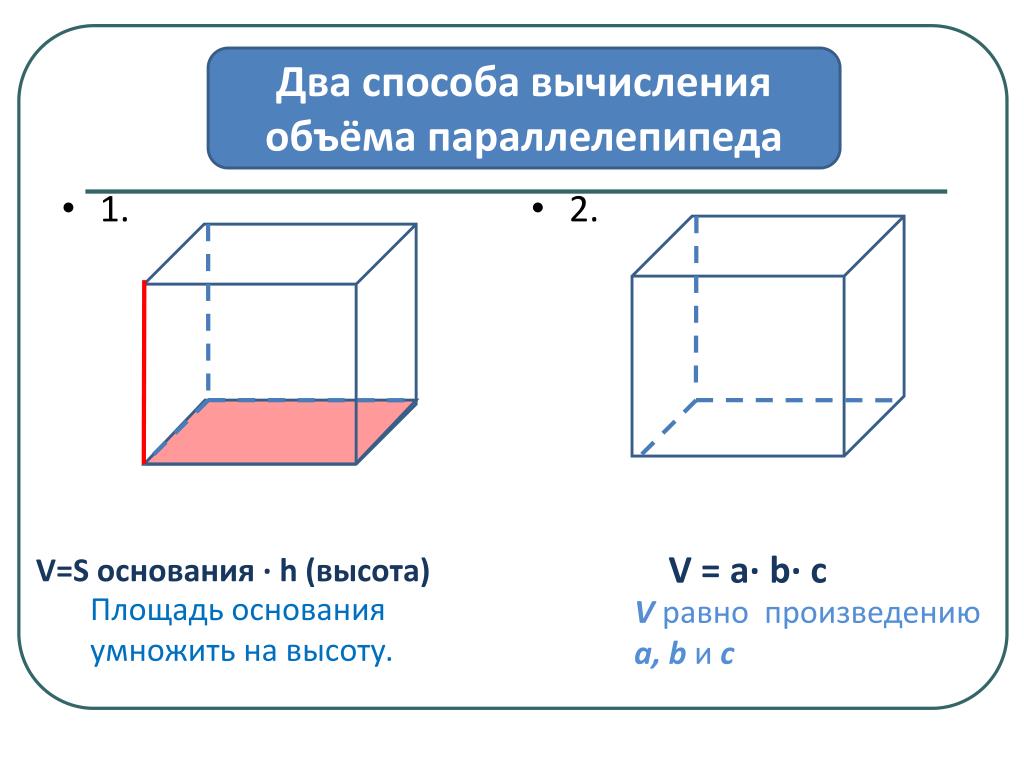

Как видите, вычислить объём и найти площадь параллелепипеда совсем не трудно.

Задачи на самопроверку

Пользоваться онлайн-калькуляторами можно, когда вы уже натренировались в решении задачек и с закрытыми глазами можете вычислить объем любого параллелепипеда. Давайте разберем еще несколько примеров.

Задачка 1. Найдите объём параллелепипеда со сторонами 18 см, 10 см, 7 см.

Как решаем:

a = 18 см

b = 10 см

h = 7 см

Формула нахождения объема параллелепипеда:

V = a × b × h

Подставляем наши числа:

V = 18 × 10 × 7 = 1260 см³.

Ответ: объём параллелепипеда равен 1260 см³.

Задачка 2. Найдите площадь основания параллелепипеда, если его объём равен 120 см

3, а высота — 15 см.

Как решаем:

V = 120 см

h = 15 см

V = S_осн × h

S_осн = V : h

S_осн = 120 см³: 15 см = 8 см².

Ответ: площадь основания параллелепипеда равна 8 см².

Задачка 3. Найдите площадь полной поверхности прямоугольного параллелепипеда, если длина основания равна 30 сантиметров, ширина равна 12 см, а высота равна 5 см.

Как решаем:

S_{п. п.} = 2 (ab + ac + bc)

S_{п. п.} = 2 (30 × 12 + 30 × 5 + 12 × 5) = 2 × (360 + 150 + 60) = 2 × 570 = 1140 см²

.

Ответ: площадь полной поверхности параллелепипеда равна 1140 см².

Пусть все необходимые формулы будут под рукой в нужный момент. Сохраняйте табличку-шпаргалку на гаджет или распечатайте ее и храните в учебнике.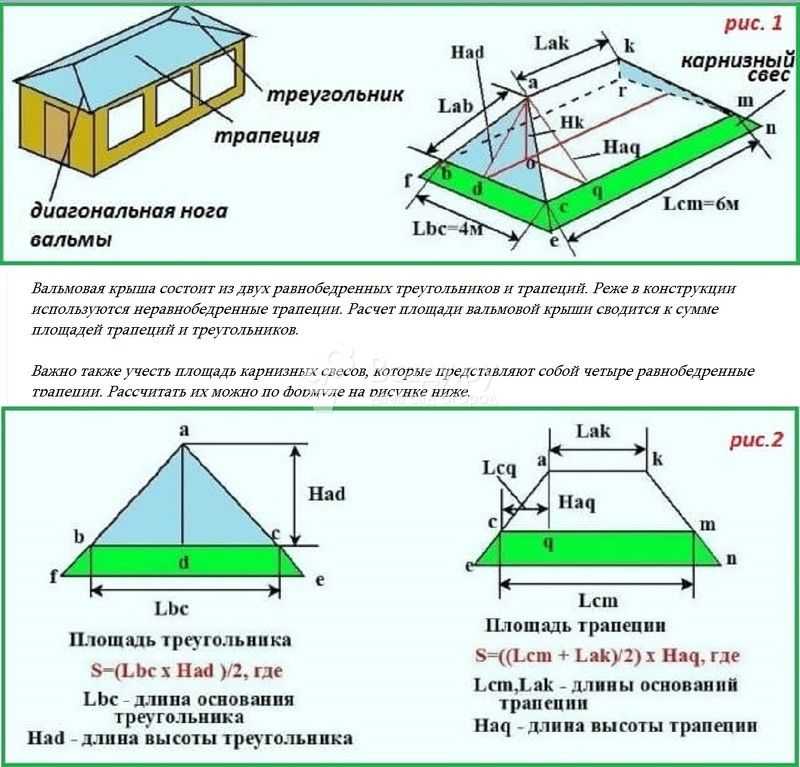

V параллелепипеда	V = a × b × h
	V = Sосн × h
S боковой поверхности	Sб. п. = 2 (ac + bc)
S полной поверхности	Sп. п. = 2 (ab + ac + bc)

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Анастасия Белова

К предыдущей статье

399.1K

Время, скорость, расстояние

К следующей статье

486. 7K

Порядок действий в математике

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Калькулятор расчета объема резервуара и перевод литров в кубы в ООО ЗРК

Перевод литров в кубы

Выберете среду: ВодаБензинМолокоДиз. топливоМаслоНефтьСпирт

Введите объем в литрах:

Единица измерения объема – это кубический метр. Данный факт относится к числу общепринятых аксиом. Сторона этого куба равна одному метру. Этот показатель принято использовать, если необходимо определить объем бака, резервуара, либо цистерны. Определенные трудности вызывает расчет в связи с тем, что жидкости принято мерить в литрах.

Пытаясь рассчитать величину актуального для хранения и сохранения жидкой субстанции резервуара либо цистерны, нужно учесть еще и вес вещества. Он не соответствует количеству литров.

Расчет объема резервуара

Выберите форму: ПрямоугольнаяЦилиндрическая

Длина в метрах:

Ширина в метрах:

Высота в метрах:

Всем, кто прилежно изучал школьный курс физики, известно, что минимальной площадью поверхности при максимальном объеме обладает сосуд в форме шара. Но шарообразные емкости сложны в изготовлении и непрактичны, поэтому производители изготавливают емкости в форме цилиндра или куба (прямоугольника).

ЦИЛИНДРИЧЕСКИЕ ЕМКОСТИ

Могут располагаться горизонтально или вертикально. Объем рассчитывается по формуле V=πr2h. То есть умножаем число π (3,14159) на радиус в квадрате и на высоту h цилиндра.

Пример: есть вертикальный цилиндрический резервуар диаметром 3 метра и высотой 5 метров. Рассчитываем объем: Радиус – 1,5 метра, в квадрате будет 2,25.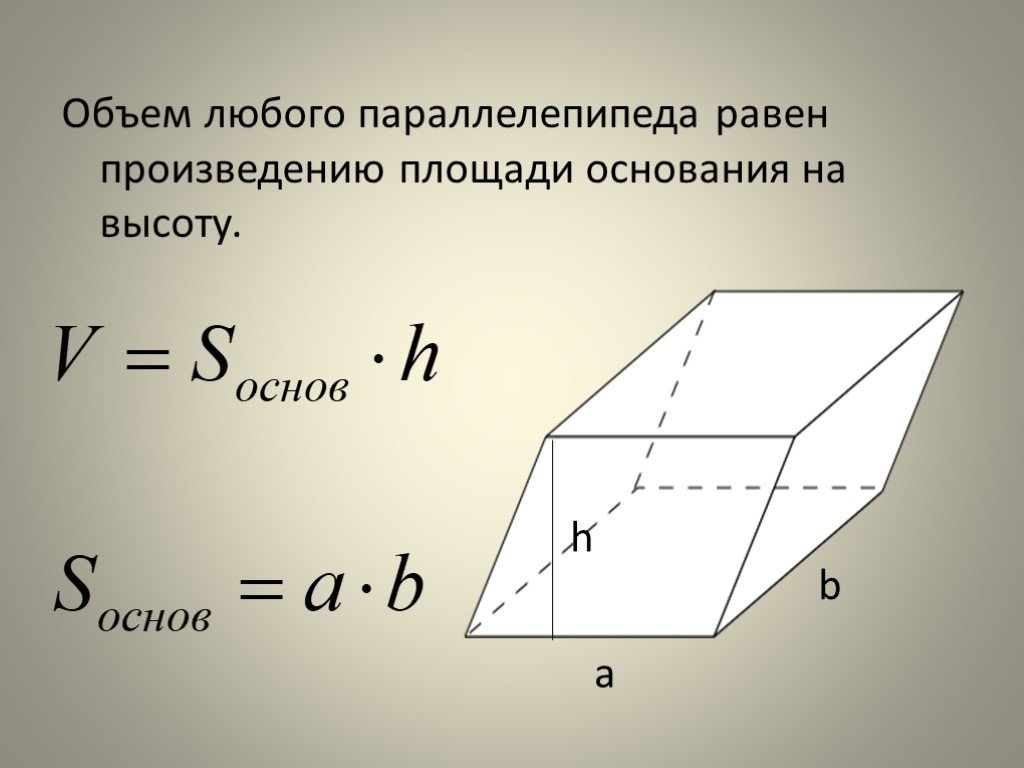 Умножаем: 3,14159 ×2.25 ×5 (высота) = 35,34 м3. Итого, рабочий объем нашего резервуара будет равен 35 кубическим метрам, или 35 000 литрам (в 1 кубе – 1000 литров).

На практике конкретные размеры резервуара рассчитываются с учетом его функциональности. Например, горизонтальный резервуар диаметром 1 метр и длиной 10 метров будет просто неудобен в использовании. Его объем составит 7,8 куба. Если нам нужен резервуар такого объема, уместнее увеличить его диаметр и уменьшить длину – например, сделать диаметр 2 метра при длине 3 метра. Получим те же 7,8 куба при гораздо более функциональных размерах.

ПРЯМОУГОЛЬНЫЕ ЕМКОСТИ

Здесь все еще проще. Чтобы узнать полный объем, достаточно длину емкости умножить на ее ширину и высоту. Например, кубический резервуар со стороной 1 метр будет вмещать 1 куб жидкости. Емкость размером 3000 мм × 2000 мм × 2500 мм будет иметь объем 15 кубометров.

Почему большинство резервуаров имеют не квадратную или прямоугольную, а цилиндрическую форму? Потому что конструктивно такие емкости являются более прочными. Чтобы сварить куб, нужны 6 листов стали и 12 сварных швов. Цилиндрическая емкость имеет всего 3 поверхности: два круглых дна и цилиндрический корпус.

Корпус может быть сварен из одного листа металла, свернутого в цилиндр, для этого нужен всего 1 сварной шов. Плюс еще два круговых шва, чтобы приварить днища. Итого, в идеальном варианте всего 3 сварных шва – вместо 12 у куба.

Зачем тогда делают прямоугольные емкости? У них есть свои сферы использования. Например, их применяют в качестве пожарных емкостей – они обладают отличной эргономикой и хорошо вписываются в помещения, занимая минимум места.

В нашей компании вы можете заказать резервуар практически любого типа, формы и назначения. Мы предлагаем как типовые варианты, так и изготавливаем продукцию на заказ. Зная основные принципы расчета размеров и объема резервуаров, вы можете оценить, какой вариант для вас окажется наиболее подходящим.

Выбрать подходящую ёмкомсть в каталоге, производство металлических ёмкостей для разных задач.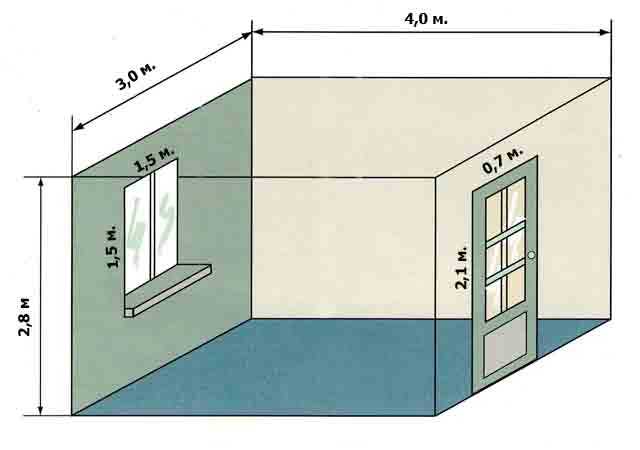

Калькулятор площади поверхности тела

Приведенный ниже калькулятор вычисляет общую площадь поверхности человеческого тела, называемую площадью поверхности тела (ППТ). Прямое измерение BSA затруднено, поэтому было опубликовано множество формул, оценивающих BSA. Калькулятор ниже предоставляет результаты для некоторых из самых популярных формул.

Калькулятор связанных областей | Калькулятор площади поверхности

Таблица средних значений BSA

BSA часто используется в клинических целях в сравнении с массой тела, поскольку это более точный показатель метаболической массы (потребности организма в энергии). Метаболическую массу можно оценить с помощью безжировой массы, где безжировая масса представляет собой всю массу тела человека, не включая жир. Сюда входят кости, сухожилия, внутренние органы, мышцы, кровь, нервы и многое другое. Поскольку жировые отложения не являются метаболически активными, а безжировая масса исключает жировые отложения, безжировая масса является разумной оценкой метаболической массы.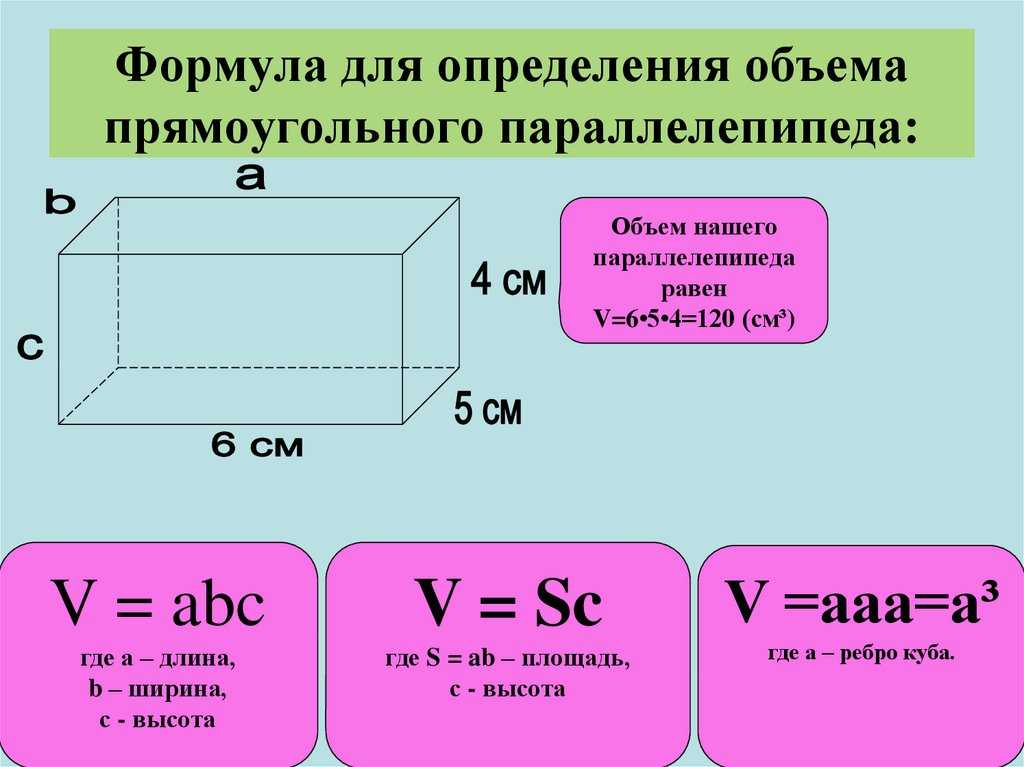

BSA также используется в различных других клинических условиях, таких как определение сердечного индекса (чтобы соотнести работу сердца человека с размером его тела) или, чаще всего, дозировка для химиотерапии (категория лечения рака). В то время как дозировка для химиотерапии часто определяется с использованием BSA пациента, существуют аргументы против использования BSA для определения дозировок лекарств, имеющих узкий терапевтический индекс — сравнение количества вещества, необходимого для получения терапевтического эффекта, с количеством, которое необходимо для достижения терапевтического эффекта. вызывает интоксикацию. Если терапевтический индекс слишком узок, БСА может быть недостаточно точным показателем, и возникает риск вызвать токсический, а не терапевтический эффект. Есть также свидетельства того, что BSA становится менее точным при крайних значениях роста и веса, и ИМТ может быть более точной оценкой в ​​таких случаях. Несмотря на эти ограничения, эффекты химиотерапевтических доз, определяемые измерениями BSA, по-прежнему остаются более стабильными, чем эффекты, определяемые только массой тела.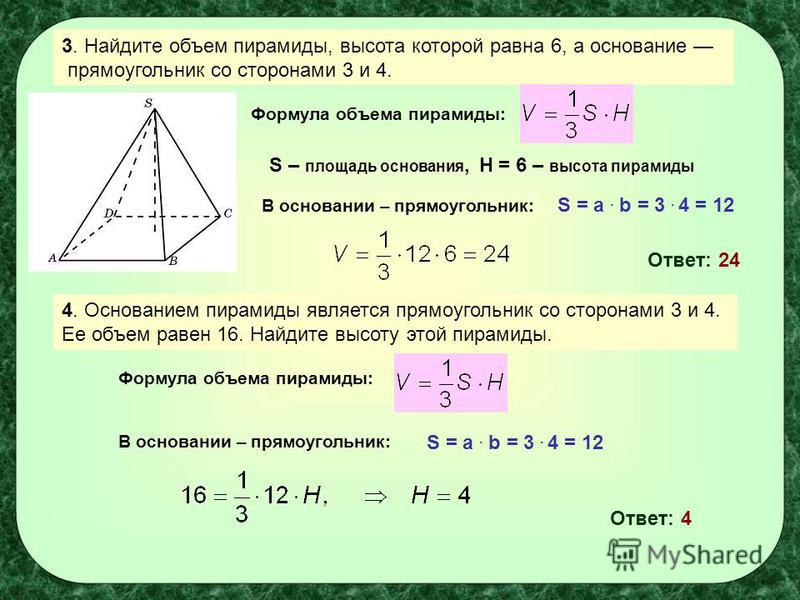

Ниже приведены некоторые из наиболее популярных формул для оценки BSA и ссылки на справочные материалы по каждой из них для получения дополнительной информации об их выводах. Наиболее широко используемой из них является формула Дюбуа, которая, в отличие от индекса массы тела, показала свою эффективность для оценки жировых отложений как у пациентов с ожирением, так и у пациентов без ожирения. Где BSA представлено в м ² , W — вес в кг , а H — рост в см , формулы будут следующими:

Формула Дюбуа:

BSA = 0,007184 × W ^0,425 × H ^0,725

Du Bois D, Du Bois EF (июнь 1916 г.). «Формула для оценки приблизительной площади поверхности, если известны рост и вес». Архив внутренней медицины 17 (6): 863-71. PMID 2520314 . Проверено 9 сентября 2012 г.

Формула Мостеллера:

BSA = = 0,016667 × Ш ^0,5 × В ^0,5

Мостеллер РД. «Упрощенный расчет площади поверхности тела».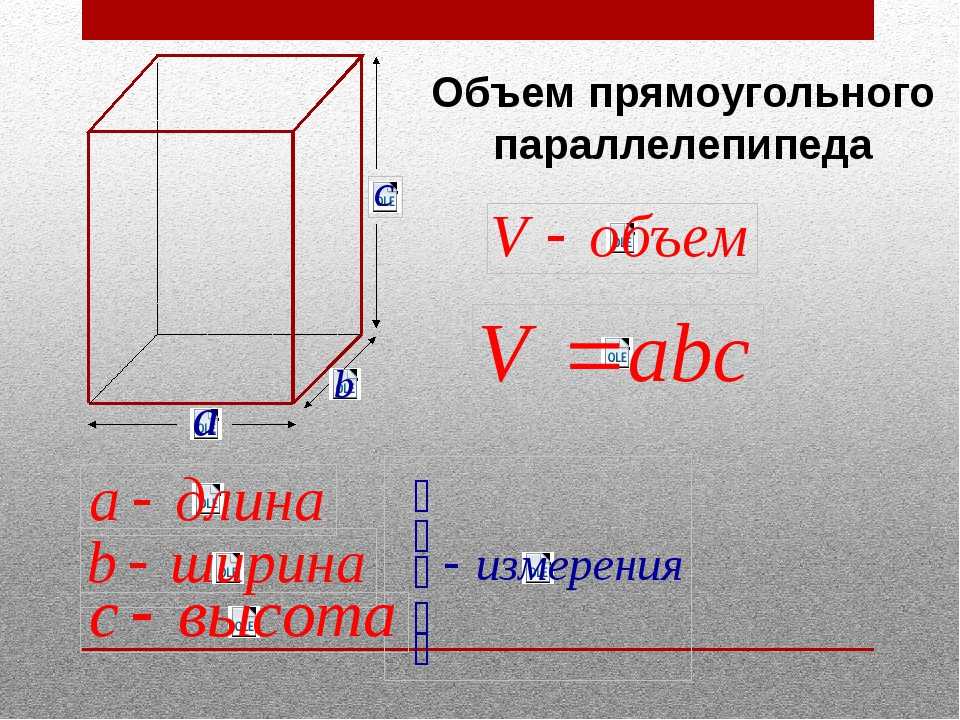 N Engl J Med 1987; 317:1098. PMID 3657876.

ФОРМУЛА HAYCOCK:

BSA = 0,024265 × W ^0,5378 × H ^0,3964

Haycock GB, Schwartz GJ, Wisotscy Dhomet-Formememememet Surformicke DHAMET-FORMIT-FORMETMELIRIRIC. у младенцев, детей и взрослых» J Pediatr 1978, 93:62-66.

Формула Гехана и Джорджа:

BSA = 0,0235 × W ^0,51456 × H ^0,42246

Gehan EA, George SL, Cancer Chemother Rep 1970, 54:225-235

Формула Бойда:

BSA = 0,03330 × W ^{(0,6157 — 0,0188 × log10(W)} × H ^0,9

3). Площадь поверхности человеческого тела, Миннесотский университет, Институт защиты детей, Серия монографий, № х, Лондон: Oxford University Press

Формула Фудзимото:

BSA = 0,008883 × Ш ^0,444 × В ^0,663

Фудзимото С., Ватанабэ Т., Сакамото А., Юкава К., Моримото К. Исследования площади физической поверхности японцев 18.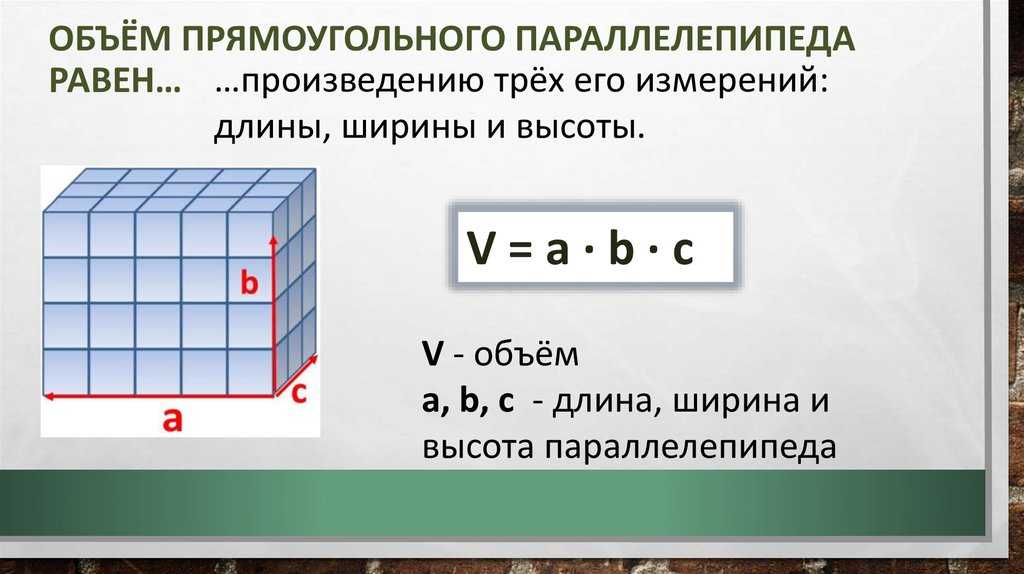 Формулы расчета в три этапа для всех возрастов Nippon Eiseigaku Zasshi 1968;5:443-50.

Формула Такахиры:

BSA = 0,007241 × W ^0,425 × H ^0,725

Fujimoto S, Watanabe T, Sakamoto K., Moroto K. Исследования физической поверхности Японии, Морото К. 18. Формулы расчета в три этапа для всех возрастов. Nippon Eiseigaku Zasshi 1968; 5:443-50.

Формула Шлиха:

Женщины BSA = 0,000975482 × W ^0,46 × H ^1,08

Мужчины BSA = 0,000579479 × Ш ^0,38 × В ^1,24

Шлих Э., Шумм М., Шлих М.: «3-D-сканирование тела с антропометрическими данными, проверенными для лучшего иммунитета специальных корпораций». Ernahrungs Umschau 2010;57:178-183

Калькулятор BSA — площадь поверхности тела

Калькулятор BSA позволяет легко найти площадь поверхности тела (BSA), которая представляет собой площадь внешней поверхности человеческого тела, выраженную в квадратных метрах. Если вы знаете, как рассчитать BSA, вы найдете его очень полезным в медицине и физиологии, так как является более точным показателем обмена веществ, чем масса тела . Вот почему многие врачи основывают свои рецепты на формуле BSA.

Однако вам может быть просто интересно вычислить площадь поверхности вашего тела. Ученые установили, что вся кровеносная система человека более чем в два раза длиннее окружности Земли, если ее растянуть. Если вы знаете, как рассчитать BSA, вы можете узнать, сколько квадратных метров занимала бы поверхность вашего тела, если бы его можно было распутать и разложить. Мы надеемся, что вы найдете это более интересным, чем болезненным.

Продолжайте читать, если хотите узнать:

• Что такое формула BSA и как ее можно использовать для расчета площади тела;
• Что такое калькулятор площади поверхности тела;
• Как рассчитать BSA;
• Другие калькуляторы, на которые стоит обратить внимание, если вам интересна эта тема.

Отказ от ответственности : Мы делаем все возможное, чтобы наши омни-калькуляторы были максимально точными и надежными. Однако этот инструмент никогда не сможет заменить профессиональную медицинскую консультацию.

Формула BSA

Для расчета площади поверхности тела можно использовать множество различных формул. Наш калькулятор BSA по умолчанию использует наиболее распространенную форму, формулу Дюбуа.

Однако в расширенном режиме существует множество различных формул BSA (Mosteller, Haycock, Gehan and George, Boyd, Fujimoto, Takahira, Shuter и Aslani и Schlich, отдельно для мужчин и женщин).

Все, что вам нужно для использования любой из этих формул, это ваш вес и рост. Давайте взглянем на некоторые из них. 9{0,663}BSA=0,008883×вес0,444×высота0,663

, где BSA измеряется в квадратных метрах, вес в килограммах и рост в сантиметрах. Наш инструмент позволяет легко использовать другие единицы измерения, так что не беспокойтесь.

Давайте попробуем рассчитать по формуле Мостеллера:

1. Возьмем ваш рост в сантиметрах, например, 170 .
2. Укажите свой вес в килограммах, например, 60 .
3. Умножьте свой рост на свой вес, 170 × 60 = 10200 .
4. Разделить результат на 3600, 10200/3600 = 2,8 .
5. Найдите квадратный корень из результата, SQRT 2,8 = 1,67 .

Если ваш рост 170 см, а вес 60 кг, приблизительный расчет площади поверхности вашего тела составит 1,67 метра в квадрате.

Некоторые практикующие врачи предпочитают другие формулы BSA, такие как Haycock или Gehan & George.

Зачем использовать этот калькулятор площади поверхности тела?

К счастью для вас, нет необходимости самостоятельно рассчитывать BSA. Вы можете избежать утомительных вычислений, воспользовавшись калькулятором площади поверхности тела. Благодаря этому инструменту вы можете найти размер своего тела, как если бы это была плоская поверхность. Хотя калькулятор основан на некоторых сложных уравнениях, он прост в использовании и занимает всего несколько секунд, если вы уже знаете свой рост и вес.

Оказывается, знание того, как рассчитать BSA, может дать вам представление об уровне вашего здоровья, чего не могут другие показатели. Например, площадь поверхности вашего тела является предиктором уровня кальция в коронарных артериях, что является серьезной медицинской проблемой. Это делает BSA лучше, чем индекс массы тела, поскольку, хотя он и хорош для анализа вашего общего состояния здоровья на основе веса, ИМТ не может предсказать это состояние.

Как рассчитать BSA

Самый простой способ рассчитать площадь поверхности тела — воспользоваться нашим калькулятором BSA. Этому инструменту нужны только ваш вес и рост, чтобы решить уравнение. После подстановки этих двух значений вы автоматически получите результат.

Давайте проверим наш предыдущий пример:

1. Вес (кг): 60
2. Высота (см): 170

При этих измерениях площадь поверхности вашего тела составляет примерно 1,69 квадратных метра.

Если вы собираетесь рассчитать BSA, полезно знать средние значения BSA. Они делятся на возрастные и гендерные категории.

Средняя площадь поверхности тела для:

• Младенцы: 0,25 м²
• Дети от 2 лет: 0,5 м²
• Дети от 10 лет: 1,14 м²
• Женщины: 1,6 м²
• Мужчины: 1,9 м²

Прочие соображения

Если вас интересуют различные измерения, связанные с вашим телом, вам также следует воспользоваться нашим калькулятором ИМТ . Это инструмент, который вы можете использовать, чтобы узнать, находится ли ваш вес в пределах нормы или нет. Еще один калькулятор, который может оказаться полезным, — это наш калькулятор потребления воды.

Стоит отметить, что, хотя БСА является хорошим индикатором скорости метаболизма, он подвергся некоторой критике. Наиболее важным из них является использование его для определения дозировки лекарств, которые не имеют большого права на ошибку, таких как химиотерапия.

Часто задаваемые вопросы

Как рассчитать BSA при весе 163 фунта и росте 5 футов 4 дюйма?

BSA – площадь поверхности тела – равна 1,8 м ² .

Для расчета:

1. Преобразуйте вес в кг, разделив их на 2,2046.

   163/2,2046 = 73,94 кг

2. Преобразовать высоту в дюймы, а затем в см (умножив на 2,54).

   5 футов 4 дюйма = 64 дюйма
   64 × 2,54 = 162,56 см

3. Используйте, например, формулу Дюбуа .

   BSA = 0,007184 × вес ^0,425 × высота ^0,725

4. Подстановка значений:

   BSA = 0,007184 × 73,94 ^0,425 × 162,56 ^0,725 = 1,7932 м ²

Как рассчитать BSA для педиатрии?

Для расчета ППТ для педиатрии (дети) можно использовать те же формулы, что и обычно. Например, популярный вариант формула Мостеллера . Для его использования:

1. Измерьте вес ребенка (в килограммах – кг).
2. Проверить ребенка высота или длина (в сантиметрах – см).
3. Умножьте на вес и рост.
4. Разделить результат на 3600 .
5. Найдите квадратный корень из этого числа.
6. Готово! Вы всегда можете перепроверить с помощью нашего калькулятора BSA.

Что означает BSA 1,73?

BSA, равный 1,73, означает, что площадь поверхности тела равна0015) .

Это значение часто упоминается как справочное значение, поскольку оно представляет собой расчетную площадь поверхности тела человека массой 70 кг (таким образом – «средний взрослый» ). Он также используется для оценки СКФ – скорости клубочковой фильтрации.

Как рассчитать площадь поверхности тела в дюймах и фунтах?

Вы можете использовать модифицированную формулу Мостеллера для расчета площади поверхности тела (ППТ) в дюймах и фунтах.