Расчет деревянной балки перекрытия согласно СП 64.13330.2011
Примечание: Если нагрузка на балку вам уже известна, а вникать в теоретические основы расчета у вас нет никакого желания, то можете сразу воспользоваться калькулятором. Впрочем воспользоваться калькулятором можно и после того, как определены нагрузка и расчетное сопротивление.
Итак планируется междуэтажное перекрытие по деревянным балкам для дома, имеющего следующий план:
Рисунок 515.1. План помещений второго этажа.
1. Общий Расчет балки перекрытия санузла на прочность
Для того, чтобы рассчитать деревянную балку на прочность согласно требований СП, следует сначала определить множество различных данных на основании общих положений расчета балок.
1.1. Виды и количество опор
Деревянные балки будут опираться на стены. Так как мы не предусматриваем никаких дополнительных мер, позволяющих исключить поворот концов балки на опорах, то опоры балки следует рассматривать, как шарнирные (рисунок 219.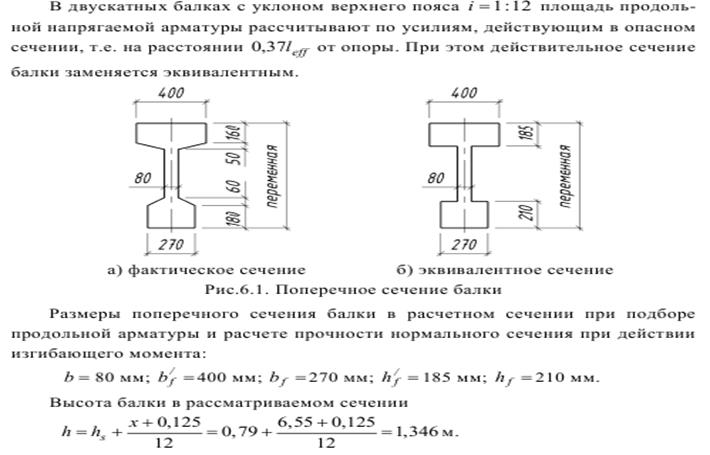
Рисунок 219.2.
Примечание: Так как концы балок, опирающиеся на каменные стены, для уменьшения риска гниения балок как правило обрабатывают гидроизоляционными материалами, имеющими относительно малый модуль упругости, при этом глубина заделки концов балки в стену не превышает 15-20 см, то даже если на опорные участки таких балок будет опираться каменная кладка, то это все равно не позволяет рассматривать такое опирание, как жесткое защемление.
1.2. Количество и длина пролетов
Согласно плану, показанному на рисунке 515.1, для перекрытия в санузле (помещение 2-1) длина пролета будет составлять около:
l = 4.18 — 0.4 = 3.78 м
При этом балки будут однопролетными, а значит статически определимыми.
1.3. Система координат
Расчет будем производить используя стандартную систему координат с осями х
, у и z.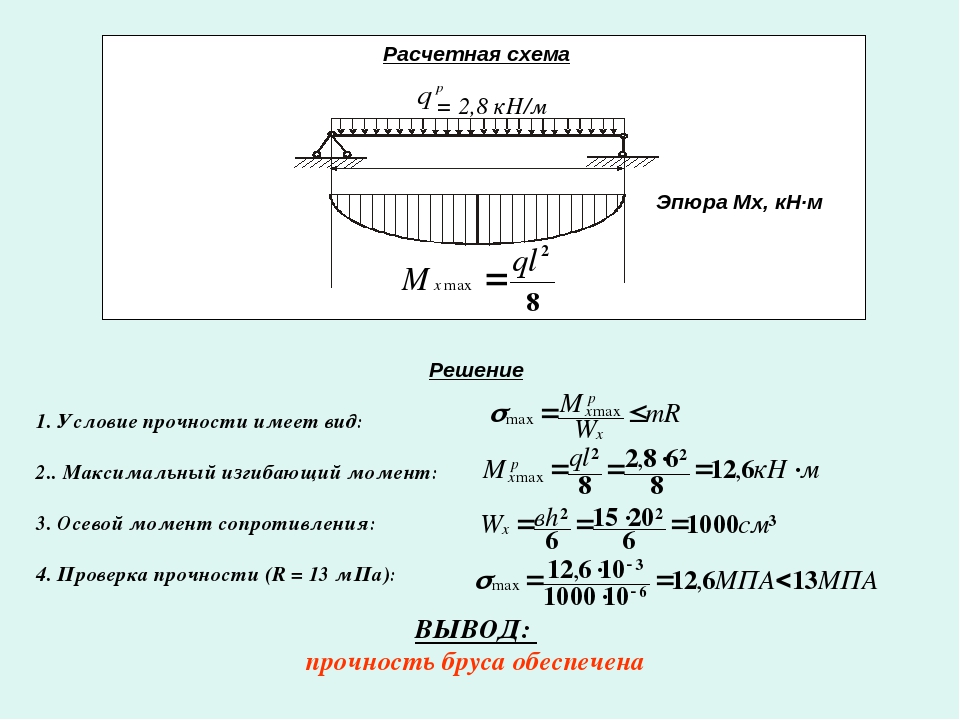 При этом балка рассматривается как стержень, нейтральная ось которого совпадает с осью координат х, а начало координат совпадает с началом балки. Соответственно длина балки измеряется по оси х.
При этом балка рассматривается как стержень, нейтральная ось которого совпадает с осью координат х, а начало координат совпадает с началом балки. Соответственно длина балки измеряется по оси х.
1.4. Действующие нагрузки
Все возможные расчетные плоские нагрузки для такого перекрытия мы уже собрали:
qрп = 212.46 кг/м2
qрв = 195 кг/м2
Примечание: при объемной чугунной ванне, установленной посредине балок перекрытия, расчетное значение временной нагрузки может быть значительно больше.
Однако такие значения нагрузок можно использовать только при расчете монолитного перекрытия. В нашем же случае балки перекрытия представляют собой крайние или промежуточные опоры для многопролетных балок — досок настила и остального пирога перекрытия.
Таким образом для более точного определения нагрузки на наиболее загруженную балку следует точно знать, доски какой длины будут использоваться в качестве настила по балкам. Если такого знания нет, то я рекомендую рассматривать наиболее неблагоприятный вариант, а именно — доски будут перекрывать 2 пролета, т.е. опираться на 3 балки перекрытия.
Если такого знания нет, то я рекомендую рассматривать наиболее неблагоприятный вариант, а именно — доски будут перекрывать 2 пролета, т.е. опираться на 3 балки перекрытия.
В этом случае наиболее нагруженной будет балка — промежуточная опора для таких досок — двухпролетных балок, соответственно значения нагрузок для такой балки следует увеличить в 10/8 = 1.25 раза или на 25%, тогда:
qрп = 212.46·1.25 = 265.58 кг/м2
qрв = 195·1.25 = 243.75 кг/м2
Если доски будут перекрывать 3 пролета, то значения нагрузок следует увеличить в 1.1 раза (253.4.4). При 4 пролетах — в 8/7 = 1.15 раза (262.7.10) и так далее, тем не менее остановимся на первом варианте, так оно надежнее.
Так как на рассчитываемое перекрытие действует только одна кратковременная нагрузка (особые нагрузки типа взрывной волны или землетрясения мы для нашего перекрытия не предусматриваем), то при рассмотрении основного сочетания нагрузок используется полное значение кратковременной нагрузки согласно СП 20. 13330.2011 «Нагрузки и воздействия» п.1.12.3, тогда:
13330.2011 «Нагрузки и воздействия» п.1.12.3, тогда:
qр = 265.58 + 243.75 = 509.33 кг/м2
Так как балки рассчитываются не на плоскую, а на линейную нагрузку, то при шаге балок 0.6 м расчетная линейная нагрузка на балку составит:
qрл = 509.33·0.6 = 305.6 кг/м
1.5. Определение опорных реакций и максимального изгибающего момента
Так как загружение балки равномерно распределенной нагрузкой — достаточно распространенный частный случай, то для определения опорных реакций можно воспользоваться готовыми формулами:
А = В = ql/2 = 305.6·3.78/2 = 577.6 кг
Мmax = ql2/8 = 305.6·3.782/8 = 545.82 кгм или 54582 кгсм
1.6. Построение эпюр поперечных сил и изгибающих моментов
В нашем частном случае, когда нагрузка является равномерно распределенной, можно опять же воспользоваться готовыми эпюрами, благо их для такого случая построено уже множество:
Рисунок 149.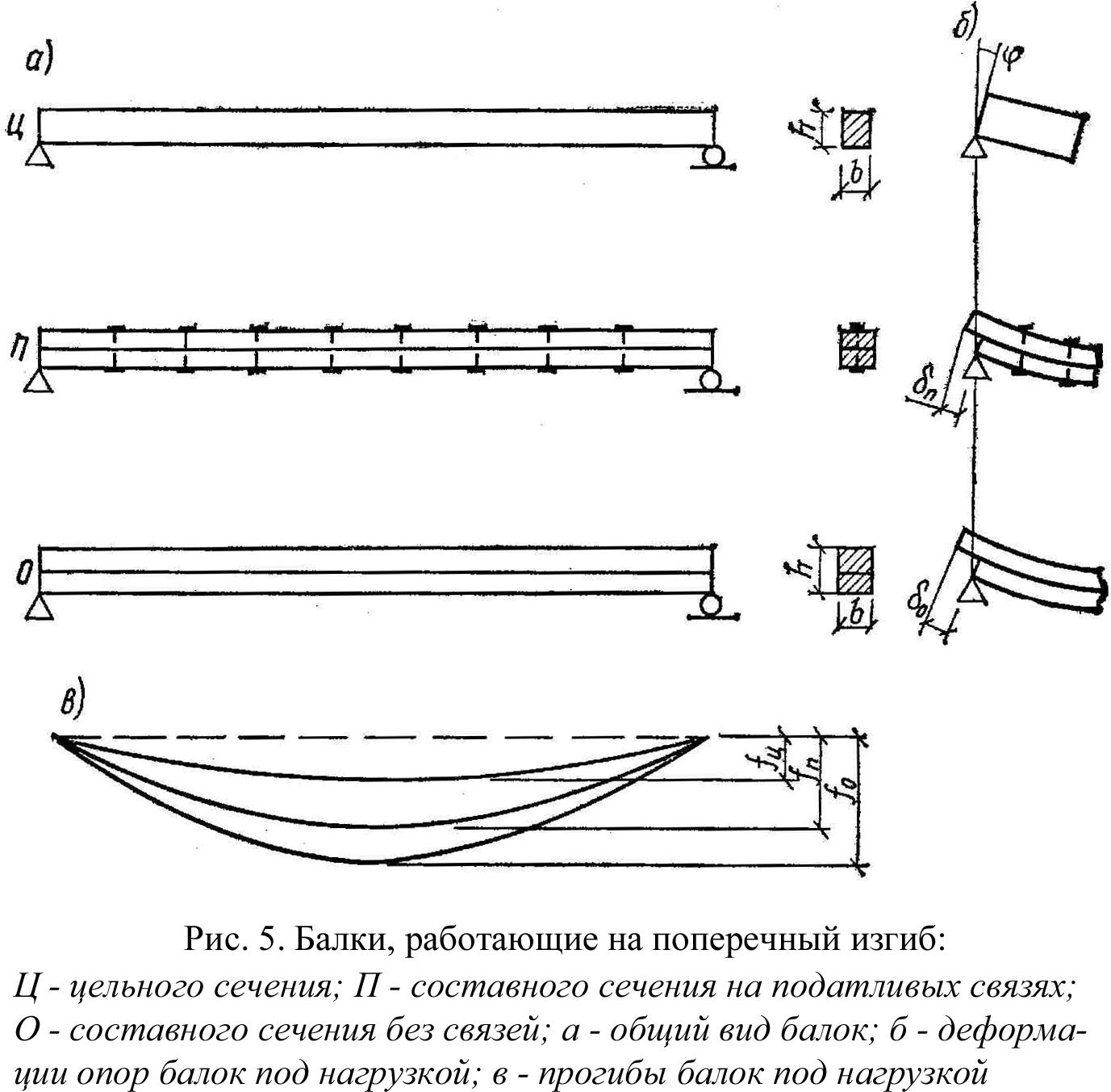 7.2. Эпюры поперечных сил и моментов, действующих в поперечных сечениях
7.2. Эпюры поперечных сил и моментов, действующих в поперечных сечениях
Для большей наглядности можно нанести полученные значения поперечных сил (опорные реакции — это и есть значения поперечных сил в начале и в конце балки) и максимального изгибающего момента на эпюры.
Примечание: В данном случае эпюра моментов помечена знаком минус, просто потому, что откладывается снизу от оси координат х. А вообще знак для моментов принципиального значения не имеет, так как при действии момента всегда есть и растянутая и сжатая зона поперечного сечения. Таким образом наиболее важно понимать, где при действии момента будет растянутая, а где сжатая зона сечения. Впрочем для деревянных балок это большого значения не имеет.
1.7. Определение требуемого момента сопротивления
Согласно СП 64.13330.2011 «Деревянные конструкции» п.6.9 расчет изгибаемых элементов, обеспеченных от потери устойчивости плоской формы деформирования, следует производить, исходя из следующего условия:
M/Wрасч ≤ Rи (или Rид.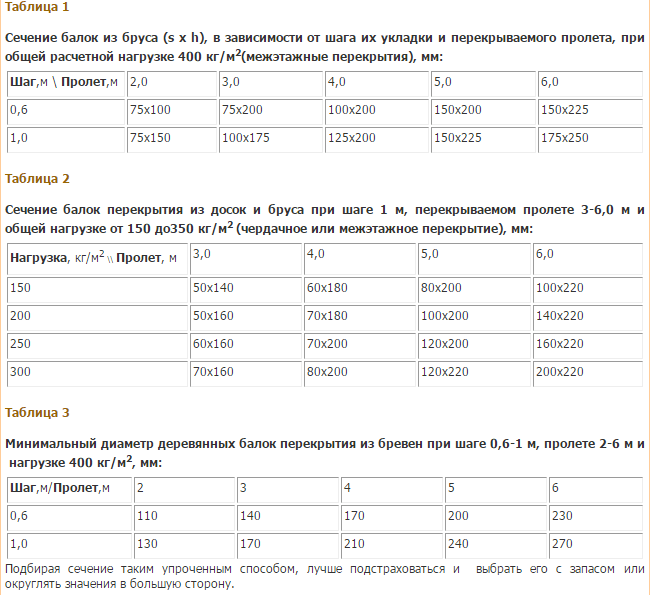 ш.) (533.1)
ш.) (533.1)
где М — расчетное значение изгибающего момента. В нашем случае (для балки постоянного сечения при действии равномерно распределенной нагрузки) достаточно проверить балку на действие максимального изгибающего момента. В общем случае при достаточно сложной комбинации различных нагрузок или для балок переменного сечения могут потребоваться проверки на прочность в нескольких сечениях. Для определения момента в этих сечениях и используется эпюра моментов.
Rи — расчетное сопротивление древесины изгибу. Определение расчетного сопротивления древесины в зависимости от различных факторов — отдельная большая тема. В данном случае ограничимся тем, что при использовании балок из цельной древесины — сосны 2 сорта расчетное сопротивление изгибу для балок перекрытия санузла может составлять Rи = 113.3 кгс/см2.
Rид.ш. — расчетное сопротивление для элементов из однонаправленного шпона, но так как в данном случае мы рассматриваем балку из цельной древесины, то возможные значения клееных элементов нас не интересуют
— расчетное сопротивление для элементов из однонаправленного шпона, но так как в данном случае мы рассматриваем балку из цельной древесины, то возможные значения клееных элементов нас не интересуют
Wрасч— расчетный момент сопротивления рассматриваемого поперечного сечения. Для элементов из цельной древесины Wрасч = Wнт, где Wнт — момент сопротивления рассматриваемого сечения с учетом возможных ослаблений — момент сопротивления нетто.
Так как для рассчитываемых балок не предусматривается никаких ослаблений в зоне максимального загружения (гвозди крепления досок перекрытия не в счет), то требуемый по расчету момент сопротивления поперечного сечения балки можно определить, преобразовав соответствующим образом формулу (533.1):
Wрасч ≥ М/Rи = 54582/113.3 = 481.73 см3
1.8. Определение геометрических параметров сечения
Если принять ширину балок 10 см, исходя из сортамента производимых в ближайших окрестностях лесоматериалов, то требуемую высоту поперечного сечения можно определить по формуле:
(147.4)
hтр = √6·481.73/10 = 17 см.
Исходя из все того же сортамента, высоту балок следует принять не менее 20 см. Также можно уменьшить шаг балок, например при шаге балок 0.45 м значение расчетного момента сопротивления составит не менее
Wрасч = 0.5·481.73/0.6 = 361.3 см3
и тогда минимально допустимая высота сечения
hтр = √6·361.3/10 = 14.72 см.
А значит можно принять высоту балок равной 15 см. Впрочем, возможны и другие варианты подхода, например, более точно учесть количество пролетов, перекрываемых досками, это позволит уменьшить значение нагрузки на 10-15%.
2. Определение прогиба
Так как для однопролетных балок с шарнирными опорами значение прогиба может стать определяющим, то я рекомендую определять прогиб сразу после определения параметров сечения.
При действии равномерно распределенной нагрузки на однопролетную балку с шарнирными опорами значение прогиба без учета влияния поперечных сил можно определить по следующей формуле:
f0 = 5ql4/(384EI)
где q — нормативное значение нагрузки.
Значения плоских нормативных нагрузок, необходимые для определения прогиба, мы уже определили при сборе нагрузок. Они составляют:
qнп = 171.6 кг/м2
qнв = 150 кг/м2
Соответственно с учетом шага балок 0.6 м и перераспределения опорных нагрузок линейная нормативная нагрузка составляет:
qнл = 0.6·1.25(171.6 + 150) = 241.2 кг/м (2.412 кг/см)
Е = 105 кгс/см2, модуль упругости древесины, принимаемый по СП 64.13330.2011 «Деревянные конструкции».
I = bh3/12 = 10·203/12 = 6666. 67 см4, — момент инерции рассматриваемого прямоугольного сечения балки.
67 см4, — момент инерции рассматриваемого прямоугольного сечения балки.
Тогда
f0 = 5·2.412·3784/(384·105·6666.67) = 0.962 см
При действии равномерно распределенной нагрузки на балку значение коэффициента с, учитывающего влияние поперечных сил на значение прогиба, составит согласно таблицы Е.3:
с = 15.4 + 3.8β (533.2)
Так как высота балки у нас постоянная величина, то β =1 = k и соответственно
с = 15.4 + 3.8 = 19.2
Тогда при высоте балки h = 0.2 м и пролете l = 3.78 м (h/l = 0.053) значение прогиба с учетом поперечных сил составит:
f = fo[1 + c(h/l)2]/k = 0.962[1 + 19.2·0.0532]/1 = 1.01 см
Предельно допустимое значение прогиба деревянных балок междуэтажного перекрытия согласно таблицы 19 СП 64. 13330.2011 «Деревянные конструкции» составляет fд = l/250 = 387/250 = 1.55 см.
13330.2011 «Деревянные конструкции» составляет fд = l/250 = 387/250 = 1.55 см.
Необходимые требования по максимально допустимому прогибу нами соблюдены, мы можем продолжать расчет.
1.9. Проверка по касательным напряжениям (прочность по скалыванию)
При изгибе в сечениях, поперечных и параллельных нейтральной оси балки, будут действовать касательные напряжения. В деревянных балках это может привести к скалыванию древесины вдоль волокон. поэтому касательные напряжения т не должны превышать расчетного сопротивления Rск скалыванию:
т = QS’бр/bрасIбр ≤ Rск (Rскд.ш.) (533.3)
где Q — значение поперечной силы в рассматриваемом поперечном сечении, определяемое по эпюре моментов. В нашем случае максимальные касательные напряжения будут действовать на опорах балки, Q = 557. 6 кг
6 кг
S’бр — статический момент брутто (т.е. без учета возможных ослаблений сечения) сдвигаемой (скалываемой) части сечения. Статический момент определяется относительно нейтральной оси балки.
bрас — расчетная ширина сечения рассматриваемого элемента конструкции. В данном случае у нас ширина балки равна bрас = 10 см.
Rск — расчетное сопротивление древесины скалыванию. Как и при определении расчетного сопротивления изгибу значение, определенное по таблице 3, следует дополнительно умножить на ряд коэффициентов, учитывающих различные факторы. Впрочем факторы у нас не изменились и потому согласно п.5.а) и определенным ранее коэффициентам расчетное сопротивление скалыванию составит:
Rск = 1.6·0.9·0.95 = 1.368 МПа (13.95 кгс/см2)
Iбр — момент инерции брутто, т. е. опять же определяемый без учета возможных ослаблений сечения. В данном случае момент инерции брутто совпадает с определенным ранее моментом инерции.
е. опять же определяемый без учета возможных ослаблений сечения. В данном случае момент инерции брутто совпадает с определенным ранее моментом инерции.
Впрочем, для балок прямоугольного сечения нет большой необходимости при подобных расчетах определять как статический момент полусечения, так и момент инерции. По той причине, что максимальные касательные напряжения действуют посредине высоты балки и составляют:
т = 1.5Q/F (270.3)
Тогда
т = 1.5·557.6/(10·20) = 4.182 кг/см2 < 13.95 кг/см2
Требование по прочности по скалыванию соблюдается, причем с 3-х кратным запасом.
На этом расчет деревянной балки постоянного сплошного сечения, устойчивость которой из плоскости изгиба обеспечена другими элементами конструкции, можно считать законченным. Во всяком случае никаких дополнительных требований Сводом Правил в таких случаях не предъявляется.
Тем не менее я рекомендую дополнительно проверить опорные участки балки
1.
 10. Проверка на прочность опорных участков балки
10. Проверка на прочность опорных участков балки
Любая балка в отличие от показанной на рисунке 219.2 модели имеет опорные участки. На этих опорных участках действуют нормальные напряжения в сечениях, параллельных нейтральной оси балки.
Распределение нормальных напряжений на этом участке зависит от множества различных факторов, в частности от угла поворота поперечного сечения балки на опоре, длины опорных участков и т.п.
Если для упрощения расчетов принять линейное изменение нормальных напряжений от максимума до 0, то примерное значение максимальных нормальных напряжений на опорных участках можно определить по следующей формуле:
σу = 2Q/(blоп) ≤ Rcм90 (533.4)
где Q — значение поперечной силы согласно эпюры «Q», как и прежде оно составляет Q = 557.6 кг;
b — ширина балки b = 10 см;
lоп — длина опорного участка, из конструктивных соображений примем lоп = 10 см;
2 — коэффициент учитывающий неравномерность распределения напряжений на опорном участке;
Rcм90 — расчетное сопротивление смятию поперек волокон. Согласно п.4.а) таблицы 3 и с учетом поправочных коэффициентов расчетное сопротивление смятию поперек волокон составит:
Rсм90 = 4·0.9·0.95 = 3.42 МПа (34.8 кгс/см2)
Тогда
2·557.6/(10·10) = 11.15 кг/см2 < 34.8 кг/см2
Как видим условие по прочности на опорных участках также соблюдается и снова с хорошим 3-х кратным запасом.
И теперь расчет балки перекрытия санузла можно действительно считать законченным.
Дополнительные проверки на прочность в местах действия сосредоточенных нагрузок здесь не требуются как минимум потому, что при принятой расчетной схеме сосредоточенные нагрузки отсутствуют. Да и рассматривать плоское напряженное состояние балки для определения максимальных напряжений при постоянном сплошном прямоугольном сечении балки и принятой схеме нагрузок и опор на мой взгляд также не требуется.
Расчет сечения деревянной балки перекрытия
Расчет деревянных несущих однопролетных
опорных балок
С целью упрощения расчетов, можно скачать файла в формате XLSX, см. ниже, для расчета деревянных несущих однопролетных опорных балок (из досок и брусьев).
Для расчета необходимо определиться с шагом балок (расстояние между осями балок) и уйти от так называемого явления «зыбкости» перекрытия. Шаг балок в разных источниках колеблется от 600 до 1040 мм (Линович Л.Е. Расчет и конструирование частей гражданских зданий, 1972 г.; Осипов Л.Г., Сербинович П.П., Красенский В.Е. Гражданские и промышленные здания, часть 1, 1957 г.), но рекомендуемым является шаг — не более 750 мм.
I. Расчет деревянной балки на прочность
Есть на пример междуэтажное деревянное перекрытие жилого дома. Расстояние между несущими стенами (пролет балки) — 5,0 м, расстояние между осями балок — 0,7 м.
Чертеж 1
Расчет:
1. Определить зону с которой будут собираться нагрузки на балку перекрытия. Она составляет половину расстояния между осями балок с одной и другой стороны от оси рассчитываемой балки. В нашем случае зона сбора нагрузки на балку составит:
0,35 + 0,35 = 0,7 м (см. Чертеж 1)
2. Определить нагрузку от перекрытия передающуюся на балку. Она состоит из собственного веса перекрытия и временной нагрузки на него.
Чертеж 2
Нужно найти вес 1 м2 каждого слоя (см. Чертеж 2):
— половая доска, толщ. — 0,05 м;
— звукоизоляция, толщ. — 0,1 м;
— вагонка доска, толщ. — 0,02 м.
Вес 1 м3 древесины для пород: сосна, ель, кедр, пихта (берем с запасом для класса условий эксплуатации 3 (влажный) из таблицы Г.1, свода правил «Деревянные конструкции») — 600 кг.
Вес 1 м3 звукоизоляции (в зависимости от плотности утеплителя, берем на пример URSA GEO M-15 с плотностью от 14 до 15 кг/м3) — 15 кг.
(600 х 0,05) + (15 х 0,1) + (600 х 0,02) = 43,5 кг/ м2
3. Определить вес 1 погонного метра балки. Для этого берем предполагаемое сечение несущей балки, на пример 0,12 х 0,2 (h) м, в таком случае вес 1 погонного метра балки составит:
600 х 0,12 х 0,2 = 14,4 кг/м.п.
4. Найти нормативную и расчетную нагрузки от 1 м2 перекрытия без учета балок перекрытия.
Нормативная нагрузка
Из свода правил «Нагрузки и воздействия»:
— временная нормативная нагрузка на междуэтажное перекрытие в жилых зданиях составляет — 1,5 кПа или 150 кг/м2;
— нормативная нагрузка от веса перегородок составляет — 0,75 кПа или 75 кг/м2 ;
— нормативные значения нагрузок на ригели и плиты перекрытий от веса временных перегородок следует принимать в зависимости от их конструкции, расположения и характера опирания на перекрытия и стены. Указанные нагрузки допускается учитывать как равномерно распределенные добавочные нагрузки, принимая их нормативные значения на основании расчета для предполагаемых схем размещения перегородок, но не менее 0,5 кПа или — 50 кг/м2). Лучше учесть вес предполагаемых к установке перегородок — 75 кг/м2.
Нормативная нагрузка от 1 м2 перекрытия без учета балок перекрытия составит:
43,5 + 150 + 75 = 268,5 кг/м2
Расчетная нагрузка
Из свода правил «Нагрузки и воздействия»:
— коэффициент надежности по нагрузке для веса строительных конструкций для: бетонные (со средней плотностью свыше 1600 кг/м), железобетонные, каменные, армокаменные, деревянные — 1,1 (применяем для перекрытия);
— временная нормативная нагрузка на междуэтажное перекрытие в жилых зданиях составляет — 1,5 кПа или 150 кг/м2;
— нормативные значения нагрузок на ригели и плиты перекрытий (в нашем случае деревянное перекрытие) от веса временных перегородок следует принимать в зависимости от их конструкции, расположения и характера опирания на перекрытия и стены. Указанные нагрузки допускается учитывать как равномерно распределенные добавочные нагрузки, принимая их нормативные значения на основании расчета для предполагаемых схем размещения перегородок, но не менее 0,5 кПа. 1,3 — при полном нормативном значении менее 2,0 кПа; если нагрузка на перекрытие 2,0 кПа и более, то 1,2 — при полном нормативном значении нагрузки;
— нормативные значения нагрузок на ригели и плиты перекрытий от веса временных перегородок следует принимать в зависимости от их конструкции, расположения и характера опирания на перекрытия и стены. Указанные нагрузки допускается учитывать как равномерно распределенные добавочные нагрузки, принимая их нормативные значения на основании расчета для предполагаемых схем размещения перегородок, но не менее 0,5 кПа или — 50 кг/м2). Также лучше учесть вес предполагаемых к установке перегородок — 75 кг/м2;
— нормативные значения нагрузок на ригели и плиты перекрытий от веса временных перегородок следует принимать в зависимости от их конструкции, расположения и характера опирания на перекрытия и стены. Указанные нагрузки допускается учитывать как равномерно распределенные добавочные нагрузки, принимая их нормативные значения на основании расчета для предполагаемых схем размещения перегородок, но не менее 0,5 кПа. 1,3 — при полном нормативном значении менее 2,0 кПа; если нагрузка на перекрытие 2,0 кПа и более, то 1,2 — при полном нормативном значении нагрузки.
Расчетная нагрузка от 1 м2 перекрытия без учета балок перекрытия составит:
(43,5 х 1,1) + (150 х 1,3) + (75 х 1,3) = 340,35 кг/м2
5. Найти нормативную и расчетную нагрузки от 1 м2 перекрытия с учетом балок перекрытия при ширине сбора нагрузки = 0,7 м.
Нормативная нагрузка
268,5 х 0,7 + 14,4 = 202,35 кг/п.м.
Расчетная нагрузка
Из свода правил «Нагрузки и воздействия»:
— коэффициент надежности по нагрузке для веса строительных конструкций для: бетонные (со средней плотностью свыше 1600 кг/м), железобетонные, каменные, армокаменные, деревянные — 1,1 (применяем для балки перекрытия);
(340,35 х 0,7) + (14,4 х 1,1) = 254,09 кг/п.м.
6. Определить изгибающий момент балки:
где,
M — изгибающий момент балки, в кгм;
q — расчетная нагрузка на 1 п.м. балки;
l — пролет балки.
(254,09 х 25) / 8 = 794,0 кгм
7. Определить сечение балки (расчет на прочность по расчетным нагрузкам)
Из свода правил «Деревянные конструкции»:
— расчетное сопротивление древесины на изгиб — 130 кгс/м2
Найти момент сопротивления деревянной балки в см3, для этого переводим 794,0 кгм (изгибающий момент балки) в кгсм.
794,0 х 100 = 79400 кгсм
Далее находим сам момент сопротивления — W
79400 / 130 = 610,8 см3
Далее по таблицам 1 (Моменты сопротивления (W) и инерции (J) досок и брусьев) или 2 (Моменты сопротивления (W) и инерции (J) бревен) исходя из полученного расчетом момента сопротивления 610,8 см3 подобрать сечение балки исходя из принятой до начала расчета высоты балки — 20 см.
Из таблицы 1 для досок и брусьев подходит балка 10 х 20 с моментом сопротивления 667, но лучше взять с запасом следующего с сечения 12 х 20, как и предполагалось. Из таблицы 2 для бревен подходит балка диаметром 20 см с моментом сопротивления 785.
Таблица 1. Моменты сопротивления (W) и инерции (J) досок и брусьев
Таблица 2. Моменты сопротивления (W) и инерции (J) бревен
Применять подобранные балки после расчета на прочность нельзя, т.к. их необходимо проверить еще и на прогиб.
II. Расчет деревянной балки на прогиб
Расчет деформации при изгибе выполняется по нормативным нагрузкам.
1. Перевести полученную ранее нормативную нагрузку на 1 п.м. балки при ширине сбора нагрузки 0,7 м — 202,35 кг/п.м в кгс/см
202,35 / 100 = 2,024 кгс/см
и пролет балки — 5 м в см
5 х 100 = 500 см
2. Вычислить прогиб балки
где
f — прогиб балки, в см;
q — нормативная нагрузка на 1 п.м. балки;
l — пролет балки;
E — модуль упругости древесины вдоль волокон — 100000;
J — момент инерции балки из таблицы 1 (в нашем случае берем значение 8000 для подобранной балки 12 х 20 (h)).
(5 / 384) х ((2,024 х 5004) / (100000 х 8000)) = 2,06 см
3. Найти предельный прогиб для нашей балки пролетом 500 см
Из старого свода правил «Деревянные конструкции» (не действующий) см. табл. 3:
— предельный прогиб в долях пролета для балок междуэтажных перекрытий — 1/250.
Таблица 3. Предельные прогибы в долях пролета
Сейчас есть эстетическо-психологические требования к прогибам деревянных балок в своде правил «Нагрузки и воздействия», но они менее требовательны, так что лучше пользоваться данной таблицей.
500 / 250 = 2 см (предельный прогиб для нашей балки)
4. Сравнить полученный предельный прогиб балки с предельным расчетным прогибом.
У нас прогиб получился больше 2 см, а именно — 2,06 см, значит увеличиваем сечение балки до 15 х 20.
Снова находим момент инерции, только в формулу уже подставляем из таблицы момент инерции для балки, сечением 15 х 20 (h) — 10000.
Также подствляем в формулу нормативную нагрузку,
переведенную в кгс/см с учетом веса балки 0,15 х 0,2:
Вес балки — 600 х 0,15 х 0,2 = 18,0 кг/м.п.
Нормативная нагрузка — 268,5 х 0,7 + 18,0 = 205,95 кг/п.м.
Перевод нормативной нагрузки из кг/п.м в кгс/см – 205,95 / 100 = 2,06 кгс/см.
Подставляем полученные данные в формулу
(5 / 384) х ((2,06 х 5004) / (100000 х 10000)) = 1,68 см
Это меньше допустимого прогиба — 2,0, значит берем балку длиной 5 м, сечением 15 х 20.
Таким образом, после выполненных расчетов деревянной балки на прочность и на прогиб от воздействия нагрузок, применяем в конструкции перекрытия деревянные балки длиной 5 м, сечением 15 х 20 (h), с шагом между осями балок 0,7 м.
Более сложные расчеты можно заказать в лицензированной организации.
Онлайн калькулятор для расчета желебобетонных балок перекрытия дома
ДалееПересчитать
Назначение калькулятора
Калькулятор для расчёта железобетонных балок перекрытий предназначен для определения габаритов, конкретного типа и марки бетона, количества и сечения арматуры, требующихся для достижения балкой максимального показателя выдерживаемой нагрузки.
Соответственно СНиП 2.03.01-84 «Бетонные и железобетонные конструкции» габариты железобетонных балок перекрытия и их устройство подсчитываются по дальнейшим принципам:
- Минимальная высота балки перекрытия должна составлять не меньше 1/20 части длины перекрываемого проёма. К примеру при длине проёма в 5 м минимальная высота балок должна составлять 25 см;
- Ширина железобетонной балки устанавливается по соотношению высоты к ширине в коэффициентах 7:5;
- Армировка балки состоит минимум из 4 арматур – по два прута снизу и сверху. Применяемая арматура должна составлять не меньше 12 мм в диаметре. Нижнюю часть балки можно армировать прутами большего сечения, чем верхнюю;
- Железобетонные балки перекрытия бетонируются без перерывов заливки, одной порцией бетонной смеси, чтобы не было расслоения бетона.
Дистанцию между центрами укладываемых балок определяют длиной блоков и установленной шириной балок. К примеру, длина блока составляет 0,60 м, а ширина балки 0,15. Дистанция между центрами балок будет равна – 0,60+0,15=0,75 м.
Принцип работы
Согласно ГОСТ 26519-85 «Конструкции железобетонные заглублённых помещений с перекрытием балочного типа. Технические условия» формула расчёта полезной нагрузки железобетонных балок перекрытия складывается из следующих характеристик:
- Нормативно-эксплуатационная нагрузка на балки перекрытия с определённым коэффициентным запасом. Для жилых зданий данный показатель нагрузки составляет 151 кг на м2, а коэффициентный запас равен 1,3. Получаемая нагрузка – 151*1,3=196,3 кг/м2;
- Нагрузка от общей массы блоков, которыми закладываются промежутки между балками. Блоки из лёгких материалов, к примеру из пенобетона или газобетона, показатель плотности которых D-500, а толщина 20 см будут нести нагрузку – 500*0,2=100 кг/м2;
- Испытываемая нагрузка от массы армированного каркаса и последующей стяжки. Вес стяжки с толщиной слоя 5 см и показателем плотности 2000 кг на м3 будет образовывать следующую нагрузку – 2000*0,05=100 кг/м2 (масса армировки добавлена в плотность бетонной смеси).
Показатель полезной нагрузки железобетонной балки перекрытия составляется из суммы всех трёх перечисленных показателей – 196,3+100+100=396,3 кг/м2.
Расчет нагрузки деревянной балки онлайн для минимальной прочности и прогиба перекрытия
Задача расчета балки для деревянного перекрытия по прогибу и прочности сводится к тому, чтобы найти поперечное сечение деревянных балок и определить их шаг, чтобы перекрытие было достаточно прочным и было способно выдерживать определенную нагрузку. И для того, чтобы не возникали чрезмерные прогибы, которые могут создавать существенный дискомфорт тем, кто будет ходить по такому перекрытию.
Для этого мы сделали данный калькулятор деревянного перекрытия на прогиб и прочность для деревянной балки.
Порядок работы:
1. Укажите длину пролета балки
2. Укажите шаг балок
3. Укажите расчетную нагрузку на балку (посчитать можно здесь)
4. Укажите сорт дерева (для расчета по прочности)
5. Укажите либо отношение высоты к ширине (h/b), либо напрямую задать ширину с последующим расчетом высоты
6. Нажать на кнопку «Расчет»
В результате вы получите подбор минимального сечения по прочности и прогибу деревянной балки, и на основании этих значений подбор окончательного варианта сечения и площадь для рационального использования сечения балки.
Для информации:
— принято считать, что сопротивление дерева на изгиб: для 1-ого сорта — 9 МПа, для 2-ого сорта — 8.34 МПа и для 3-его сорта — 5.56 МПа. Это следует из СП 64.13330.2017 «Деревянные конструкции» при коэффициентах Mв=0.9 (нормальная эксплуатация), Mт=0.8 (температура до 50 градусов), Мсс=0.9 (срок службы 75 лет), Мдл=0.66 (совместное действие постоянной и кратковременной нагрузок).
Если онлайн калькулятор расчета деревянной балки на прочность и прогиб оказался Вам полезен – не забывайте делиться им с друзьями и коллегами ссылкой в соц.сети, а также посмотреть другие строительные калькуляторы онлайн, они простые но здорово облегчают жизнь строителям и тем кто решил сам строить свой дом с нуля.
Расчет на прочность | ПроСопромат.ру
Задача 1
В некотором сечении балки прямоугольного сечения 20×30см М=28 кНм, Q=19 кН.
Требуется:
а) определить нормальное и касательное напряжения в заданной точке К, отстоящей от нейтральной оси на расстоянии 11 см,
б) проверить прочность деревянной балки, если [σ]=10 МПа, [τ]=3 МПа.
Решение
а) Для определения σ(К), τ(К) и maxσ,maxτ потребуется знать величины осевого момента инерции всего сечения IН.О., осевого момента сопротивления WН.О., статического момента отсечённой части и статического момента половины сечения Smax:
Тогда:
б) Проверка прочности:
— по условию прочности нормальных напряжений:
— по условию прочности касательных напряжений:
Задача 2
В некотором сечении балки М=10кНм, Q=40кН. Поперечное сечение – треугольное. Найти нормальное и касательное напряжения в точке, отстоящей от нейтральной оси на расстоянии 15 см.
где
Тогда
где:
Тогда
Задача 3
Подобрать сечение деревянной балки в двух вариантах: круглое и прямоугольное (при h/b=2), если [σ]=10 МПа, [τ]=3 МПа, и сравнить их по расходу материала.
Задаёмся направлениями опорных реакций А и В и составляем уравнения статики:
(1) ∑М(В) = F·8 – М – А·6 + (q·6)·3 =0,
откуда
(2) ∑М(А) = F·2 – М + В·6 — (q·6)·3 =0,
откуда
Iучасток
∑М(С) = М(z1) +F·z1=0,
ММ(z1) = —F·z1= — 30 ·z1 —
– уравнение прямой.
При z1 = 0: М = 0,
z1 = 2: М =- 60 кНм.
∑у= — F — Q(z1) = 0,
Q(z1) = — F = -30 кН – постоянная функция.
II участок
откуда
— уравнение параболы.
При z2=0: М = 0,
z2=3м: М = 30 · 3 – 5 · 32 = 90 — 45 = 45кНм,
z2=6м: М = 30 · 6 – 5 · 62 = 180 — 180 = 0.
∑у= Q(z2) — q·z2 + B= 0,
Q(z2) = q·z2 — B= 10·z2 – 30 – уравнение прямой,
при z2 = 0: Q = -30,
z2 = 6м: Q = 10·6 – 30 = 30.
Определение аналитического максимума изгибающего момента второго участка:
из условиянаходим :
И тогда
Заметим, что скачок в эп.М расположен там, где приложен сосредоточенный момент М = 60кНм и равен этому моменту, а скачок в эп.Q – под сосредоточенной силой А = 60 кН.
Подбор сечения балок производится из условия прочности по нормальным напряжениям, куда следует подставлять наибольший по абсолютной величине изгибающий момент из эпюры М.
В данном случае максимальный момент по модулю М = 60кНм
откуда: :
а) сечение круглой формы d=?
б) сечение прямоугольной формы при h/b = 2:
тогда
Размеры сечения, определенные из условия прочности по нормальным напряжениям, должны удовлетворять также условию прочности по касательным напряжениям:
Для простых форм сечений известны компактные выражения наибольшего касательного напряжения:
— для круглого сечения
— для прямоугольного сечения
Воспользуемся этими формулами. Тогда
— для балки круглого сечения при :
— для балки прямоугольного сечения
Чтобы выяснить, какое сечение требует меньшего расхода материала, достаточно сравнить величины площадей поперечных сечений:
Апрямоугольного = 865,3см2 < Акруглого = 1218,6см2, следовательно, балка прямоугольного сечения в этом смысле выгоднее, чем круглого.
Задача 4
Подобрать двутавровое сечение стальной балки, если [σ]=160МПа, [τ]=80МПа.
Задаёмся направлениями опорных реакций А и В и составляем два уравнения статики для их определения:
(1) ∑М(А) = – М1– F ·2 — (q·8)·4 + М2 + В·6 =0,
откуда
(2) ∑М(В) = – М1– А · 6 + F · 4 + (q·8)·2 + М2 =0,
откуда
Проверка:
∑у = А – F – q · 8 + В = 104 – 80 – 20 · 8 +136 = 240 – 240 ≡ 0.
∑М(С) = М(z1) — М1=0,
М(z1) = М1= 40 кНм – постоянная функция.
∑у= — Q(z1) = 0,
Q(z1) = 0.
II участок
— парабола.
Приz2=0: М = 40 кНм,
z2=1м: М = 40 + 104 – 10=134кНм,
z2=2м: М = 40+ 104 · 2 – 10 · 22 = 208 кНм.
∑у=А — q·z2 — Q(z2) = 0,
Q(z2) =А— q·z2 = 104 – 20·z2 – уравнение прямой,
при z2 = 0: Q = 104кН,
z2 = 6м: Q = 104 – 40 = 64кН.
III участок
— парабола.
Приz3=0: М = 24+40=-16 кНм,
z3=2м: М = 24 + 136·2 — 10 (2+2)2 = 24 + 272 – 160 = 136кНм,
z3=4м: М = 24 + 136·4 – 10 (2+4)2 = 24 + 544 – 360 = 208 кНм.
∑у=В — q(2+z3 ) + Q(z3) = 0,
Q(z3) =- В + q(2+z3 ) = -136 + 20 (2+z3 ) – уравнение прямой,
при z3 = 0: Q = -136 + 40 = — 94кН,
z3 = 4м: Q = — 136 + 20 (2+4) = — 136 + 120 = — 16кН.
IV участок
— парабола.
z4=0: М = 0кНм,
z4=1м: М = – 10кНм,
z4=2м: М = — 40кНм.
∑у=- q·z4 + Q(z4) = 0,
Q(z4) =q·z4 = 20·z4 – уравнение прямой.
Приz4 = 0: Q = 0,
z4 = 2м: Q = 40кН.
Проверяем скачки в эпюрах:
а) В эпюре М скачок на правой опоре величиной 24кНм (от 16 до 40) равен сосредоточенному моменту М2=24, приложенному в этом месте.
б) В эпюре Q три скачка:
первый из них на левой опоре соответствует сосредоточенной реакции А=104кН,
второй – под силой F=80кН и равен ей (64+16=80кН),
третий – на правой опоре и соответствует правой опорной реакции 136кН (94+40=136 кН)
Наконец, проектируем двутавровое сечение.
Подбор его размеров производится из условия прочности по нормальным напряжениям :
В сортаменте двутавровых профилей профиля с точно таким моментом сопротивления Wх нет. Есть № 40а с Wх=1190 см3 и № 45а с Wх=1430 см3
Попробуем меньший из них. Если принять двутавр № 40а, у которого Wх=1190 см3 , то наибольшее напряжение в опасном сечении будет:
и перенапряжение составитчто превышает рекомендуемую величину отклонения, равную 5%.
Поэтому приходится принимать ближайший больший размер двутавра, а именно №45а, у которого Wх=1430 см3. В этом случае балка будет работать с недонапряжением:
что меньше [σ]=160МПа на
Итак, принимается двутавр №45а, у которого: Wх=1430 см3, Iх=32240см4, Iх: Sх=38,6см, d=11,5мм.
Далее необходима проверка прочности по касательным напряжениям с помощью условия прочности :
Это условие прочности выполняется, даже с избыточным запасом.
Задача 5
Подобрать сечение балки, рассмотрев шесть вариантов форм и три вида материалов (древесина, чугун, сталь).
Решение
1.Определение опорных реакций
∑М(А) = F · 2 + М1 — М2— q·6·7 + В · 8 =0,∑М(В) = F · 10 + М1— М2 – А · 8 + q·6·1 =0,Проверка:
∑у = – 20 – 40 ·6 +50+210 = — 260 + 260 ≡ 0.
2.Построение эпюр изгибающих моментов и поперечных сил.
I участок
∑М(С) = М(z1) + F·z1=0,
М(z1) = — F·z1= -20·z1.
При z1=0: М = 0,
z1=2м: М = – 40кНм,
∑у= — F— Q(z1) = 0,
Q(z1) = — 20кН.
II участок
z2=0: М = — 20 – 40 = -60 кНм,
z2=4м: М = 200 — 20 – 120 = 200 — 140 = 60кНм.
∑у=- F + А — Q(z2) = 0,
Q =- F + А= -20+50=30кН.
III участок
— парабола.
Приz3=0: М = — 20·4= — 80 кНм,
z3=2м: М = 210·2 — 20·(2+2)2 = 420 – 320 = 100кНм,
z3=4м: М = 210·4 – 20 · (2+4)2 = 840 – 720 = 120кНм.
∑у= Q(z3) + В — q·(2+z3) = 0,
Q(z3) = — В + q·(2+z3) = — 210 + 40·(2+z3) – уравнение прямой.
Приz3 = 0: Q = -130кН,
z3 = 4м: Q = 30кН.
Q(z0) = — 210 + 40·(2+z0) = 0,
— 210 + 80 + 40·z0 = 0,
40·z0 = 130,
z0 =3,25м,
IV участок
парабола.
Приz4=0: М = 0 кНм,
z4=1м: М = – 20кНм,
z4=2м: М = — 80кНм.
∑у=- q·z4 + Q(z4) = 0,
Q(z4) =q·z4 = 40·z4 – уравнение прямой,
z4 = 0: Q = 0,
z4 = 2м: Q = 80кН.
3. Подбор сечений (опасное сечение по σ: |maxМ|=131,25кНм,
опасное сечение по τ: |maxQ|=130кН).
Вариант 1. Деревянное прямоугольное ([σ]=15МПа, [τ]=3МПа)
Принимаем: В=0,24м,
Н=0,48м.
Проверяем по τ:
Вариант 2. Деревянное круглое
Принимаем d=0,45м,
Проверяем по τ:
Вариант 3. Чугун : ([σР]=30МПа, [σс]=120МПа, [τ]=15МПа)
Принимаем b=0,19м, тогда h=0,38м, d=0,076м.
Проверка по τ:
b(у)= b — d= 0,19 — 0,076 = 0,114м
Вариант 4. Сталь, двутавр : ([σ]=160МПа, [τ]=80МПа).
по сортаменту Wх=953см3. Это №40: Ix=19062см4, Sх=545см3, d=0,83см.
Проверка по τ:
Вариант 5. Сталь, круглая труба
Принимаем D=0,22м → d = 0,6·D =0,132м.
Проверка по τ:
Вариант 6. Сталь, прямоугольная труба
b1= b — 2t = b — 2·0,1b = 0,8b,
h1= h — 2t = 0,8h,
Принимаем b=0,13м, h=0,26м.
Проверка по τ:
Кстати: какое из сечений стальной балки выгодней по расходу материала?
Двутавр — А = 72,6см2 = 72,6·10-4 = 0,00726м2,
круглая труба –
прямоугольная труба —
Самый лёгкий: двутавр → самый выгодный с точки зрения изгиба.
Расчет балки на изгиб — Favorit-TK.ru
Рассчитывать балку на изгиб можно несколькими вариантами:1. Расчет максимальной нагрузки, которую она выдержит
2. Подбор сечения этой балки
3. Расчет по максимальным допустимым напряжениям (для проверки)
Давайте рассмотрим общий принцип подбора сечения балки на двух опорах загруженной равномерно распределенной нагрузкой или сосредоточенной силой.
Для начала, вам необходимо будет найти точку (сечение), в которой будет максимальный момент. Это зависит от опирания балки или же ее заделки. Снизу приведены эпюры изгибающих моментов для схем, которые встречаются чаще всего.
После нахождения изгибающего момента мы должны найти момент сопротивления Wx этого сечения по формуле приведенной в таблице:
Далее, при делении максимального изгибающего момента на момент сопротивления в данном сечении, мы получаем максимальное напряжение в балке и это напряжение мы должны сравнить с напряжением, которое вообще сможет выдержать наша балка из заданного материала.
Для пластичных материалов (сталь, алюминий и т.п.) максимальное напряжение будет равно пределу текучести материала, а для хрупких (чугун) – пределу прочности. Предел текучести и предел прочности мы можем найти по таблицам ниже.
Давайте рассмотрим пару примеров:
1. Вы хотите проверить, выдержит ли вас двутавр №10 (сталь Ст3сп5) длиной 2 метра жестко заделанного в стену, если вы на нем повисните. Ваша масса пусть будет 90 кг.
Для начала нам необходимо выбрать расчетную схему.
На данной схеме видно, что максимальный момент будет в заделке, а поскольку наш двутавр имеет одинаковое сечение по всей длине, то и максимальное напряжение будет в заделке.
Давайте найдем его:
P = m * g = 90 * 10 = 900 Н = 0.9 кН
М = P * l = 0.9 кН * 2 м = 1.8 кН*м
По таблице сортамента двутавров находим момент сопротивления двутавра №10.
Он будет равен 39.7 см3. Переведем в кубические метры и получим 0.0000397 м3.
Далее по формуле находим максимальные напряжения, которые у нас возникают в балке.
б = М / W = 1.8 кН/м / 0.0000397 м3 = 45340 кН/м2 = 45.34 МПа
После того, как мы нашли максимальное напряжение, которое возникает в балке, то мы его может сравнить с максимально допустимым напряжением равным пределу текучести стали Ст3сп5 – 245 МПа.
45.34 МПа < 245 МПа – верно, значит данный двутавр выдержит массу 90 кг.
2. Поскольку у нас получился довольно-таки большой запас, то решим вторую задачу, в которой найдем максимально возможную массу, которую выдержит все тот же двутавр №10 длиной 2 метра.
Если мы хотим найти максимальную массу, то значения предела текучести и напряжения, которое будет возникать в балке, мы должны приравнять (б=245 Мпа = 245 000 кН*м2).
Далее по формуле б = М / W, находим максимальный момент.
М = б * W = 245 000 * 0.0000397 = 9.73 кН * м
Тогда по формуле M = P * L найдем P:
P = 9,73 кН/м / 2м = 4,87 кН = 487 кг
Итак, максимальная масса, которую выдержит двутавр №10 – 487 кг. Число это грубое, поскольку для простоты расчета мы не учитывали различные коэффициенты запаса, поэтому, чтобы подстраховаться, возьмите некий двукратный запас по прочности.
Балки перекрытия в деревянном доме Расчет и выбор сечения.
Для сооружения прочного и надежного перекрытия выполняются расчеты для определения параметров конструкции. Цель расчета — определение оптимального соотношения размера сечения балок и расстояния между ними в конструкции. Это делается, чтобы избежать «играющих» перекрытий.И так, цель поставлена: мы не хотим, чтобы в нашем доме при ходьбе, например, по второму этажу трясся весь дом. Выход прост – нужно правильно определить, какой пролет, каким сечением доски (балки) можно перекрывать.
Что такое балка?
Балка – линейный элемент несущей конструкции, опирающийся на оба конца и работающий преимущественно на изгиб. Материал изготовления у них может быть как дерево, так и метал. Металлические балки применяются при строительстве каменных домов.
Бывает несколько видов балок:
• Круглые (1) и овальные (2). Изготавливаются из бревна, предварительно очищают бревно от коры или используют оцилиндрованное бревно. Такие балки используются редко в каркасном домостроении, т.к. бревно не подвергается камерной сушке и на открытой местности, в естественных условиях, его не высушить для нужного значения степени влажности;
• Квадратные. Чаще всего используется брус (3). Его также не рекомендуют использовать в каркасном домостроении, по той же причине что и бревна-его не просушить, а сырое или бревно естественной влажности будет гнить;
• Прямоугольная (4 – составная балка (из доски), 5 — LVL брус,7 — доска), это самая распространённая форма. Такие типы прямоугольной балки можно просушить в камере, а это значит, что такие элементы не будут гнить, и им не нужна усадка.
• Двутавровые (6), такие балки называются так из-за их формы. Такая балка считается достаточно прочной, но ее изготовление дорогое.
Важно чтобы балки перекрытий были: сухие – допускается влажность, не превышающая 14%; сорт использованной доски должен быть А, В; обработанные специальным составом – огнебиозащитой, для того чтобы дерево не гнило и была повышенная огнестойкость.
Первое что мы должны понять — что при определении параметров конструкции учитывается: длина перекрытия (которая приравнивается к ширине перекрываемого пролета), сечение доски (балки), расстояние между балками (шаг балок) и величина нагрузки, оказываемой на них.
Теперь о каждом пункте подробнее.
1. Длина перекрытия.
Длина перекрытия – расстояние между несущими элементами (стена, опора), на которые будут опираться балки.
Длину перекрытий нам нужно знать для того, чтобы правильно выбрать длину балки ведь она берется с учетом запаса для опирания на стены.
Глубина опирания на стены берется на основании того из какого материала построен дом. Для кирпича или блочных стен: опирание 10-12 см при условии использования доски и 15 см при использовании бруса. Для изготовления перекрытия в бревенчатом (или брусовом) доме балки устанавливаются в зарубки в стенах на глубину не менее 7 см. В каркасном доме опирание балок не менее 10 см.
Вычислить ширину пролета, которую вам нужно перекрыть, не сложно, это можно сделать обычной рулеткой. Главное знать максимальную длину пролета, которую перекрывает балка с определенным сечением. Чтобы не запоминать кучу цифр можно воспользоваться специальными онлайн — калькуляторами для расчетов.
|
Давайте рассмотрим на примере наших сечений: Мы используем доску сечением 45х195 мм, такое сечение доски позволит перекрыть пролет до 4 метров. Если поменять сечение и взять доску 45х145 мм, то такой доской можно перекрыть пролет только до 2,5 метров. Пролет до 5 метров можно перекрыть брусом сечением 200х200 мм, но использовать его мы вам не рекомендуем, лучше взять балку составного сечения (две доски сечением 45х145мм и скрепить их металлозубчатой пластиной (МЗП)). Получается, что обычной доской можно перекрыть пролет только до 4 метров, если хочется пролет больше, то нужна тяжелая артиллерия в виде ферм, LVL бруса или двутавровых балок. Мы не будем останавливаться на LVL брусе или двутавровых балках все характеристики задает завод изготовитель, поэтому что-либо о них сказать очень сложно. Мы используем фермы на металлозубчатых (гвоздевые) пластинах — МЗП. Такими фермами можно перекрыть любые пролеты. Ограничения вводит транспорт для перевозки таких ферм, длинна самого длинного транспорта составляет 12 метров. В таком случае, если нужна ферма длиннее 12 метров, ее делают составной. |
Мы изготавливаем фермы 2 видов: сдвоенная и с параллельными поясами
2. Сечение балок деревянного перекрытия
Зная длину балок деревянного перекрытия (А) и определив общую расчетную нагрузку можно определить необходимое их сечение (или диаметр) и шаг укладки, которые связаны между собой. Считается, что лучшим является прямоугольное сечение балки деревянного перекрытия, с соотношением высоты (H) и ширины (В) как 1,4:1.
Чаще всего высота и шаг балок зависит от выбранной толщины утеплителя, для того чтобы не оставлять обрезков, столь дорогостоящего материала. Но это не обязательно. Стандартный шаг балок считается от 0,6 м — 1 м.
Также шаг балок зависит от нагрузки на перекрытия. Например, шаг балок в чердачных перекрытиях (неэксплуатиромого чердака) будет отличаться от шага балок в межэтажных и цокольных перекрытиях, но о нагрузках позже.
Ниже сводные таблицы, где представлено, какие пролеты каким сечением доски перекрываются и какой при этом должен у этой балки быть шаг.
Таблица расчета балок межэтажных перекрытий и нежилого чердака. Расчеты для сухих строганных пиломатериалов хвойных пород сортностью не ниже 2го сорта
Если балки будут крепиться с помощью крепежных элементов (уголки, кронштейны, хомуты), то за длину деревянных балок принимают ширину пролета
3. Расчет нагрузки на перекрытия.
Такой расчет производят в момент проектирования. Он включает в себя учет веса самих перекрытий и всё, что будет находиться внутри комнаты, с учетом тех, кто будет там передвигаться.Стандартной временной равномерно распределенной нагрузкой принято считать 2,4кПа. Это значит, что в расчете учитывался вес:
- нагрузка от собственного веса элементов перекрытия (конструкций перекрытия, утеплителя, чернового и чистового пола, подшивки, а также отделки потолка, если это межэтажное перекрытие). При отсутствии стяжки, это нагрузка ок. 50кг на 1м2.
- временной нагрузки это нагрузки от всего остального: мебели, людей, домашних любимцев и т.д. эта нагрузка и есть 2,4кПа, т.е. ок.250кг на 1м2.
При использовании чердачного пространства для устройства мансарды, необходимо учесть вес полов, перегородок, мебели. В этом случае общую расчетную нагрузку необходимо увеличить до 350-400 кг/м2.
Более подробные правила расчета перекрытий можно найти в СП 20.13330.2016 «Нагрузки и воздействия».
Вычислитель момента инерции Т-образного сечения
Вычислитель момента инерции Т-образного сечения для второго момента площади, модуля сечения, радиуса инерции, площади поперечного сечения и расчета центроида балки Т-образного сечения. 3
Примечание: используйте точку «.»как десятичный разделитель.
Второй момент области: The способность поперечного сечения противостоять изгибу.
Радиус вращения (Площадь): The расстояние от оси, на котором площадь тела может считаться равной сосредоточена, а площадь второго момента этой конфигурации равна площадь второго момента фактического тела относительно той же оси.
Модуль упругости сечения: Момент инерция площади поперечного сечения элемента конструкции, деленной на расстояние от центра тяжести до самой дальней точки разреза; а мера прочности на изгиб балки.
Расчет центроида сечения балки
размер шрифта: 15 пикселей;}
]]>
Расчет центроидов: простое руководство
Центроид или центр масс секций балки полезен для анализа балки, когда момент инерции требуется для таких расчетов, как напряжение сдвига / изгиба и прогиб.
Секции балок обычно состоят из одной или нескольких форм. Итак, чтобы найти центр тяжести всей площади сечения балки, сначала необходимо разбить ее на соответствующие сегменты. После этого необходимо учитывать площадь и центроид каждого отдельного сегмента, чтобы найти центроид всей секции.
Или попробуйте наш бесплатный калькулятор центроидов:
Калькулятор свободного момента инерции
Рассмотрим сечение двутавровой балки, показанное ниже. Чтобы вычислить вертикальный центроид (в направлении y), его можно разделить на 3 сегмента, как показано на рисунке:
Теперь нам просто нужно использовать формулу для вычисления вертикального (y) центроида многосегментной формы:
Базовую или опорную линию возьмем снизу секции балки.{2} \\
{y} _ {3} & = \ tfrac {38} {2} = 19 \ text {mm} \\\\
\ end {align}
[math]
В случае, если поперечное сечение состоит из двух материалов или композитного материала, тогда один из материалов необходимо умножить на модульное соотношение, чтобы уравнение в целом сечение стало однородным.
[математика]
n = \ frac {E_ {1}} {E_ {2}}
[математика]
Обычно E 1 — это модуль упругости не преобладающего материала, а E 2 — модуль упругости преобладающего материала, хотя какой бы порядок ни был предпочтительным, не повлияет на решение центроида.С поправкой на второй материал формула центроида становится следующей.
[математика]
\ bar {y} = \ frac {\ sum {A} _ {i} {y} _ {i} + \ sum {n} {A} _ {i} {y} _ {i} } {\ sum {A} _ {i} + \ sum {n} {A} _ {i}}
[математика]
Конечно, ручное вычисление момента инерции не требуется с использованием нашего фантастического калькулятора центроидов, чтобы найти центроиды по вертикали (y) и горизонтали (x) секций балки.
Калькулятор свободного момента инерции
Чтобы получить более полный список разделов и функций, вы можете попробовать наш Конструктор разделов
Посетите следующий шаг: Как рассчитать момент инерции секции балки.
Как рассчитать момент инерции балки?
размер шрифта: 15 пикселей;}
]]>
Как рассчитать момент инерции секции балки
(Второй момент площади)
Прежде чем мы найдем момент инерции (или второй момент площади) сечения балки, необходимо знать ее центроид (или центр масс). Например, если требуется момент инерции секции относительно ее горизонтальной (XX) оси, тогда сначала потребуется вертикальный (y) центроид (пожалуйста, просмотрите наше Учебное пособие о том, как рассчитать центроид секции балки).
Прежде чем мы начнем, если вы искали наш калькулятор свободного момента инерции, щелкните ссылку, чтобы узнать больше. Это вычислит центроид, moi и другие результаты и даже покажет вам пошаговые вычисления! А пока давайте посмотрим на пошаговое руководство и пример того, как рассчитать момент инерции:
Шаг 1. Разделите секцию балки на части
При вычислении момента инерции площади мы должны вычислить момент инерции меньших сегментов.Попробуйте разбить их на простые прямоугольные секции. Например, рассмотрим секцию двутавровой балки ниже, которая также была представлена в нашем руководстве по Centroid. Мы решили разделить эту секцию на 3 прямоугольных сегмента:
Шаг 2: Расчет нейтральной оси (NA)
Нейтральная ось (NA) или горизонтальная ось XX расположена в центре тяжести или центре масс. В нашем руководстве по центроидам центр тяжести этой секции ранее находился на расстоянии 216,29 мм от нижней части секции.
Шаг 3: Расчет момента инерции
Для расчета полного момента инерции секции нам необходимо использовать «Теорему о параллельности оси»:
Поскольку мы разделили его на три прямоугольные части, мы должны вычислить момент инерции каждой из этих частей. Широко известно, что уравнение момента инерции прямоугольника относительно его центральной оси имеет простой вид:
Момент инерции других форм часто указывается на лицевой / оборотной стороне учебников или в этом руководстве по формам момента инерции.Однако прямоугольная форма очень характерна для сечений балок, поэтому, наверное, стоит запомнить.
Теперь у нас есть вся информация, необходимая для использования «Теоремы о параллельной оси» и определения полного момента инерции двутавровой балки. В нашем примере момента инерции:
Итак, у вас есть руководство по расчету площади момента для секций балки. Этот результат имеет решающее значение при проектировании конструкций и является важным фактором отклонения балки.Мы надеемся, что вам понравилось это руководство, и с нетерпением ждем ваших комментариев.
БОНУС: Использование нашего калькулятора момента инерции Учетная запись
SkyCiv показывает полные расчеты момента инерции. Этот интерактивный модуль покажет вам пошаговые расчеты того, как найти момент инерции:
Вы также можете посмотреть результаты нашего калькулятора свободного момента инерции, чтобы проверить свою работу. Это позволит рассчитать все свойства вашего поперечного сечения и является полезным справочным материалом для расчета центроида, площади и момента инерции сечений вашей балки!
Калькулятор свободного момента инерции
Уравнения модуля упругости сечения и калькуляторы Общие формы | Инженеры Edge
Связанные ресурсы: материаловедение
Уравнения и калькуляторы модуля сечения Общие формы
Сопротивление материалов | Прогиб и напряжение балки
Модуль упругости сечения — это геометрическое свойство данного поперечного сечения, используемое при проектировании балок или изгибаемых элементов.Другие геометрические свойства, используемые в конструкции, включают площадь для растяжения, радиус вращения для сжатия и момент инерции для жесткости. Любая связь между этими свойствами сильно зависит от рассматриваемой формы. Уравнения для модулей сечения обычных форм приведены ниже. Есть два типа модулей сечения: модуль упругого сечения (S) и модуль пластического сечения (Z).
Для общего расчета используется модуль упругости сечения, применяемый до предела текучести для большинства металлов и других распространенных материалов.
Модуль упругого сечения определяется как S = I / y, где I — второй момент площади (или момент инерции), а y — расстояние от нейтральной оси до любого данного волокна. Это часто указывается с использованием y = c, где c — расстояние от нейтральной оси до самого крайнего волокна, как показано в таблице ниже. Он также часто используется для определения момента текучести (M y ), такого как M y = S × σ y , где σ y — предел текучести материала.
Расширенный список: Модуль упругости сечения, момент инерции площади, уравнения и калькуляторы
Модуль упругости пластического сечения (PNA)
Модуль упругости пластического сечения используется для материалов, в которых преобладает (необратимая) пластичность. Большинство проектов не сталкиваются с таким поведением намеренно.
Модуль упругости пластического сечения зависит от расположения нейтральной оси пластика (PNA). PNA определяется как ось, которая разделяет поперечное сечение таким образом, что сила сжатия из области сжатия равна силе растяжения из области в области растяжения.Таким образом, для секций с постоянным пределом текучести площадь над и под PNA будет равной, но для составных секций это не обязательно.
Модуль пластического сечения в этом случае представляет собой сумму площадей поперечного сечения на каждой стороне PNA (которые могут быть или не равны), умноженных на расстояние от локальных центроидов двух областей до PNA:
© Copyright 2000-2021, Engineers Edge, LLC www.engineersedge.com
Все права защищены
Отказ от ответственности
| Обратная связь | Реклама
| Контакты
Дата / Время:
Калькулятор свободного момента инерции (второй момент площади)
Как использовать калькулятор свободного сечения
Калькулятор сечения ClearCalcs позволяет пользователю вводить геометрию произвольного поперечного сечения, используя любые простые размеры. формы или полностью настраиваемые определения контуров.Затем он определяет упругие, деформирующие и / или пластические свойства этого сечения, включая площади, координаты центра тяжести, вторые моменты площади / моменты инерции, модули сечения, главные оси, постоянную кручения и многое другое!
Вы можете использовать свойства поперечного сечения из этого инструмента в нашем калькуляторе свободных балок.
Регистрация учетной записи ClearCalcs откроет дополнительные расширенные функции для проектирования и анализа балок и множества других структурных элементов, а также позволит использовать эти пользовательские поперечные сечения в этих проектах.ClearCalcs позволяет проектировать из стали, бетона и дерева в соответствии со стандартами Австралии, США и ЕС.
Лист разделен на два основных раздела:
- «Ключевые свойства», где определяется геометрия поперечного сечения.
- «Сводка», где выбирается тип анализа и отображаются вычисленные свойства.
Раздел «Комментарии» также включен, чтобы пользователь мог оставлять какие-либо конкретные примечания по дизайну. Щелчок по любой из меток ввода / свойства дает описательное справочное объяснение.
1. Свойства входного ключа
Сначала выберите Тип поперечного сечения из раскрывающегося меню чуть ниже диаграммы. Когда вы это сделаете, поля ввода под ним изменится на те, которые требуются для данного типа поперечного сечения.
Например, прямоугольник имеет два измерения, определяющих его: глубина и ширина . Оба размера должны быть больше нуля, но других ограничений нет.
Некоторые другие типы поперечного сечения имеют особые ограничения.Например, двутавровое сечение Глубина должна быть больше, должна быть более чем в два раза больше толщины фланца плюс в два раза больше внутреннего радиуса . Подобные ограничения являются просто логическими ограничениями геометрии; перекрытия или неполные радиусы скругления физически невозможны.
На диаграмме в этом разделе будет показано поперечное сечение в том виде, в каком оно было введено, а также некоторые ключевые свойства этого поперечного сечения, включая центроид, ориентацию главной оси и, если были выполнены соответствующие типы анализа , центр тяжести пластика и центр сдвига.
Выводы сводки вычислений и типы анализа
Доступны четыре различных варианта анализа Тип : «Только эластичность», «Упругость + деформация», «Эластичность + пластик» и «Все». По умолчанию и самый быстрый вариант — «Только эластичность», в то время как другие параметры также добавляют анализ деформации и / или пластичности. Обратите внимание, что эластичный анализ всегда выполняется в каждом варианте. Различные выходные данные, рассчитанные в каждом из этих типов анализа, описаны ниже:
Анализ упругости
- Угол главной главной оси : Большая главная ось (ось «1») может быть наклонена для несимметричных участков или она может быть под углом 90 градусов, если поперечная жесткость сечения больше, чем вертикальная.Это определяет его угол относительно оси X. Обратите внимание, что малая главная ось (ось «2») точно перпендикулярна ей. Ориентация главной оси также указана на диаграмме поперечного сечения.
- Площадь : Площадь поперечного сечения сечения. Это значение обычно используется при определении осевой прочности колонны.
- Первые моменты площади : Первые моменты площади важны для определенных расчетов сдвига, например, сдвигового потока.Обратите внимание, что первые моменты измеряются относительно центроида и геометрических осей.
- Вторые моменты площади / моменты инерции : Вторые моменты площади, также известные в технике как моменты инерции, связаны с силой изгиба и прогибом балки. Обратите внимание, что все значения берутся относительно центра тяжести поперечного сечения, хотя значения доступны как для геометрической, так и для главной осей. Полярный момент инерции идентичен для обоих типов осей, поскольку ось «Z» всегда считается такой же, как ось «3».Момент инерции продукта по определению равен нулю для главных осей.
- Модули упругого сечения : Модули упругого сечения равны вторым моментам площади / моментам инерции, деленным на расстояние до самого дальнего волокна в поперечном сечении, перпендикулярном оси изгиба. Предусмотрены значения как для положительного, так и для отрицательного изгиба, где положительный изгиб определяется как самая верхняя или самая левая часть поперечного сечения, находящаяся в состоянии сжатия. Значения также предоставляются как для геометрической, так и для главной осей и всегда находятся около центра тяжести.N.B. Модуль упругого сечения также известен как модуль статического сечения.
- Расстояние от центра тяжести до крайних волокон : расстояние между центром тяжести поперечного сечения и крайним волокном поперечного сечения, перпендикулярно оси изгиба. Вторые моменты площади / моменты инерции, разделенные на эти расстояния, будут равны модулям упругого сечения.
- Радиусы вращения : Радиусы вращения представляют собой среднеквадратичные расстояния каждого волокна в поперечном сечении относительно данной оси.Значения всегда относятся к центроиду и доступны как по геометрической, так и по главной осям. Полярный радиус вращения идентичен для обоих типов осей, так как ось «Z» всегда считается такой же, как ось «3».
- Центроид : Расположение центроида показано на диаграмме поперечного сечения. Наведите указатель мыши на значок зеленого круга, и всплывающая подсказка отобразит точные координаты центроида. Обратите внимание, что исходная точка (0,0) обозначена синим перекрестием.
Анализ коробления
- Постоянная кручения Сен-Венана : Постоянная кручения связана с тем, насколько хорошо поперечное сечение может противостоять чистым скручивающим силам, и обычно используется в формулах продольного изгиба при поперечном кручении.
- Константа деформации : При приложении силы скручивания или эксцентрика поперечное сечение может не только скручиваться, но и деформироваться. Эта постоянная является мерой того, насколько легко может произойти деформация, и часто используется в формулах продольного изгиба при кручении.
- Зоны сдвига : Только часть поперечного сечения будет эффективно противостоять поперечной силе, приложенной вокруг данной оси (то есть поперечной силе, перпендикулярной данной оси). Показанные значения основаны на интегрировании сдвигового потока и, как таковые, могут не точно соответствовать классическим расчетам, основанным на областях полотна.
- Константы моносимметрии : Константы моносимметрии определяют, насколько близко сечение должно быть симметричным. Константа приближается к нулю, когда поперечное сечение симметрично относительно данной оси.
- Центр сдвига : Расположение центра сдвига показано на диаграмме поперечного сечения. Наведите указатель мыши на значок звездочки, и всплывающая подсказка отобразит точные координаты центра сдвига. Обратите внимание, что исходная точка (0,0) обозначена синим перекрестием.
Анализ пластичности
- Модули пластического сечения : Модули пластического сечения показаны как для геометрической, так и для главной осей. Обратите внимание, что, хотя модуль пластического сечения не зависит от направления изгиба, коэффициент формы, который представляет собой отношение модулей пластического сечения к упругому сечению, зависит от этого.
- Пластиковый центроид : Расположение пластикового центроида показано на диаграмме поперечного сечения. Наведите указатель мыши на оранжевый квадратный значок, и всплывающая подсказка отобразит точные координаты пластикового центроида. Обратите внимание, что исходная точка (0,0) обозначена синим перекрестием.
Момент инерции площади — типичные поперечные сечения I
Момент инерции площади или Момент инерции площади — , также известный как Второй момент площади — I , является свойством формы, которое используется для прогнозирования прогиба, изгиба и напряжения в балках.
Момент инерции площади — Имперские единицы
Момент инерции площади — Метрические единицы
Преобразование между единицами
- 1 см 4 = 10 -8 м 4 = 10 462 4 = 10 мм 4
- 1 дюйм 4 = 4,16×10 5 мм 4 = 41,6 см 4
Пример — Преобразование между площадным моментом единиц инерции 92000 см 66 9 4 можно преобразовать в мм 4 умножением на 10 4
(9240 см 4 ) 10 4 = 9.24 10 7 мм 4
Момент инерции площади (момент инерции площади или второй момент площади)
для изгиба вокруг оси x можно выразить как
I x = ∫ y 2 dA (1)
где
I x = момент инерции площади относительно оси x ( м 4 , мм 4 , дюймы 4 )
y = перпендикулярное расстояние от оси x до элемента dA (м, мм, дюймов )
dA = площадь элемента ( м 2 , мм 2 , дюймов 2 )
Момент инерции изгиба вокруг оси y можно выразить как
90 446 I y = ∫ x 2 dA (2)
где
I y = момент инерции площади относительно оси y ( м 4 , мм 4 , дюймы 4 )
x = перпендикулярное расстояние от оси y до элемента dA (м, мм, дюймов )
Область инерции для типичного поперечного сечения I
Сплошное квадратное поперечное сечение
Момент инерции площади для сплошного квадратного сечения можно рассчитать как
I x = a 4 /12 (2)
где
a = сторона (мм, м, дюйм..)
I y = a 4 /12 (2b)
Сплошное прямоугольное сечение
Момент площади Ineria для прямоугольного сечения можно рассчитать как
I x = bh 3 /12 (3)
где
b = ширина
h = высота
I b 900 3
h / 12 (3b)Сплошное круглое сечение
Момент инерции площади для сплошного цилиндрического сечения можно рассчитать как
I x = π r 4 /4
= π d 4 /64 (4)
где
9 0446 r = радиус
d = диаметр
I y = π r 4 /4
= π d 4 /64 (4b) полый Цилиндрическое поперечное сечение
Момент инерции площади для полого цилиндрического профиля можно рассчитать как
I x = π (d o 4 — d i 4 ) / 64 ( 5)
где
d o = внешний диаметр цилиндра
d i = внутренний диаметр цилиндра
I y = π40 (d 4 — d i 4 ) / 64 (5b)
Квадратное сечение — диагональные моменты
90 002 Моменты инерции диагональной площади для квадратного сечения можно рассчитать как
I x = I y = a 4 /12 (6)
Прямоугольное сечение — Моменты площади на любой линии, проходящей через центр силы тяжести
Прямоугольное сечение и площадь момента на линии, проходящей через центр тяжести, можно рассчитать как
I x = (bh / 12) (h 2 cos 2 a + b 2 sin 2 a) (7)
Симметричная форма
Момент инерции площади для сечения симметричной формы можно рассчитать как
I x = (ah 3 /12) + (b / 12) (H 3 — h 3 ) (8)
I y = (a 3 h / 12) + (b 3 /12) (H — h) ( 8b)
Не симметричная форма
Площадь Момент инерции для несимметричного профиля можно рассчитать как
I x = (1/3) (B y b 3 — B 1 h b 3 + by t 3 — b1 h t 3 ) (9)
Площадь Момент инерции в зависимости отПолярный момент инерции в зависимости от момента инерции
- «Момент инерции площади» — это свойство формы, которое используется для прогнозирования прогиба, изгиба и напряжения в балках
- «Полярный момент инерции» как мера способности балки сопротивление скручиванию — которое требуется для расчета скручивания балки, подверженной крутящему моменту.
- «Момент инерции» — это мера сопротивления объекта изменению направления вращения.
Модуль упругости сечения
- «Модуль упругости сечения» определяется как W = I / y , где I — момент инерции площади, а y — расстояние от нейтральной оси до любого данного волокна
Тройник (T ) свойства раздела | calcresource
Определения
Оглавление
Геометрия
Площадь A и периметр P поперечного сечения тройника можно найти с помощью следующих формул:
\ begin {split} & A & = b t_f + (h-t_f) t_w \\ & P & = 2b + 2h \ end {split}
Расстояние от центра тяжести до верхнего края можно вычислить, если учесть, что первый момент площади (также называемый статическим моментом ) всего Т-образного сечения должно быть равно суммированным статическим моментам стенки и полки:
Ay_c = (t_w h) {h \ over2} + \ Big (\ left (b-t_w \ right) t_f \ Большой) {t_f \ over2} \ Rightarrow
y_c = \ frac {1} {2A} \ left (t_w h ^ 2 + (b-t_w) {t_f} ^ 2 \ right)
У нас есть специальная статья о нахождение центра тяжести составной области.3} {12}
Момент инерции (второй момент или площадь) используется в теории балок для описания жесткости балки при изгибе. Изгибающий момент M, приложенный к поперечному сечению, связан с его моментом инерции следующим уравнением:
M = E \ times I \ times \ kappa
где E — модуль Юнга, свойство материала, и \ kappa, кривизна балки из-за приложенной нагрузки. Следовательно, из предыдущего уравнения видно, что когда к поперечному сечению балки прилагается определенный изгибающий момент M, развиваемая кривизна обратно пропорциональна моменту инерции I.
Полярный момент инерции описывает жесткость поперечного сечения по отношению к крутящему моменту, аналогично описанные выше плоские моменты инерции связаны с изгибом при изгибе. Расчет полярного момента инерции I_z вокруг оси zz (перпендикулярно сечению) можно выполнить с помощью теоремы о перпендикулярных осях:
I_z = I_x + I_y
, где I_x и I_y — моменты инерции вокруг осей. xx и yy, которые взаимно перпендикулярны zz и пересекаются в общей точке начала координат.4.
Модуль упругости
Модуль упругости S_x сечения любого поперечного сечения вокруг оси x-x, которая является центроидальной, описывает реакцию сечения при упругом изгибе при изгибе вокруг той же оси. Он определяется как:
S_x = \ frac {I_x} {Y}
, где I_x — момент инерции секции вокруг оси x, а Y — смещение от центра тяжести секции волокна параллельно оси x-x. Обычно представляет интерес самое удаленное волокно. Для Т-образного сечения модуль упругости S_x сечения вокруг оси x-x не является одинаковым для верхнего и нижнего конца волокна.Поскольку Т-образное сечение не является симметричным относительно оси x, расстояния двух концевых волокон (верхнего и нижнего) от этой оси различаются. Чем больше Y, тем меньше S_x, что обычно предпочтительнее для дизайна секции. Следовательно:
S_ {x, min} = \ frac {I_x} {h-y_c}
, где обозначение «min» основано на предположении, что y_c Для модуля сечения S_y вокруг оси yy, которая для Т-образного сечения оказывается осью симметрии, модуль сечения находится по следующей формуле: S_y = \ frac {I_y} {X} \ Стрелка вправо S_y = \ frac {2 I_y} {b} Если изгибающий момент M_x приложен вокруг оси xx, сечение будет реагировать нормальными напряжениями, линейно изменяющимися с расстоянием от нейтральной оси (которое в упругом режиме совпадает с центроидальная ось xx).3. Модуль упругости пластического сечения аналогичен модулю упругого сечения, но определяется исходя из предположения о полной пластической текучести сечения из-за изгиба при изгибе. В этом случае вся секция делится на две части, одна на растяжение, а другая на сжатие, каждая из которых находится в однородном поле напряжений. Для материалов с равными напряжениями текучести при растяжении и сжатии это приводит к разделению сечения на две равные области, A_t при растяжении и A_c при сжатии, разделенных нейтральной осью.Эта ось называется пластической нейтральной осью , и для несимметричных участков она не совпадает с упругой нейтральной осью (которая также является центроидальной). Модуль упругости пластического сечения определяется по общей формуле: Z = A_c Y_c + A_t Y_t , где Y_c — расстояние от центра тяжести области сжатия A_c от нейтральной оси пластика, а Y_t — соответствующее расстояние от центра тяжести растяжения. площадь А_т. В случае Т-образного сечения при изгибе xx положение пластиковой нейтральной оси может быть определено одним из следующих двух уравнений: \ left \ {\ begin {array} { ll} (h-y_ {pna}) t_w = \ frac {A} {2} & \ text {, if} y_ {pna} \ ge t_f \\ y_ {pna} b = \ frac {A} {2} & \ text {, if} y_ {pna} \ lt t_f \\ \ end {array} \ right. , что становится: y_ {pna} = \ left \ {\ begin {array} {ll} h- \ frac {A} {2t_w} & \ text {, если:} t_f \ le {A \ over2 b } \\ \ frac {A} {2b} & \ text {, если:} t_f \ gt {A \ over2 b} \\ \ end {array} \ right. где y_ \ textit {pna} расстояние пластиковой нейтральной оси от верхнего края фланца. Первое уравнение справедливо, когда пластиковая нейтральная ось проходит через стенку, а второе становится справедливым, когда ось проходит через фланец. Как правило, заранее невозможно узнать, какое уравнение имеет значение.2} {4} \ end {split} Радиус вращения R g поперечного сечения относительно оси определяется по формуле: R_g = \ sqrt {\ frac {I} {A}} , где I момент инерции поперечного сечения относительно той же оси и A его площадь. Модуль упругости
Вокруг оси x
Радиус вращения