Рассчитать площадь: Конвертер единиц площади

Как рассчитать площадь комнаты

Ремонт является хлопотным делом, но одновременно приятным, так как после него, частный дом или квартира становятся уютными, располагающими к отдыху, современными. Как рассчитать площадь комнаты — это, пожалуй, один из главных вопросов, который часто возникает перед началом ремонта.

Можно самостоятельно не заниматься расчетными делами, а доверить это специальной бригаде отделочников, которые будут заниматься самим ремонтом. А что делать, если принято уже решение, что всеми делами будете заниматься самостоятельно? В таком случае, придется заниматься расчетами в особо тщательном режиме, так как отсутствие опыта является результатом переизбытка и нехватки того или иного материала.

Снятие замеров стен

Во всемирной паутине появились не малое количество калькуляторов, которыми можно рассчитать абсолютно все строительные значения, такие как: геометрические объемы, размеры, вес, а также полезную площадь. Не всегда имеется возможность рассчитать квадратный метр с помощью программ. В таких случаях приходится пользоваться обычным способом расчета.

Для расчета обычным способом понадобиться: ручка или карандаш, строительный уровень или длинная рейка, рулетка и соответственно калькулятор.

1. Перед тем как начать мерить, следует освободить как минимум две стены, от загораживающей мебели. Это необходимо, так как при расчете площади комнаты полностью потолка, стен, пола, можно только узнав точные их величины.

2. Для того чтобы рассчитать площадь стен, необходимо взять рулетку и с помощью нее, прикладывая ее к стене по плинтусу измерить величину. Для точности получаемых данных, следует при измерении воспользоваться специальной линией, которую нужно провести ровно, использую при этом уровень (рейку). Полученные результаты сразу нужно записать.

3. Затем, строго вертикально от потолка до пола необходимо провести линию. Для того чтобы удачно ее измерить рулеткой, лучше всего воспользоваться табуреткой, лестницей-стремянкой или столом.

Как правильно рассчитать площадь прямоугольника, понятно, ширина умножается на длину. Если при этом, длина комнаты 5,5 метров, а высота 3 метра, то площадь стены будет равна: 5,5*3=16,5 квадратных метров.

4. Таким же способом необходимо рассчитать и измерить все остальные стены. При имеющихся закруглений или прочих сложных конфигураций, нужно стену поделить на несколько отдельных площадей, и для каждого по отдельности произвести расчеты.

В большинстве случаев, отделка стен в квартирах заключается в покраске или расклейке их обоями. Имеющиеся цифры площадей стен, будут необходимы при подсчете строительных материалов.

Зная площадь стен, как нужно правильно рассчитать обои? Общая сумма площади стен, вполне возможно, что будет иметь отличия от реальной площади, которая подлежит оклейке обоями, так как в комнатах находятся двери, окна. Их необходимо вычесть из общей суммы.

Как узнать общую площадь дверей и окон?

Площадь, которая занята окнами, нужно измерить по его откосам и подоконнику.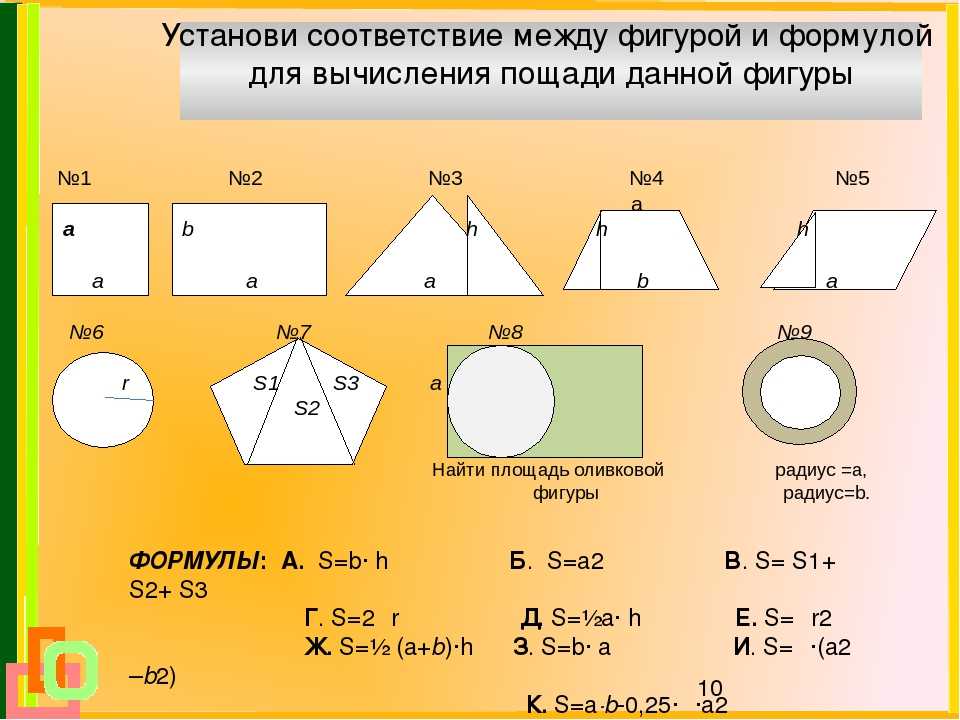 Высота оконного проема определяется по его боковому откосу, а ширина, по его верхнему откосу или же подоконнику.

Например, высота окна 1,65 метров, а ширина 1,55 метров. 1,65*1,55=2,56 квадратных метров.

Если окон два и более, общая их площадь суммируется.

Если окно нестандартной формы, допустим, треугольное, то тут без математических формул не обойтись. Площадь треугольного окна рассчитывается по этой формуле: S=0?5A*h, где A — это нижняя ширина или сторона окна, а h является ее высотой. Если имеется ширина окна, равная 2 метрам, высота 1,5 метра, то общая площадь окна составит: 0,5*1,5*2=1,5 квадратных метров.

Как и площадь прямоугольной стены, площадь дверей измеряется не трудным умножением высоты двери на ее ширину. За основу расчетов необходимо взять снятые уже замеры по коробке, а не по имеющемуся полотну.

Точный расчет обоев на стену

Поклейка обоев, которые не имеют узоров и рисунков, осуществляется без нахлеста по ширине. Учитывая этот момент, покупать можно столько квадратных метров, сколько получится не сложным суммированием площадей абсолютно всех стен за вычетом дверей и окон. Всегда площадь рулона указывается на его упаковке.

Для страхования, при любых покупках обоев, следует приобрести с запасом. Потому как производитель запросто может прекратить выпуск таких обоев, а учитывая возможность мелкого повреждения, например, от детей, появиться желание исправить повреждение.

При учете нахлеста по ширине обоев, на его упаковке должны быть указаны значения полезной площади одного рулона. Опираться стоит из этой цифры.

При выборе обоев с узорами и рисунками, требуется их подгонка. Необходимо учитывать этот момент при расчете, так как будут сдвигаться обои при сопоставлении рисунков или узоров. Приведенными выше примерами было объяснено, как правильно рассчитывать площадь помещения по стенам на их покраску или наклейку обоями.

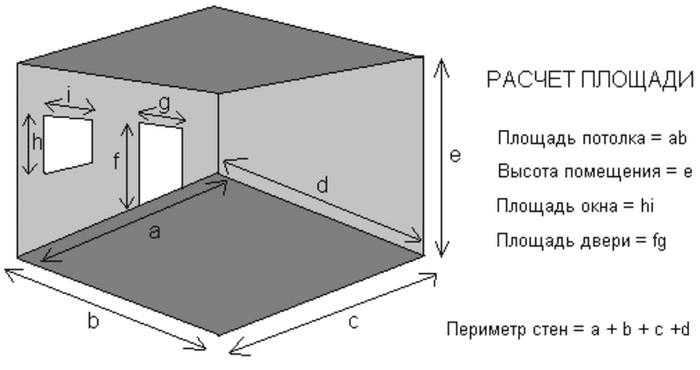
Далее необходимо измерить площадь потолка, пола и в целом, общей площади комнаты или квартиры.

Как рассчитать площадь потолка и пола?

Площадь пола, как известно, равна площади потолка, поэтому можно измерить лишь что-то одно из двух.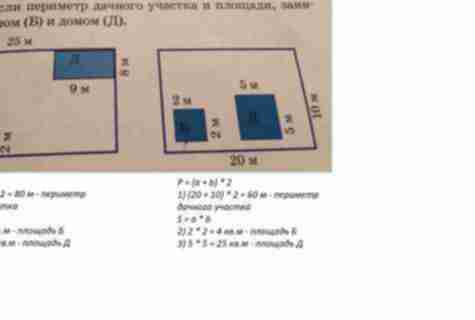

Приведем пример расчета площади комнаты, использую способ определения площади пола. Ширина комнаты 3,5 метра, длина комнаты 5,5 метров. Ширину нужно умножит на длину: 3,5*5,5=19,25 квадратных метров. Итого, площадь пола равна 19,25 квадратных метров.

Площадь потолка будет абсолютно такой же. Шпаклевку, краску на отделку потолка следует рассчитывать исходя из полученных сумм, учитывая при этом запасы, количество слоев, на потолок обои по примеру расчета на стены.

Как определить площадь квартиры или комнаты?

Сумма общей площади помещения, в которой будет проходить ремонт, используют прорабы для того что бы выставить предварительную смету заказчику. Имеются средние цены комплексного ремонта за один квадратный метр, на нее смело можно ориентироваться при подборе подрядчика.

Вести расчеты квадратуры помещения можно использую несколько формул:

1. (А+Б+В+Г)*h=S — это общая площадь, АБВГ — стороны помещения, А, В — 5,55 метров, Б, Г — 3,5 метров.
2. (3,5+5,55+3,5+5,55)*3 = 54,3 квадратных метров.
3. Из общей площади помещения, необходимо вычесть площадь дверей и окон.

Проведение таких подсчетов, во всех помещениях можно узнать, как рассчитать общую площадь жилья.

Вычисление жилой и общей площади квартиры

Для того чтобы выяснить жилую и общую площади квартиры, понадобиться узнать размеры для всех комнат, включая лоджии, встроенные шкафы, кладовки и так далее.

В документациях, получаемые вместе с ключами и ордерами на квартиру, должна отражаться вся необходимая информация о нежилой и жилой площади. На практике, зачастую приходится проводить расчеты повторно.

Для расчета жилой площади квартиры необходимо поэтапно измерить площади всех комнат жилых. Жилым помещением или жилой комнатой называется помещение, пригодное для постоянного в нем проживания, которое отвечает всем санитарно-техническим нормам и правилам. К таким относятся: детская, спальня, гостиная. К нежилым: кладовки, санузлы, кухня и коридор.

Знать площадь и размеры всех нежилых помещений нужно для того, чтобы определить общую площадь квартиры. Так же имеется еще понятие неотапливаемая и отапливаемая площадь квартиры. Оно тесно имеет прямую связь со значением «общая», потому как рассчитывать общую площадь квартиры можно, зная при этом его метраж.

Для включения в общую нежилую площадь веранд, балконов и лоджий, применяются занижающие коэффициенты. Для кладовых и веранд это 1,0; для лоджий это 0,5 и для террас и балконов это 0,3.

Вы спрашивали: как рассчитать площадь звезды

содержание

Как рассчитать звезду?

Как рассчитать звездную величину? Это соотношение может быть выражено математически формулой: m = M + 5 log r(pc) -5, где m и M — видимая и абсолютная величины звезды соответственно, а r(pc) — расстояние до нее от нас в парсеках. .

Как рассчитать радиус звезды?

Как рассчитать радиус звезды? Например: звезда в 4 раза ярче Солнца и в 2 раза горячее, поэтому √4/2 в квадрате. Делая деление, получаем радиус в 0.0113 раза меньше. 0.0113 x 700.000 8000 км ≈ радиус XNUMX км :D.

Как рассчитать площадь пентаграммы?

Если вы знаете его длину, вы можете использовать эту простую формулу.

1. Площадь правильного пятиугольника = pa/2, где a = периметр и a = апофема.
2. Если вы не знаете размер периметра, рассчитайте его по длине стороны (s): p = 5s.

Сколько метров составляет звезда?

Размеры звезд варьируются от массы Юпитера в 70 раз до сверхгигантов, таких как Бетельгейзе в созвездии Ориона, диаметр которой примерно в 650 раз больше диаметра Солнца — около 0,9 миллиарда километров.

Сколько стоит одна звезда?

Сколько стоит каждая звезда на Facebook

За каждую полученную звезду Facebook будет платить вам 0,01 доллара США (долларов США). Когда зрители отправят звезды, вы получите напоминание в чате.

Каков диаметр звезд?

Размер звезд

Однако его диаметр составляет 1 миллиона километров (что эквивалентно примерно 1 миллиону планет Земли).

Что определяет размер звезды?

Его форма обусловлена ​​гравитацией, направленной на ядро ​​звезды. Звезды — это большие сферы плазмы, работающие за счет ядерного синтеза. Звезды — это большие сферы плазмы, удерживаемые вместе собственной гравитацией.

Сколько у тебя звезд?

Наша галактика Млечный Путь насчитывает от 200 до 400 миллиардов звезд. В галактиках в среднем сотни миллиардов звезд. И оценки также указывают на сотни миллиардов галактик во Вселенной. Это привело бы к существованию более 10 секстиллионов звезд.

Чему равна площадь сферы?

Для расчета площади поверхности шара используйте следующую формулу:_SE = 4 . π . г²

Чтобы вычислить значение длины окружности, мы используем формулу C = 2πr, где r — радиус окружности, а π (читай: пи) — константа, представленная этим символом, потому что это повторяющаяся десятичная дробь.

Как вычислить площади фигур?

Как правило, чтобы найти площадь фигуры, просто умножьте основание (b) на высоту (h). Периметр – это сумма отрезков, образующих фигуру, называемых сторонами (l).

Что такое пятиконечная звезда?

Пентаграмма (от древнегреческого πεντάγραμμος, пентаграмма) — звезда, состоящая из пяти прямых линий с пятью точками. Первоначально пятиконечную звезду можно было найти на черепках глиняной посуды, которым более 4 лет.

Как вычислить площадь 5 сторон?

Как вычислить площадь правильного пятиугольника

Другими словами, площадь пятиугольника вычисляется путем умножения периметра многоугольника на его апофему. Стоит отметить, что апофема — это отрезок, идущий от центра правильного многоугольника к центру одной из сторон пятиугольника.

Какова продолжительность жизни звезды?

Время жизни звезды напрямую связано с ее массой.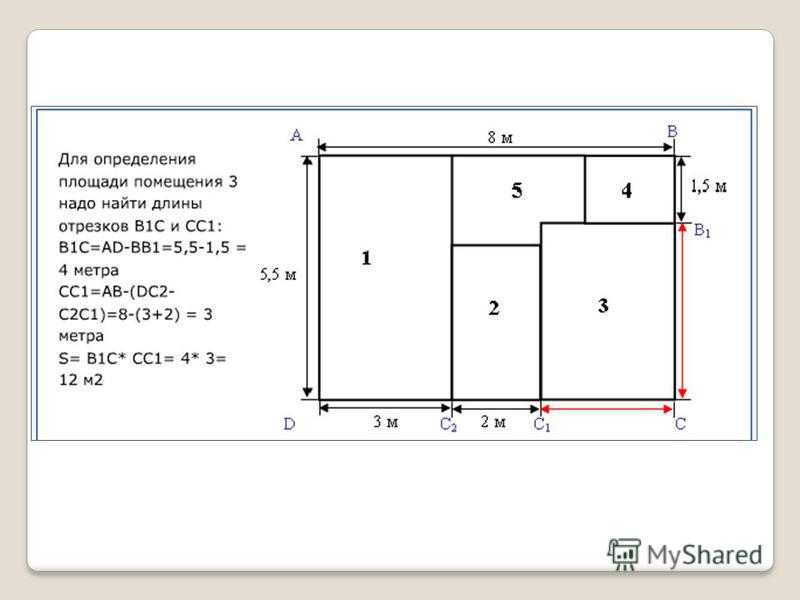 «Те, у которых масса намного больше, чем у Солнца, примерно в десять раз больше, например, просуществуют десятки миллионов лет, в то время как время жизни солнечной звезды составляет 10 миллиардов лет.

Как называется самая большая звезда во Вселенной?

1-й — VY Большого Пса: также известный как VY Cma, этот гипергигант имеет красноватое свечение, его диаметр в 2.100 раз больше, чем у Солнца. Чтобы иметь представление о его величине, внутри него поместилось бы почти три миллиарда планет, равных Земле.

Что внутри звезд?

Звезды состоят в основном из водорода и гелия. Эти элементы остаются объединенными в большую сферу плазмы благодаря сильному гравитационному полю. Превращая водород в гелий, они создают энергию в виде электромагнитных лучей. Поэтому они генерируют свет и тепло.

Как называется самая яркая звезда на небе?

Список самых ярких звезд

	традиционное имя	Величина ап.
0.	Солнце	-26.74
1.	Сириус	-1.46
2.	Canopus	-0.74
3.	Альфа Центавра / Ригель Кент	−0.27 (0.01 + 1.33)

Как называется ближайшая к Земле звезда?

Самая яркая звезда — Альфа Центавра (или Альфа Центавра). Это самая близкая звезда к Земле, за исключением Солнца. В то время как последняя находится примерно в 150 миллионах километров от нашей планеты, Альфа Центавра находится от нас в сорока триллионах километров.

Что больше звезда или Земля?

Так что теоретически звезды больше своих планет, потому что им нужна вся масса, которую они могут захватить, чтобы запустить ядерный синтез.

Как измерить время жизни звезды?

Астрономы рассчитывают возраст звезд по скорости их вращения. Астрономы доказали, что могут точно рассчитать возраст звезды по скорости ее вращения. Мы знаем, что звезды со временем замедляются, но до недавнего времени было слишком мало данных для проведения точных расчетов.

Какова реальная форма звезд?

Звезды — это сферические небесные тела, состоящие из плазмы, состоящей из газов и пыли, в частности гелия и водорода, как мы видели.

Как форма звезды?

Звезды — это сферы, как и планеты. Глядя на звездное небо, мы видим, что звезды мерцают, и это прерывистое свечение создает впечатление маленьких точек вокруг каждой из звезд на небе.

Какая самая маленькая звезда в мире?

Немногим больше Сатурна и в 85 раз массивнее Юпитера небесный объект под названием EBLM J0555-57Ab является самой маленькой звездой, когда-либо идентифицированной и измеренной (Astronomy & Astrophysics, в печати).

Каков вес звезды?

Каков вес звезды? Звезда Солнечной системы имеет приблизительную массу 1,9 нониллиона килограммов — 1,9 и 30 нулей.

Почему Солнце карликовая звезда?

Солнце классифицируется как звезда главной последовательности, то есть оно сплавляет атомы водорода в атомы гелия для производства своей энергии. В рамках этой астрономической классификации Солнце считается желтым карликом.

Сколько звезд видит человеческий глаз?

Ближайшая к Земле звезда – Солнце. У Солнца миллиарды спутников, подавляющее большинство из которых невидимы для наших глаз. При «невооруженном» взгляде человек способен увидеть около 9.000 звезд на ночном небе, и это если считать ночь без облаков и без присутствия Луны.

Как рождаются и умирают звезды?

Сколько проживет звезда, зависит от ее массы. Чем больше масса, тем больше тепла и света она выделит. Его смерть происходит, когда он уже сжег все топливо. Поскольку при этом горении образуются более тяжелые элементы, оно заканчивается только тогда, когда начинается производство железа, а это процесс, требующий потребления энергии.

Чему равно 2 пи в квадрате?

На основе этого открытия длина области, ограниченной окружностью, рассчитывается с использованием математического выражения C = 2 * π * r.

Какова формула шара?

Сфера: Объем = 43πr3. А(всего) = 4πr2.

Что такое формула шара?

Формула объема сферы: V = 4/3 πr³. Посмотрите, как это используется в примере, где у нас есть диаметр сферы.

Каково истинное значение числа Пи?

Поскольку это иррациональное число, оно является неповторяющимся десятичным числом и имеет бесконечные десятичные разряды, поэтому для решения задач обычно используется приближение значения π. Это число является константой, и его значение приблизительно равно 3,141592653…, но наиболее часто используемое приближение для значения π равно 3,14.

Каков объем шара?

Формула объема сферы: V = 4/3 πr³.

Какова площадь треугольника?

Площадь треугольника – это произведение основания и высоты, деленное на 2. Площадь треугольника – это измерение его поверхности, которую можно вычислить, умножив основание на высоту и разделив на два, рассматривая любой треугольник.

Как посчитать площадь по радиусу?

Площадь круга равна числу пи, умноженному на квадрат радиуса (A = π r²).

Что такое диаметр и радиус?

Известные как элементы окружности, мы называем центром или началом точки, которая находится в центре; радиус, отрезок линии, соединяющий центр с окружностью; хорда, любой отрезок, соединяющий два конца окружности; а по диаметру любая хорда, проходящая через центр.

Какая польза от числа пи?

Для чего используется число пи (π)? Число π используется для вычислений с участием круглых тел, таких как площадь круга, длина окружности, объем и площадь цилиндров, конусов, сфер, усеченных конусов и других геометрических тел.

Что такое площадь 5 года?

Площадь равна размеру поверхности, а периметр является результатом суммы ее сторон. В общем, чтобы найти площадь, умножьте основания фигур на высоту (h). По периметру добавляются отрезки прямых, составляющих контур (стороны).

Что такое площадь 4 года?

Площадь – это измерение поверхности.

Поле имеет длину 100 м и ширину 70 м. Чтобы найти площадь, просто перемножьте эти числа.

Что такое плоская местность?

Площадь плоской фигуры – это мера ее поверхности. Для расчета площади плоской фигуры разработаны специальные формулы, зависящие от формы фигуры. Формула площади треугольника. Площадь плоской фигуры – это площадь поверхности фигуры.

Сколько стоит звезда на ничего?

За 54 доллара США (приблизительно 286 реалов) заинтересованные лица могут приобрести то, что компания называет «международным сертификатом» с предполагаемой звездной регистрацией, звездной картой и книгой.

Как мы измеряем звезды во Вселенной?

Поскольку Вселенная такая большая, большинство астрономов не любят измерять расстояния в милях или километрах. Они предпочитают использовать единицу измерения, называемую парсеком. Помните Альфу Центавра, ближайшую к нам звезду? Это 1.347 парсеков или 41.560.000.000.000 41.560 XNUMX XNUMX XNUMX (XNUMX XNUMX триллионов) километров от Земли.

Как рассчитать склонение звезды?

Таким образом, склонение звезды в зависимости от ее положения относительно небесного экватора будет:

1. О северном полюсе: δ = + 90°; Между небесным экватором и северным полюсом: 0º < δ < + 90º;
2. Над небесным экватором: δ = 0°; Между небесным экватором и южным полюсом: 0º > δ > − 90º;
3. О южном полюсе: δ = −90°.

Как измерить время жизни звезды?

Астрономы рассчитывают возраст звезд по скорости их вращения. Астрономы доказали, что могут точно рассчитать возраст звезды по скорости ее вращения. Мы знаем, что звезды со временем замедляются, но до недавнего времени было слишком мало данных для проведения точных расчетов.

Калькулятор площади

| 16 популярных форм!

Создано Hanna Pamuła, PhD

Отзыв от Bogna Szyk и Jack Bowater

Последнее обновление: 02 ноября 2022 г.

Содержание:

• Что такое площадь в математике? Определение площади
• Как рассчитать площадь?
• Формула площади квадрата
• Формула площади прямоугольника
• Формула площади треугольника
• Формула площади круга
• Формула площади сектора
• Формула площади эллипса
• Формула площади трапеции
• Формула площади параллелограмма
• Формула площади ромба
• Формула площади воздушного змея
• Формула площади пятиугольника
• Формула площади шестиугольника
• Формула площади восьмиугольника
• 0 формула
• Площадь четырехугольника формула
• Формула площади правильного многоугольника
• Часто задаваемые вопросы

Если вам интересно, как вычислить площадь любой базовой фигуры, вы находитесь в правильном месте — этот калькулятор площади ответит на все ваши вопросы. Используйте наш интуитивно понятный инструмент, чтобы выбрать одну из шестнадцати различных фигур и вычислить их площадь в мгновение ока. Ищете ли вы определение площади или, например, площадь формулы ромба, мы обеспечим вас. Продолжайте прокручивать, чтобы узнать больше, или просто поиграйте с нашим инструментом — вы не будете разочарованы!

Что такое площадь в математике? Определение площади

Проще говоря, площадь — это размер поверхности . Другими словами, его можно определить как пространство, занимаемое плоской формой. Чтобы понять концепцию, обычно полезно представить площадь как количество краски, необходимое для покрытия поверхности . Посмотрите на рисунок ниже – все фигуры имеют одинаковую площадь, 12 квадратных единиц:

Существует множество полезных формул для вычисления площади простых фигур. В разделах ниже вы найдете не только известные формулы для треугольников, прямоугольников и окружностей, но и другие формы, такие как параллелограммы, воздушные змеи или кольца.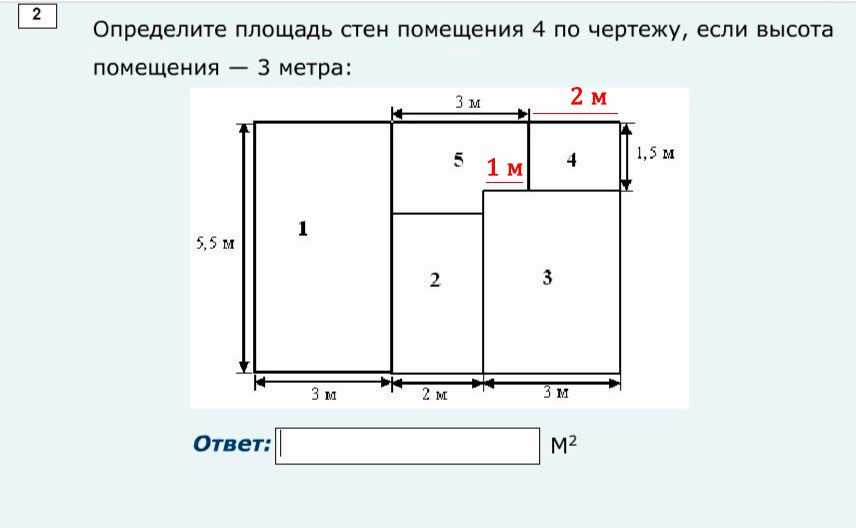

Мы надеемся, что после этого объяснения у вас не возникнет проблем с определением области математики!

Как рассчитать площадь?

Ну конечно, это зависит от формы ! Ниже вы найдете формулы для всех шестнадцати фигур, представленных в нашем калькуляторе площади. Для ясности мы перечислим только уравнения — их изображения, пояснения и выводы можно найти в отдельных абзацах ниже (а также в инструментах, посвященных каждой конкретной фигуре).

Вы готовы? Вот самые важные и полезные формулы площади для шестнадцати геометрических фигур:

• Квадрат формула площади: A = a²
• Прямоугольник Формула площади: A = a × b
• Формулы площади треугольника :
  • А = b × h / 2 или
  • A = 0,5 × a × b × sin(γ) или
  • A = 0,25 × √( (a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c)) или
  • A = a² × sin(β) × sin(γ) / (2 × sin(β + γ))
• Круг формула площади: A = πr²
• Сектор круга Формула площади: A = r² × угол / 2
• Эллипс формула площади: A = a × b × π
• Трапеция Формула площади: A = (a + b) × h / 2
• Формулы площади параллелограмма :
  • А = а × ч или
  • A = a × b × sin(угол) или
  • A = e × f × sin(угол)
• Ромб Формулы площади:
  • А = а × ч или
  • А = (е × f) / 2 или
  • A = s² × sin(угол)
• Кайт формулы площади:
  • А = (е × f) / 2 или
  • А = а × b × sin(γ)
• Формула площади Пентагона : A = a² × √(25 + 10√5) / 4
• Шестиугольник Формула площади: A = 3/2 × √3 × a²
• Октагон формула площади: A = 2 × (1 + √2) × a²
• Формула площади кольца : A = π(R² - r²)
• Четырехугольник формула площади: A = e × f × sin(угол)
• Правильный многоугольник Формула площади: A = n × a² × cot(π/n) / 4

Хотите изменить единицу площади? Просто нажмите на название устройства, и появится раскрывающийся список.

Формула площади квадрата

Вы забыли, что такое формула площади квадрата? Тогда вы находитесь в правильном месте. Площадь квадрата равна произведению длины его сторон:

• Площадь квадрата = a × a = a² , где a — сторона квадрата

Это самая основная и наиболее часто используемая формула, хотя существуют и другие. Например, есть формулы площади квадрата, в которых используются диагональ, периметр, радиус описанной окружности или внутренний радиус.

Формула площади прямоугольника

Формула площади прямоугольника тоже несложна — это просто произведение сторон прямоугольника:

• Площадь прямоугольника = a × b

Расчет площади прямоугольника чрезвычайно полезен в повседневных ситуациях: от строительства здания (оценка необходимой плитки, настила, сайдинга или определения площади крыши) до отделки вашей квартиры (сколько мне нужно краски или обоев?) до расчета, сколько люди, которых ваш торт может накормить.

Формула площади треугольника

Существует много различных формул для площади треугольника, в зависимости от того, что дано и какие законы или теоремы используются. В этом калькуляторе площади мы реализовали четыре из них:

1. Даны основание и высота

• Площадь треугольника = b × h / 2

2. Даны две стороны и угол между ними (SAS)

• Площадь треугольника = 0,5 × a × b × sin(γ)

3. Даны три стороны (SSS) (Эта формула площади треугольника называется Формула Герона )

• Площадь треугольника = 0,25 × √( (a + b + c) × (-a + b + в) × (а - б + в) × (а + б - в))

Вы можете узнать больше в калькуляторе формул Герона.

4. Даны два угла и сторона между ними (ASA)

• Площадь треугольника = a² × sin(β) × sin(γ) / (2 × sin(β + γ))

Существует особый тип треугольника, прямоугольный треугольник. В этом случае основание и высота — это две стороны, образующие прямой угол. Тогда площадь прямоугольного треугольника может быть выражена как:

Площадь прямоугольного треугольника = a × b / 2

Формула площади круга

Формула площади круга является одной из самых известных формул:

• Площадь круга = πr² , где r — радиус круга

В этом калькуляторе мы реализовали только это уравнение, но в нашем калькуляторе круга вы можете рассчитать площадь по двум разным формулам:

1. Диаметр

• Площадь круга = πr² = π × (d / 2)²

2. Окружность

• Площадь круга = c² / 4π

Кроме того, формула площади круга удобна в повседневной жизни – например, при решении серьезной дилеммы, какой размер пиццы выбрать.

Формула площади сектора

Формулу площади сектора можно найти, взяв пропорцию окружности. Площадь сектора пропорциональна его углу, поэтому, зная формулу площади круга, мы можем написать, что:

α / 360° = площадь сектора / площадь круга

Преобразование угла говорит нам, что 360° = 2π

α / 2π = Площадь сектора / πr²

Итак:

• Площадь сектора = r² × α / 2

Формула площади эллипса

Чтобы найти формулу площади эллипса, сначала вспомните формулу площади круга: πr² . Для эллипса у вас есть не одно значение радиуса, а два разных значения: a и b . Единственная разница между формулами площади круга и эллипса заключается в замене r² произведением большой и малой полуосей, a × b :

• Площадь эллипса = π × a × b

Формула площади трапеции

Площадь трапеции можно найти по следующей формуле:

• Площадь трапеции = (a + b) × h / 2 , где a и
  74 длины параллельных сторон и высота

  Кроме того, формула площади трапеции может быть выражена как:

  Площадь трапеции = m × h , где м — среднее арифметическое длин двух параллельных сторон

  Площадь параллелограмма формула

  Хотите ли вы вычислить площадь, зная основание и высоту, стороны и угол, или диагонали параллелограмма и угол между ними, вы находитесь в правильном месте. В нашем инструменте вы найдете три формулы площади параллелограмма:

  1. Основание и высота

  • Площадь параллелограмма = a × h

  2. Стороны и угол между ними

  • Площадь параллелограмма = a × b × sin(α)

  3. Диагонали и угол между ними

  • Площадь параллелограмма = e × f × sin(θ)

  Формула площади ромба

  Мы реализовали три полезные формулы для вычисления площади ромба. Вы можете найти площадь, если знаете:

  1. Сторона и высота

  • Площадь ромба = a × h

  2. Диагонали

  • Площадь ромба = (e × f) / 2

  3. Сторона и любой угол, например, α

  • Площадь ромба = a² × sin(α)

  Площадь воздушного змея по формуле

  Для расчета площади воздушного змея можно использовать два уравнения, в зависимости от того, что известно:

  1. Площадь воздушного змея по формуле с учетом диагоналей воздушного змея

  • Площадь воздушного змея = (e × f) / 2

  2. Площадь воздушного змея по формуле с двумя неконгруэнтными сторонами и углом между этими двумя сторонами

  • Площадь воздушного змея = a × b × sin(α)

  Формула площади пятиугольника

  Площадь пятиугольника можно рассчитать по формуле:

  • Площадь пятиугольника = a² × √(25 + 10√5) / 4 , где - сторона 9007 правильный пятиугольник

  Воспользуйтесь нашим специальным калькулятором пятиугольника, где представлены другие основные свойства правильного пятиугольника: сторона, диагональ, высота и периметр, а также радиус описанной и вписанной окружности.

  Формула площади шестиугольника

  Основная формула площади шестиугольника:

  • Площадь шестиугольника = 3/2 × √3 × a² , где a — сторона правильного шестиугольника

  Итак, откуда берется формула? Вы можете думать о правильном шестиугольнике как о наборе шести конгруэнтных равносторонних треугольников. Чтобы найти площадь шестиугольника, нам нужно найти площадь одного треугольника и умножить ее на шесть. Формула площади правильного треугольника равна квадрату стороны, умноженному на квадратный корень из 3, деленному на 4:

  Площадь равностороннего треугольника = (a² × √3) / 4

  Площадь шестиугольника = 6 × Площадь равностороннего треугольника = 6 × (a² × √3) / 4 = 3/2 × √3 × a²

  Формула площади восьмиугольника

  Чтобы найти площадь восьмиугольника, все, что вам нужно сделать, это знать длину стороны и следующую формулу:

  • Площадь восьмиугольника = 2 × (1 + √2) * a²

  Площадь восьмиугольника также может быть рассчитана по формуле:

  Площадь восьмиугольника = периметр × апофема / 2

  Периметр в восьмиугольном случае — это просто 8 × a . А что такое апофема? Апофема — это расстояние от центра многоугольника до середины стороны.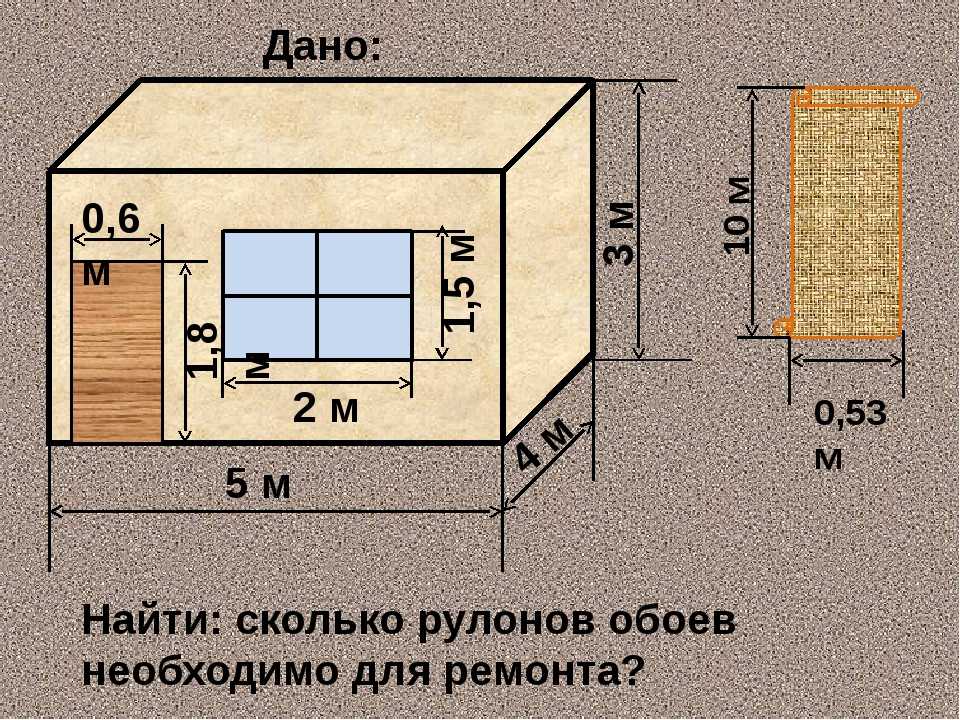 В то же время это высота треугольника, полученного путем проведения линии из вершин восьмиугольника в его центр. Этот треугольник — один из восьми конгруэнтных — является равнобедренным, поэтому его высота может быть рассчитана, например, с помощью теоремы Пифагора по формуле:

  h = (1 + √2) × a / 4

  Итак, наконец, мы получаем первое уравнение:

  Площадь восьмиугольника = периметр * апофема / 2 = (8 × a × (1 + √2) × a / 4) / 2 = 2 × (1 + √2 ) × a²

  Площадь кольца формула

  Кольцо представляет собой кольцеобразный объект – область, ограниченную двумя концентрическими окружностями разного радиуса. Найти площадь по формуле кольца несложно, если вы помните формулу площади круга. Только взгляните: площадь кольца — это разность площадей большего круга радиуса R и меньшего круга радиуса r:

  • Площадь кольца = πR² - πr² = π(R² - r²)

  Формула площади четырехугольника

  Формула четырехугольника, которую реализует этот калькулятор площади, использует две заданные диагонали и угол между ними.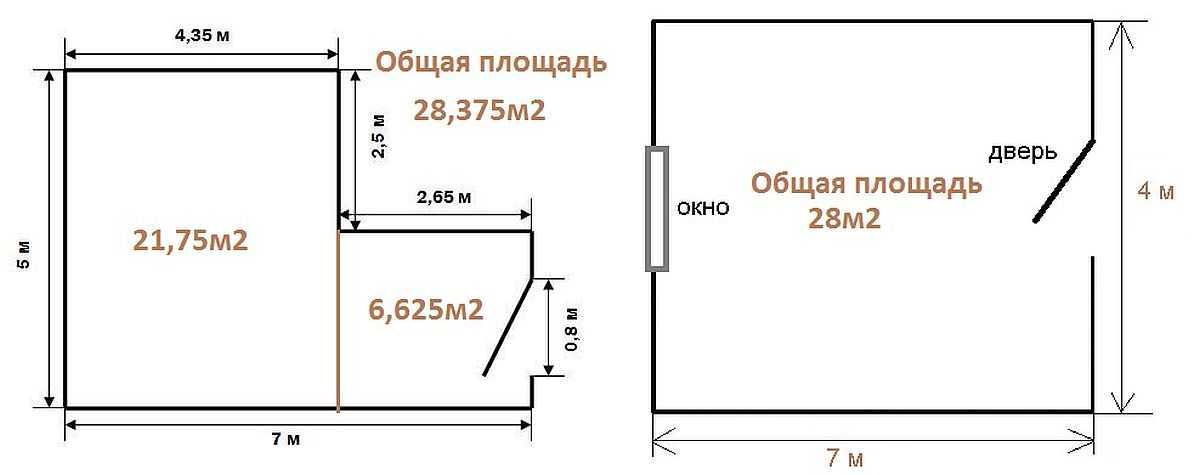

  • Площадь четырехугольника = e × f × sin(α) , где e и f — диагонали.

  Мы можем использовать любой из двух углов при вычислении их синуса. Зная, что два смежных угла дополнительные, можно утверждать, что sin(угол) = sin(180° - угол) .

  Если вы ищете другие формулы площади четырехугольника, воспользуйтесь нашим специальным калькулятором четырехугольника, где вы найдете формулу Бретшнайдера (для четырех сторон и двух противоположных углов) и формулу, в которой используются бимедианы и угол между ними. их.

  Формула площади правильного многоугольника

  Формула площади правильного многоугольника выглядит следующим образом:

  • Площадь правильного многоугольника = n × a² × cot(π/n) / 4

  , где n — количество сторон, а — длина стороны.

  Существуют и другие уравнения, в которых используются, например, такие параметры, как радиус описанной окружности или периметр.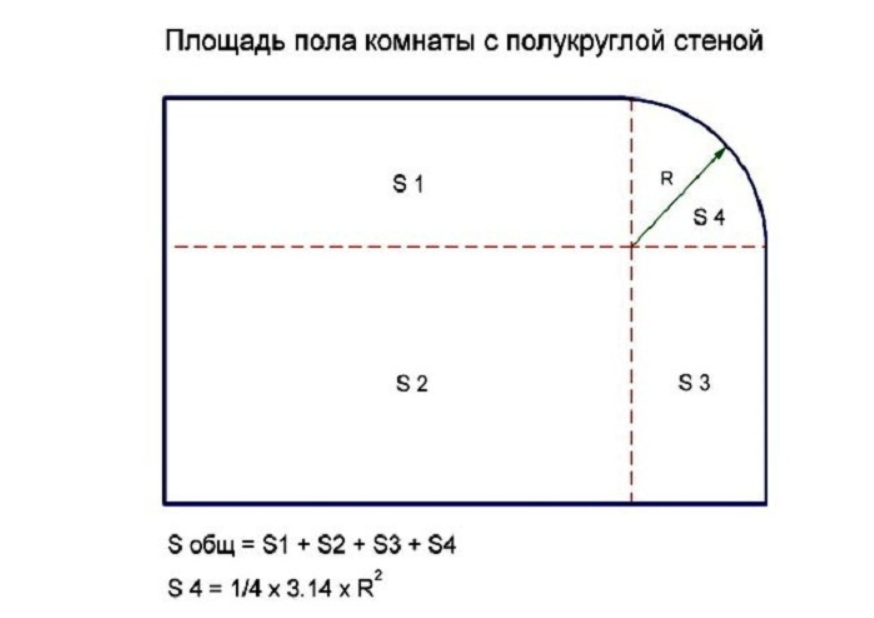 Вы можете найти эти формулы в специальном параграфе нашего калькулятора площади многоугольника.

  Если вы имеете дело с неправильным многоугольником, помните, что вы всегда можете разделить фигуру на более простые фигуры, например, на треугольники. Просто посчитайте площадь каждого из них и, в конце, просуммируйте их. Разложение многоугольника на множество треугольников называется триангуляцией многоугольника.

  Часто задаваемые вопросы

  Какой четырехугольник имеет наибольшую площадь?

  Для заданного периметра четырехугольник с максимальной площадью всегда будет квадратом .

  Какая фигура имеет наибольшую площадь при заданном периметре?

  Для заданного периметра замкнутая фигура максимальной площади представляет собой круг .

  Как рассчитать площадь неправильной формы?

  Чтобы вычислить площадь неправильной формы:

  1. Разделите фигуру на несколько частей, для которых можно легко вычислить площадь, например треугольники, прямоугольники, трапеции, (полу)круги и т. д.
  2. Вычислите площадь каждой из этих подформ.
  3. Суммируйте площади подформ, чтобы получить окончательный результат.

  Как рассчитать площадь под кривой?

  Чтобы найти площадь под кривой на интервале, необходимо вычислить определенный интеграл функции, описывающей эту кривую, между двумя точками, соответствующими концам рассматриваемого интервала.

  Ханна Памула, PhD

  Площадь круга

  Посмотрите 23 похожих калькулятора 2D-геометрии 📏

  Площадь прямоугольникаПлощадь полумесяцаЦентр масс… Еще 20

  Калькулятор площади 📐 - Рассчитайте площадь квадрата, прямоугольника, треугольника, круга, параллелограмма, трапеции...

      Быстрая навигация:

  1. вычислить площадь любой фигуры?
  2. Площадь квадрата
  3. Площадь прямоугольника
  4. Площадь треугольника
  5. Площадь круга
  6. Площадь параллелограмма
  7. Площадь трапеции
  8. Площадь эллипса (овала)
  9. Площадь сектора
  10. Площадь восьмиугольника
  11. Где использовать калькулятор площади?
      Как вычислить площадь любой фигуры?

  Каждая геометрическая фигура имеет свою формулу для вычисления площади и разные требуемые размеры, которые необходимо знать. См. ниже подробную информацию о каждом отдельном калькуляторе площади, который поддерживает этот калькулятор площади, включая используемую формулу. При выполнении измерений или чтении планов убедитесь, что все измерения указаны в одних и тех же единицах измерения, или преобразуйте их в одни и те же единицы, чтобы получить достоверный результат. Результатом всегда является единица измерения в квадрате, например. квадратные сантиметры, квадратные километры, квадратные дюймы, квадратные футы, квадратные мили...

  Расчет площади применяется в строительстве и отделке помещений (например, требуется покраска), в управлении земельными ресурсами, сельском хозяйстве, биологии, экологии и многих других дисциплинах.

      Площадь квадрата

  Формула площади квадрата: сторона ² , как показано на рисунке ниже:

  единичное измерение. Однако, поскольку в большинстве практических ситуаций вам нужно измерить обе стороны, прежде чем вы узнаете, что это квадрат, разница может быть невелика, но, по крайней мере, ее легче вычислить.

  
  
      Площадь прямоугольника

  Формула площади прямоугольника: ширина x высота , как показано на рисунке ниже:

  и просто умножить их вместе. Это одна из самых простых фигур для вычисления площади. Неправильные формы часто разбивают на ряд прямоугольников, чтобы можно было приблизительно рассчитать их площадь.

      Площадь треугольника

  Формула площади треугольника: высота x π x (радиус / 2) ² , где (радиус / 2) - радиус основания (d = 2 x r), так что другой способ записи это высота x π x радиус ² . Визуально на рисунке ниже:

  Несмотря на простоту приведенного выше уравнения, в определенных ситуациях вы можете не знать эти два точных измерения. Существует несколько правил вычисления площади треугольника: SSS (сторона-сторона-сторона), SAS (две стороны и прилежащий угол), SSA (две стороны и не заключенный между ними угол), ASA (два угла и прилежащая сторона).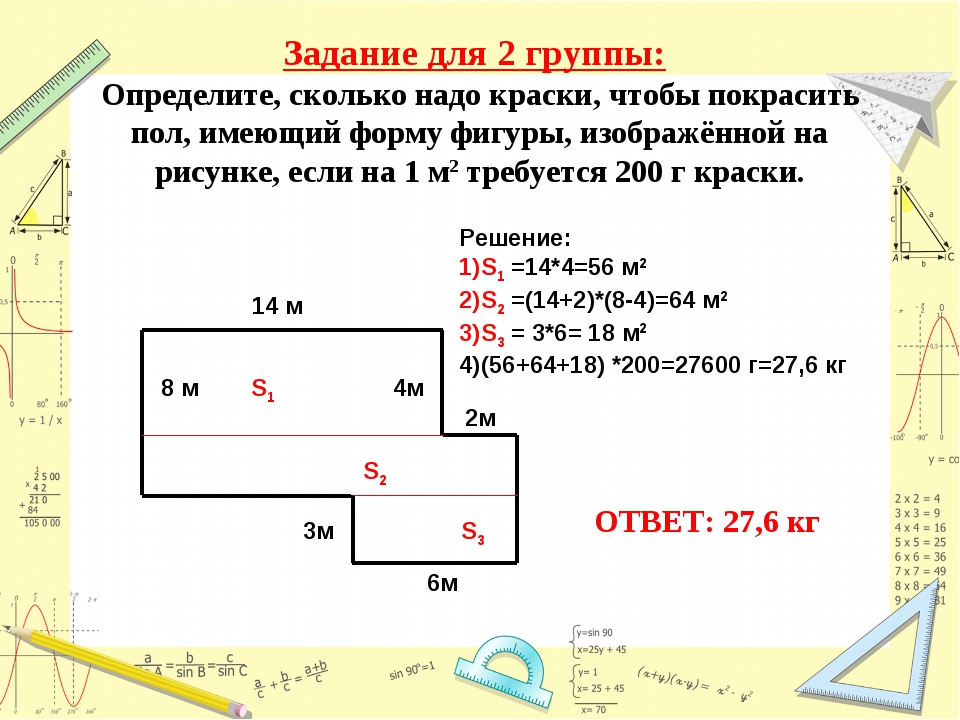 . Для прямоугольных треугольников вы можете вычислить площадь, зная гипотенузу и высоту к ней. Все они поддерживаются этим онлайн-калькулятором площади.

  
  
      Площадь круга

  Формула площади круга: π x радиус ² , но диаметр круга равен d = 2 x r, поэтому его можно записать по-другому: π х (диаметр / 2) ² . Визуально на рисунке ниже:

  Для площади круга вам нужен только его радиус. В большинстве практических ситуаций было бы проще рассчитать диаметр, поэтому наш калькулятор использует диаметр в качестве входных данных.

      Площадь параллелограмма

  Формула площади параллелограмма равна ширина x высота , как показано на рисунке ниже: к прямоугольнику для вычисления площади, таким образом, формула в основном такая же, но мы используем высоту параллелограмма вместо его стороны.

  
  
      Площадь трапеции

  Формула площади трапеции: (основание 1 + основание 2) / 2 x высота , как показано на рисунке ниже:

  особенно с помощью калькулятора площади. Трапецию можно преобразовать в прямоугольник, зная длину каждого основания и его высоту, так что это минимальные необходимые измерения.

      Площадь эллипса (овала)

  Формула площади эллипса: π x большой радиус x малый радиус , как показано на рисунке ниже:

  Площадь овала аналогична площади круга, но поскольку у него два радиуса, немного отличается. Здесь вы можете измерить два диаметра и разделить на два, чтобы получить два радиуса.

  
  
      Площадь сектора

  Формула площади сектора: (угол / 360) x π x радиус , но диаметр круга равен d = 2 x r, так что другой способ записи (угол / 360) 2 x π x (диаметр / 2) . Визуально на рисунке ниже:

  Поскольку сектор — это просто срез круга, формула очень похожа на формулу для площади круга, с той разницей, которая необходима для расчета того, какую часть круга покрывает сектор. В то время как радиус легко измерить, угол — нет, если только у вас нет под рукой надлежащего инструмента, который может быть необходимым условием для использования нашего калькулятора площади.

  Рассчитать площадь: Конвертер единиц площади