Как самому посчитать количество ламината
Как рассчитать площадь помещения и понять — сколько нужно упаковок ламината
Самый простой способ расчета количества ламината, которым пользуются тысячи людей во всем мире.
Метод этот настолько прост, что многие даже не думают о нем, но поверьте это самый эффективный приём, который исключит возможные ошибки. Для расчета вам понадобятся следующие исходные данные: площадь помещения, где будет лежать ламинат — умножьте длину помещения на ширину помещения и запишите получившуюся цифру с двумя знаками после запятой. Следующее, что вам нужно будет сделать — определиться, какой именно ламинат вы хотели бы постелить — торговая марка, коллекция.
Когда у вас на руках есть площадь вашего помещения и примерное представление — какой ламинат вы планируете постелить в помещении, возьмите ваш телефон и ПОЗВОНИТЕ В ЛЮБОЙ МАГАЗИН с ламинатом в вашем городе. И вам все посчитают без ошибок )))
А если этот вариант вам не подходит, то ниже изложен другой, более сложный способ.
Пошаговая инструкция по расчету количества ламината для тех, кто стесняется позвонить по телефону
Запланировали купить ламинат, но есть трудности с расчетом количества материала? Тогда читайте эту статью и у вас больше не возникнет никаких сложностей.
Вычисление требуемого количества пачек ламината для вашей площади происходит в несколько этапов:
- Точный расчет площади помещения
- Выбор ламината
- Определение квадратуры пачки выбранного ламината
- Окончательный расчет количества пачек
Измерение площади пола
Если ваше помещение имеет необычную форму, то условно разбивайте его на несколько простых фигур, чтобы легче было рассчитать вашу площадь.
Для правильного расчета количества ламината требуется знать точную квадратуру площади, где будет стелиться напольное покрытие. Рулеткой измеряем длину и ширину комнаты и получившиеся указатели умножаем друг на друга.
Запишите получившуюся цифру.
Для помещения разных форм способы расчета площади отличаются.
Расчет простой площади
Если у вас стандартное помещение прямоугольной формы, то высчитать площадь очень просто
Расчет площади изогнутого помещения
Если у вас нестандартное помещение изогнутой формы, то смотрите на схему ниже.
Расчет площади сложного помещения
Если у вас нестандартное помещение, в котором имеются стены, расположенные не параллельно друг другу, то смотрите схему для расчета подобных площадей.
Выбор ламината
Для расчета вам нужно знать — сколько квадратных метров ламината в одной упаковке.
Если вы еще не купили ламинат, но где-то видели то, что вам понравится — поинтересуйтесь, что это за коллекция и какая это торговая марка. Имея эти данные, вы легко можете узнать — сколько точно квадратных метров ламината в одной упаковке. Обычно такая информация указана на ценниках в магазине, либо в интернете.
Если вам в магазине дали каталог с интересующей вас коллекцией, то подобную информацию ищите на последних страницах каталога.
Точный расчет количества упаковок ламината
Используйте формулу:
(Площадь помещения + X % на подрезки) / м2 в упаковке
Итак, все что нужно для окончательных расчетов у вас имеется.
Формула расчета выглядит следующим образом:
(S1+x%)/S2 = N
S1 — это чистая общая площадь помещения в квадратных метрах.
S2 — количество квадратных метров ламината в одной упаковке
x% — это процент подрезки (расход ламината, который необходимо учесть при будущей укладке). Если вы планируете стандартную укладку ламината вдоль помещения (или поперек, главное что продольные швы будут тянуться параллельно стенам) то в среднем закладывают 5% на подрезку. Если направление укладки предполагается по диагонали, тогда стоит прибавить уже 10-12%.
В итоге вы получите число N с несколькими знаками после запятой. Это число стоит округлить в большую сторону. Получившееся целое число и есть требуемое количество пачек конкретного ламината для вашего помещения.
Пример расчета количества ламината My Floor
Дано:
- Комната размером 3,2 метра на 4,8 метров.
- Выбран ламинат My Floor коллекция Cottage дизайн Дуб бежевый атласный
- Укладка прямая
1. Рассчитываем чистую площадь помещения
Берем имеющиеся размеры помещения. 3,2 метра умножаем на 4,8 метров, получаем 15,36 квадратных метров.
2. Прибавляем процент подрезки
Поскольку предполагается прямая укладка, то к получившемуся числу 15,36 надо прибавить 5% на подрезку. Получаем 16,128
3. Смотрим квадратуру пачки выбранного ламината
Ламинат My Floor коллекция Cottage дизайн Дуб бежевый атласный (можно посмотреть на соответствующей странице сайта) имеет квадратуру пачки 2,1316 квадратных метров.
4. Делим площадь помещения на площадь одной упаковки ламината
Число, которое мы получили в пункте 2 мы должны поделить на количество квадратных метров у одной упаковке. Берем 16,128 и делим на 2,1316. Получаем 7,566
5. Округляем
Получившееся число 7,566 надо округлить в большую сторону. Получаем 8.
Итог — для помещения размером 3,2 на 4,8 метров, ламината My Floor Cottage Дуб бежевый атласный нам понадобится 8 упаковок.
Остались вопросы? Хотите уточнить какие-нибудь моменты?
Обращайтесь к специалистам Ламинат Плюс.
+7(983) 615 00 80
Как посчитать площадь комнаты стен потолка пола и высчитать квадратуру квартиры в квадратных метрах
Читай, смотри и всë получится!
Здравствуйте, дорогие читатели! Уделяем немного времени для решения такого вопроса как подсчет площадей: стен, пола, потолка и высчитываем квадратуру комнаты и всей квартиры.
Ведь для расчета стройматериалов необходимы правильные расчеты. Начнём по порядку!
Подсчет общей площади комнаты ведется в квадратных метрах, для этого нужно длину комнаты умножить на ширину. Рулеткой замеряем от стены до стены длину комнаты, а потом ширину.
Например, длина комнаты 4 метра, а ширина 3 метра. Умножаем длину на ширину 4х3 и получаем 12 квадратных метров или 12 метров в квадрате – (одно и то же).
Квадратная площадь нашей комнаты ровна 12 метрам.
Посчитать площадь стен
Для подсчета площади всех стен необходимо высчитать площадь каждой стены по отдельности.
Подсчитываем площадь каждой стены.
Рулеткой замеряем высоту стены от пола до потолка, получилось, например, 2 метра 80 сантиметров. Теперь замеряем длину стены от угла до угла, получилось, например, 4 метра 50 сантиметров. Умножаем высоту стены на длину стены 2,8 м умножить на 4,5 м, и получаем общую площадь стены 12 метров 60 сантиметров, т.е. 12,6 квадратных метров.
Со второй стеной проделываем тоже самое: высоту стены умножаем на длину стены и получаем площадь второй стены, например, 12,6 метров в квадрате.
Далее по очереди вычисляем и складываем площади всех стен и получаем общую площадь стен в квадратных метрах.
Будьте внимательны для закупки смесей, грунтовок, красок или стройматериалов необходимо отнять окна и дверные проёмы от общей площади стен.
Посчитать площадь потолка
При подсчете площади потолка необходимо рулеткой померить его длину и ширину, после чего умножить получившиеся размеры.
Например, ширина 3,5 метра, а длина 4,40 м.
Нужно 3,5 умножить на 4,40 получится 15,4 квадратных метров – это общая площадь нашего потолка в комнате.
Посчитать площадь пола
Обычно площадь пола равна площади потолка и если на полу много материала и нет возможности сделать правильные замеры пола, можно ориентироваться на потолок. При этом учитывайте ровность стен.
Но если все-таки необходимо сделать точные замеры, то нужно померить ширину и длину пола. После чего умножить эти величины. Например, ширина пола 3 метра, а его длинна 4 метра, т.е. умножаем 3 на 4 и получаем площадь пола равную 12-ти квадратным метрам.
Квадратура комнаты
Если комната прямоугольной или квадратной формы, то квадратурой будет являться её длина, умноженная на ширину. Например, длинна 5 метров, ширина 4 метра, квадратура комнаты равна 20 кв.
м.
Если комната имеет разные фигуры, например треугольник, полукруг (эркер), то для подсчета квадратуры комнаты нужно визуально разбить все получившиеся площади на отдельные фигуры и сложить их вместе:
- треугольник в комнате 3 кв. м.;
- эркер 5 кв. м.;
- прямоугольник 12 кв. м.
Далее складываем все фигуры 3+5+12=20 кв. м. это вся квадратура комнаты.
Квадратура квартиры
Чтобы посчитать квадратуру квартиры, с начало нужно высчитать квадратуру каждой комнаты по отдельности, а потом сложить получившиеся площади вместе.
При расчетах для закупки смесей и материалов учитывайте (вычитайте) дверные и оконные проёмы.
Рекомендую закупать на 5-7 % больше материалов: ламината, плитки, плинтуса и т.п. на непредвиденные расходы по подрезанию, подгонке по форме и рисунку.
Важное в ремонте это решение, а здесь их много – сохраняйте в закладках сайт по ремонту квартиры от Виктора и делайте всё своими руками!
Автор статьи: Рябенко Виктор Николаевич
Ремонт квартиры своими силами
Читай, смотри и всë получится!
k d\mu(\xi), &k > p \конец{случаи}, $$ таким образом, $m_k$ должен быть полностью монотонным.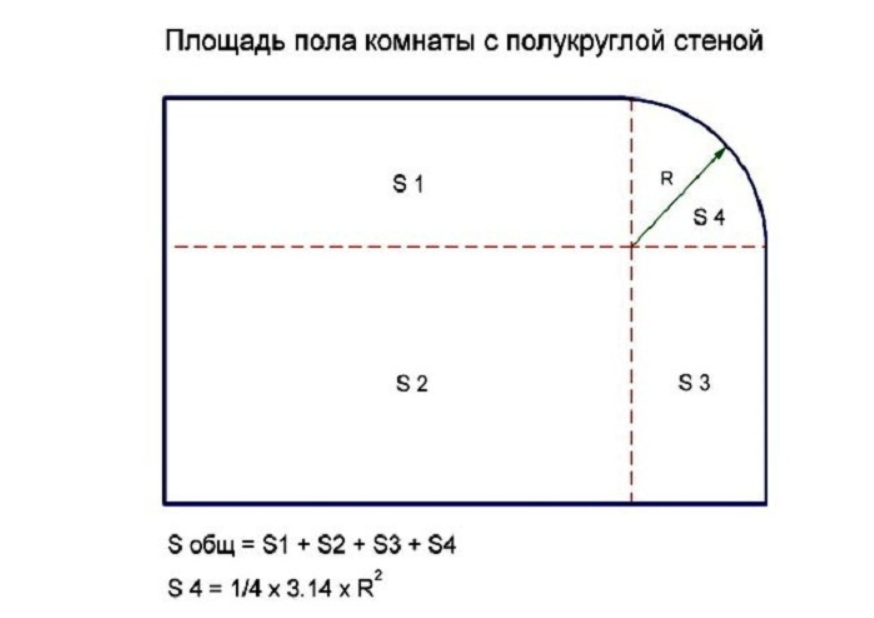
n |w_i|\\
\operatorname*{при условии} &&&0 \leq \xi_1\\
&&&\xi_1 \leq \xi_2\\
&&&\xi_2 \leq \xi_3\\
&&&\vdots\\
&&&\xi_{n-1} \leq \xi_n\\
&&&\xi_n \leq 1\\
&&&\delta_{k} = 0, \quad k = 0, 1, \dots, p
\end{выровнено}
$$С помощью GAMS/BARON я нашел несколько таких квадратур (вы также можете использовать сервер NEOS для решения моделей GAMS)
Для $p = 4$
Задача кажется неразрешимой для $n \leq 3$ . Квадратура $n = 4$ $$\begin{выровнено} \xi_{1,7}&=1.00000000000000000000\\ \xi_{2,6}&=0,85880349620038677732\\ \xi_{3,5}&=0,52084678062073430276\\ \xi_{4}&=0\\ x_{1,7}&=\pm 0,85000000000000000000\\ x_{2,6}&=\pm 0,78770903638639276855\\ x_{3,5}&=\pm 0,61344258003376366028\\ х_{4}&=0\\ w_{1,7}&=0,83593508805857758387\\ w_{2,6}&=-0,88789837944004855297\\ w_{3,5}&=0,74485659488394778770\\ w_{4}&=0,30710669649752318141\\ \end{выровнено} $$
Для $p = 5$
Задача кажется неразрешимой для $n \leq 3$.
Квадратура $n = 4$
$$
\begin{выровнено}
\xi_{1,8}&=1.00000000000000000000\\
\xi_{2,7}&=0,95880851739522516021\\
\xi_{3,6}&=0,86778546156594895262\\
\xi_{4,5}&=0,090906828432672730508\\
x_{1,8}&=\pm 0.
Квадратура $n = 5$ $$ \begin{выровнено} \xi_{1,10}&=1.00000000000000000000\\ \xi_{2,9}&=0,90991052436123162672\\ \xi_{3,8}&=0,67405321511028038136\\ \xi_{4,7}&=0,38251754788591463719\\ \xi_{5,6}&=0,14666023863496339182\\ x_{1,10}&=\pm 0,85000000000000000000\\ x_{2,9}&=\pm 0,81080845694343238659\\ x_{3,8}&=\pm 0,69785632326230130357\\ x_{4,7}&=\pm 0,52570802575914068441\\ x_{5,6}&=\pm 0,32551808308258552196\\ w_{1,10}&=1,8511750976308568442\\ w_{2,9}&=-2,6071695839739403098\\ w_{3,8}&=1,7504677140719977735\\ w_{4,7}&=-0,84051661731816264992\\ w_{5,6}&=0,84604338958924834195\\ \end{выровнено} $$
На всякий случай, если вы хотите воспроизвести результаты, вот мой скрипт Mathematica.
96 \тильда w_j g(x_j)\\
\тильда w_{1,6} = 0,306100114\\
\тильда w_{2,5} = 0,345153691\\
\тильда w_{3,4} = 0,341741013.
$$
Обратите внимание, что эта квадратура не совсем хороша, когда $g(x)$ — полином, но точна, когда $\frac{g(x)}{\omega(x)}$ — полином от 11- степень.
Приложение . Для $n = 10$ тот же метод дает $\sigma \ приблизительно 0,2565088$ и $$ х_{1,10} = \pm 0,85000000\\ х_{2,9} = \pm 0,63553066\\ х_{3,8} = \pm 0,44273486\\ х_{4,7} = \pm 0,26175323\\ х_{5,6} = \pm 0,086652210\\ \тильда w_{1,10} = 0,22829400\\ \тильда w_{2,9} = 0,20160757\\ \тильда w_{3,8} = 0,18564405\\ \тильда w_{4,7} = 0,17726595\\ \тильда w_{5,6} = 0,17359644. $$
Дельта-кванты – Гауссова квадратура
Гауссова квадратура – Гаусс-лежандра Интеграция
- 3,04
- 1
- 2
- 3 9006 4
- 4
- 5
Голосов: 6206
Часто в области количественных финансы, необходимо применить численное интегрирование, чтобы получить цифры риска или оценки, которые в противном случае были бы невозможны, поскольку решения для этих интегрирований в закрытой форме не существуют.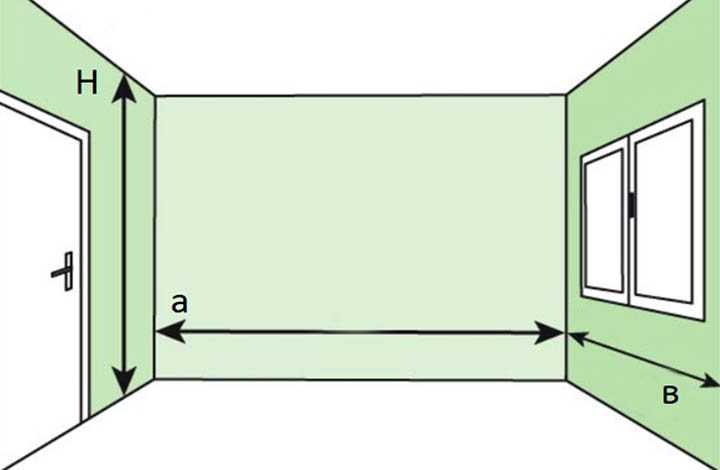
Для этого существует несколько вариантов численных методов. Примеры включают трапецеидальные квадратуры, квадратуры Буля и Гаусса. Квадратура Гаусса, вероятно, является наиболее популярным методом на практике сегодня. Эта статья посвящена интегрированию Гаусса-Ландра, которое применяется для численного вычисления определенных интегралов.
Давайте сначала кратко поговорим о полиномах Лежандра:
Полиномы Лежандра
Рассмотрим рекурсивные уравнения 1 и 2 ниже.
Применяя уравнение 2 для n = 1, получаем 2P2(x) = 3xP 1 (x) — P 0 (x) (3)
Решая (3) имеем ,
Аналогично, для n = 2, получаем 3P 3 (x)=5xP 2 (x)-2P 1 (x) или, 3P 3 (x)=15/2x 2 -5/2x-2x
что ведет к,
Первые пять полиномов Лежандра приведены в таблице ниже. К ним относятся такие методы, как Bisection, Newton, Brent и т. д. Здесь нам, однако, нужна схема для вычисления всех корней этих многочленов Лежандра.
Ниже приведена наводящая на размышления схема:
Предположим, что у нас есть полином Лежандра P(x), нам нужны все корни, такие как P(x) = 0,
1. Найдите первый корень (R 1 ) числа P(x) с помощью решателя (бисекция, Ньютон и т. д.)
3. Используйте решатель, чтобы найти следующий корень (R 2 ).
4. Найдите f'(x) такое, что f'(x) * (x-R 2 ) = f(x) или (x-R 1 ) * (x-R 2 ) * f'(x) = P (х)
Итак, и так далее. n — степень полинома. Это начальное предположение эффективно сходится.
Вычисление f(x) таким образом, что f(x) * (x — R 1 ) = P(x)
Допустим, у нас есть
(1),
(2) 9000 5
(3 )
и нам нужно узнать коэффициенты а 0 , а 1 , а 2 , а 3 … и т.д.
решая (3) получаем,
что упрощается до
, (4)
и, (5)
(6)
2 точки Правило интегрирования Гаусса Лежандра
Два точка Правило интегрирования Гаусса-Лжандра показано в уравнении (7) ниже:
(7)
, где x 1 и x 2 — абсциссы, а w 1 и w 2 — веса для двухточечного правила интегрирования Гаусса-Лжандра.
Абсциссы правила n точек — это корни функции Лежандра степени n. Например, для правила двух точек у нас есть функция Лежандра. Таким образом, корни уравнения P 2 (x) = 0 являются абсциссами двухточечного правила Гаусса-Лжандра.
Далее, корни функции Лежандра степени 2 (см. таблицу 1 выше) таковы, как показано ниже.
(8)
Чтобы найти веса w 1 и w 2 , нам нужны два уравнения соотношения. Поэтому мы используем наше знание определенного интегрирования 1 и x, что дает нам следующие два соотношения.
(9)
или, (10)
(11)
Подставляя (11) в (7) получаем
(12)
Приложение 2 точки Гаусса Правило Лежандра
Пример 1 :
Примем так, чтобы двухточечное приближение Гаусса-Ландра было следующим:
или
, где точное решение равно 0,74682413281243
Пример 2. Вычисление
Правило двух точек приводит к
, так что приближенное решение с использованием правила двух точек равно 900 05
, где точное решение равно ln(3 ) — ln(1) = 1,09861228866811.
Правило интегрирования Гаусса Лежандра по 4 точкам
Абсциссы и веса для правила по 4 точкам следующие:
x1 = -0,339981043584856, x2=-0,861136311594053, x3=0,339981043584856 и x4=0,861136311594053.
w1 = 0,652145154862546, w2 = 0,347854845137454, w3 = 0,652145154862546 и w4 = 0,347854845137454.
Пример 3: Вернемся ко второму примеру, так как нам нужно оценить, используя 4-точечное правило Гаусса Лежандра.
Применяя правило четырех точек, имеем
Подставляя указанные выше значения весов и абсцисс, получаем . Мы замечаем, что правило 4-х баллов дает более близкий результат, чем правило 2-х баллов.
Правило интегрирования Гаусса-Лжандра для N точек
До сих пор мы видели применение правил интегрирования Гаусса-Ландра для 2 и 4 точек. Обобщение для правила интегрирования более высокого порядка выглядит следующим образом: (13)
, где x i s и w i s — абсциссы и веса, применимые для правила N точек.
Таблица для правила Гаусса Лежандра более высокого порядка доступна по ссылке ниже.
Просмотр абсцисс Гаусса Лежандра и весов квадратур Гаусса Лежандра более высокого порядка.
Правило более высокого порядка обычно дает лучшее приближение к требуемому интегрированию. В таблице 2 ниже показано, как улучшаются результаты расчета по мере того, как мы переходим к правилам Гаусса-Лжандра более высокого порядка. Правило 32 или 64 пунктов достаточно для большинства реальных случаев.
| Заказ (н) | Приближение Гаусса Лежандра | Ошибка (%) |
|---|---|---|
| 2 | 1.09090909090909 | 0,70118% |
| 4 | 1.09857035364936 | 0,00382% |
| 8 | 1.09861228751918 | 0,000000105% |
| 16 | 1.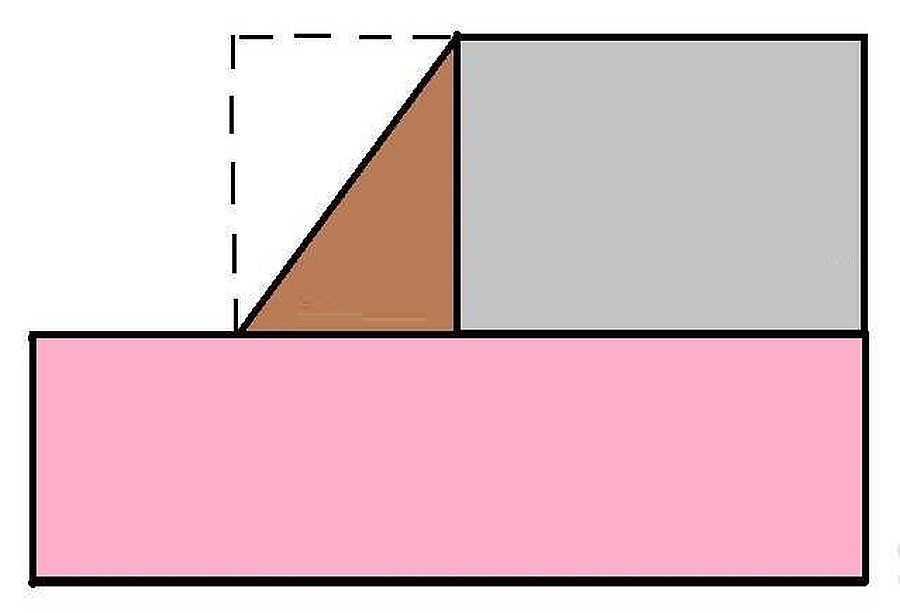 Высчитать квадратуру: Примеры расчетов площади помещения Scroll to top
|